python不同排序算法的比较
1. 冒泡排序:相邻两个数相比较,如果大于则交换顺序,有序区在列表尾部
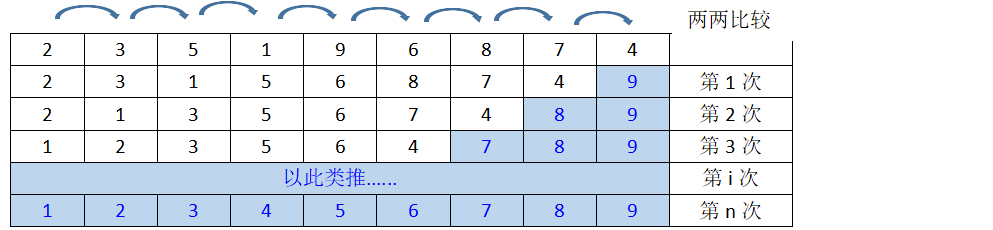
代码实例:
def bubble_sort(li): for i in range(len(li)-1): for j in range(len(li)-i-1): if li[j] > li[j+1]: li[j], li[j+1] = li[j+1], li[j]
时间复杂度为O(N²) 如果遇到中途排序好而不发生变化的列表:[7,8,9,1,2,3,4,5,6] 改进方法: def bubble_sort_better(li): for i in range(len(li)-1): andmark = False for j in range(len(li)-i-1): if li[j] > li[j+1]: li[j], li[j+1] = li[j+1], li[j] andmark = True if not andmark: return 值需要进行三次冒泡即可
2. 选择排序:第i个和后续的元素一一对比,如果小于则交换位置,有序区在列表头部
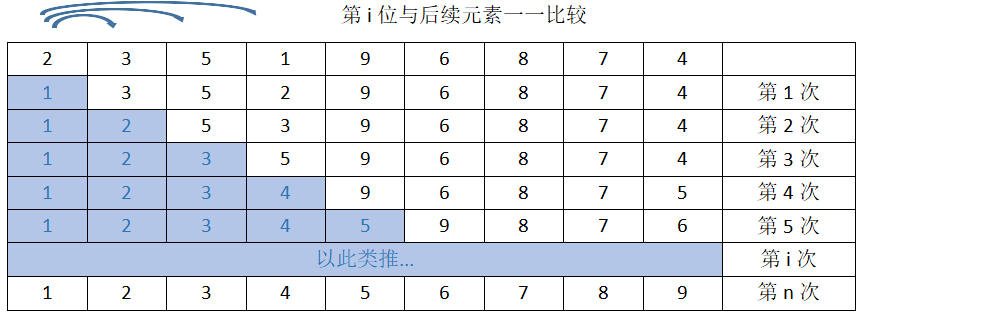
代码实例:
def select_sort(li): for i in range(len(li)-1): for j in range(i+1, len(li)): if li[i] > li[j]: li[i], li[j] = li[j], li[i] 时间复杂度O(N²)
创建新列表存放排序元素
def select_sort_new(li):
new_li = []
for i in range(len(li)):
min_li = min(li) # 遍历一次li
new_li.append(min_li)
li.remove(min_li) # 遍历一次li
return new_li
缺点:创建新的列表,增加空间复杂度,时间复杂度为O(N³)
3. 插入排序:将后续的元素和有序区的元素从右往左比较,大于则不变,小于则插入
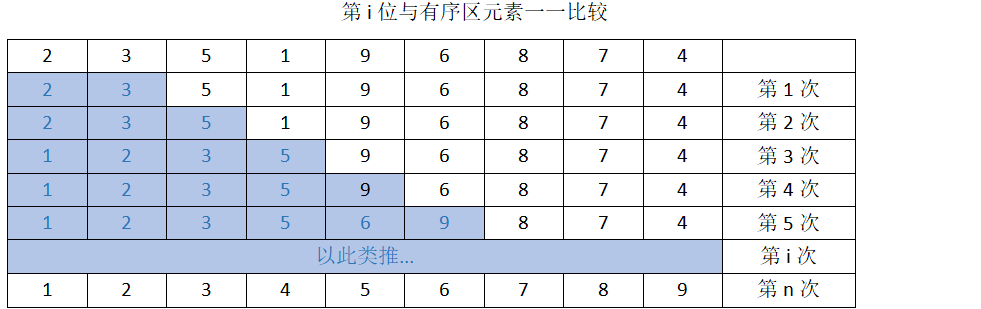
代码示例:
def insert_sort(li): for i in range(1,len(li)): # i 为要插入元素的下标 tem = li[i] # 保存插入元素的值 j = i - 1 # 插入元素的前一个元素 while j >=0 and li[j]>tem: # 当插入元素小于对比元素的时候,则将对比的元素后移 li[j+1] = li[j] j -= 1 # 向比较的元素继续往前移动 li[j+1] = tem # 如果大于对比的元素,则插入后面
时间复杂度为O(N²)
4. 快速排序:将元素把列表分成左右大小两个部分
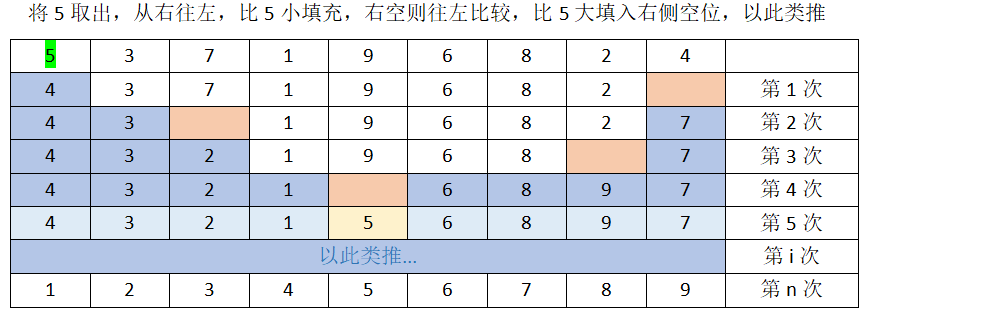
代码示例:
def partion(li, left, right): tem = li[left] # 将左边的元素取出 while left < right: # 如果左边下标小于右边小标,保证中间存在元素 while left < right and li[right] >= tem: right -= 1 li[left] = li[right] # 将右边的的元素放到左边空位置上 while left < right and li[left] <= tem: left += 1 li[right] = li[left] li[left] = tem # 当左右指针相等时,则将原来的数放到这个空位置上 return left # 返回这个分割的元素
# 递归 def quick_sort(li, left, right): if left < right: mid = partion(li, left, right) quick_sort(li, left, mid-1) quick_sort(li, mid+1, right) quick_sort(li, 0, len(li)-1)
时间复杂度为O(NlogN)
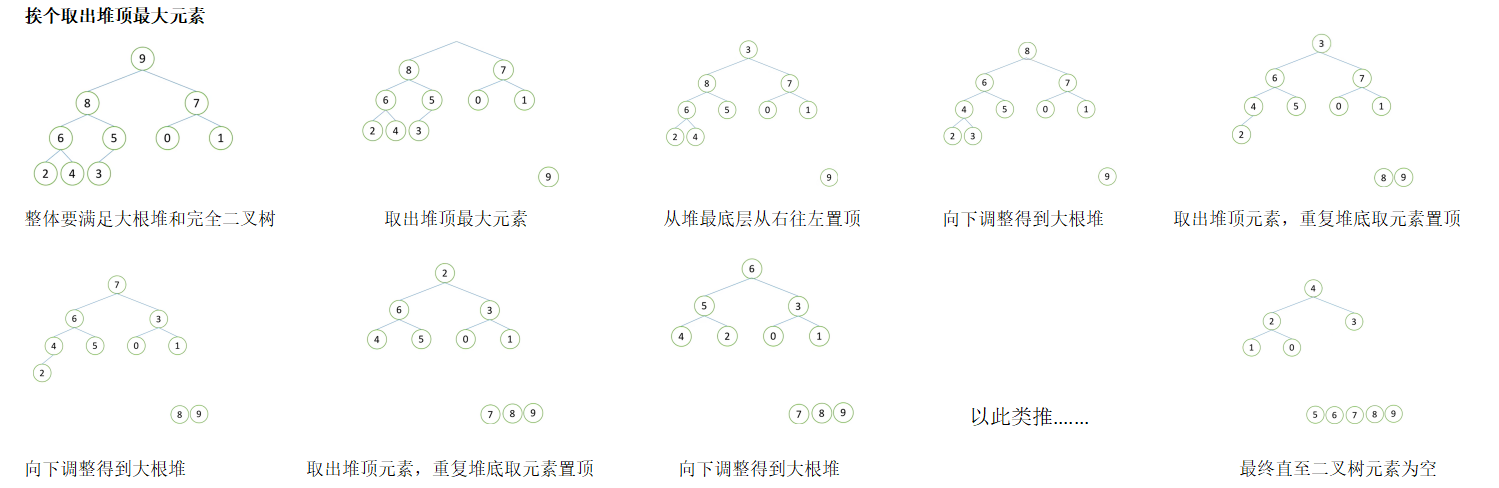
5. 堆排序:先将无序列表建大小根堆,在通过二叉树的算法逐一将最大元素作为根节点取出排序
堆排序的过程:
1. 建立堆
2. 得到堆顶元素为最大元素
3. 去掉堆顶元素,将堆的最后一个元素放置堆顶,通过向下调整得出堆顶元素为第二大元素
4. 重复以上步骤,知道堆元素为空

代码示例:
import random
# 建堆函数
def sift(li, low, end): # li列表,low堆的根节点位置,end堆的最后一个元素位置
i = low # i最开始指向根节点 j = 2 * i + 1 # j为二叉树每层的左孩子 tmp = li[low] # 把堆顶存起来 while j <= end: # 当j位置有元素 if j+1 <= end and li[j+1] > li[j]: # 存在右孩子并且比左孩子大 j = j + 1 # j指向右孩子 if li[j] > tmp # 如果孩子大于堆顶的数 li[i] = li[j] # 堆顶的元素换成j的元素 i = j # 往下走一层 j = 2 * i + 1 # j重新赋值 else: li[i] = tmp # 将取出的值放到对应的空位上 break else: li[i] = tmp # 如果一开始就是最大的,则放原来的位置上 # 堆排序函数 def deap_sort(li): n = len(li) # 建堆过程,i为建堆时需要调整的根的下标,即每层二叉树的父节点 for i in range((n-2)//2, -1, -1): # (n-2)//2为二叉树的每个父节点,倒序到0,第二个-1是因为不包尾 sift(li, i, n-1) print(li) # 堆排序过程 for j in range(n-1, -1 ,-1): # j为li的元素,从后往前开始循环 li[0], li[j] = li[j], li[0] # 第一个元素与最后一个元素交换,将最后一个元素放置堆顶,即取出元素过程 sift(li, 0, j-1) print(li)
li = [i for i in range(100)] random.shuffle(li) heap_sort(li)
时间复杂度为O(NlogN)
# 第三方封装堆排序
import heapq
heapq.heapify(li) # 建堆
lis = []
for i in range(len(li)-1):
lis.append(heapq.heappop(li)) # 每次移除首个最小值元素
6. 归并排序:将列表两两区分,直到元素等于0或1,在进行排序合并


代码示例:
# 归并排序 def merge(li, low, mid, end): i = low j = mid + 1 tmp = [] while i <= mid and j <= end: # 两表都存在数 if li[i] <= li[j]: tmp.append(li[i]) i += 1 else: tmp.append(li[j]) j += 1 while i <= mid: # 左边还存在元素 tmp.append(li[i]) i += 1 while j <= end: # 右边还存在元素 tmp.append(li[j]) j += 1 li[low:end+1] = tmp def merge_sort(li, low, end): if low < end: mid = (low + end) // 2 merge_sort(li, low, mid) merge_sort(li, mid+1, end) merge(li, low, mid, end) import random li = list(range(100)) random.shuffle(li) merge_sort(li, 0, len(li)-1) print(li)
时间复杂度为O(NlogN)
7. 六种排序的比较
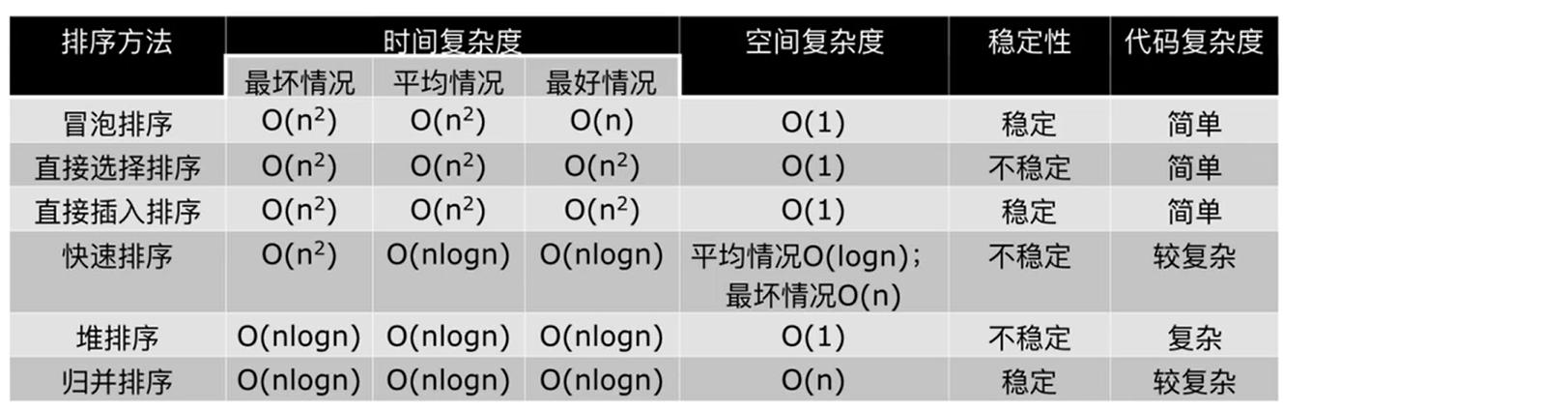
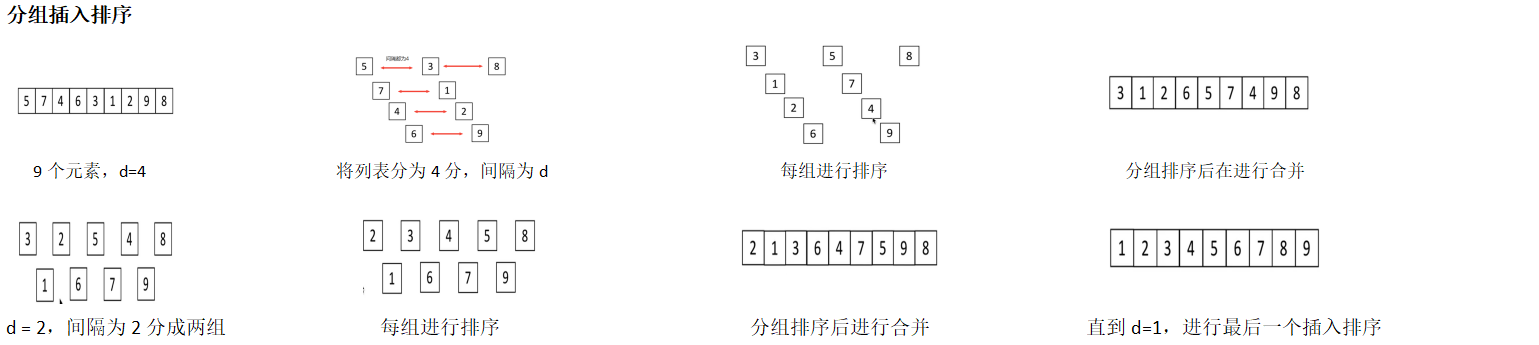
8. 希尔排序:有插入排序变化而来,是一种分组插入排序算法
1. 首先取一个整数d1 = n / 2,将元素分为d1个组,每组相邻量元素之间的距离是d1,在各组内进行排序
2. 取第二个整数d2 = d1 / 2,重复上述分组过程,知道di = 1,即所有元素在同一组内进行直接插入排序
3. 希尔排序每趟并不是使某些元素有序,而是使整体数据变得接近有序,最后一趟排序是的所有数据有序
代码示例:
# 希尔排序 import random def shell_sort(li): d = len(li) // 2 # d的初始值为长度除以2 while d >= 1: for i in range(d, len(li)): # 第一次循环从d往后依次对比 tmp = li[i] # 将第一个对比的数存起来 j = i - d # j为每一组对应的数 while j >= 0 and li[j] > tmp: li[j+d] = li[j] # 大于交换位置 j -= d # 在向前进行比较 li[j+d] = tmp # 否则不变 d //= 2 # 第二次取d值 li = list(range(100)) random.shuffle(li) shell_sort(li)
时间复杂度和选取的d序列有关
9. 计数排序:已知最大范围的列表,对其中的数据进行统计

代码示例:
# 计数排序 def count_sort(li, max_count): count = [0 for _ in range(max_count+1)] # 生成max_count个初始0 for val in li: count[val] += 1 # 遍历计数过程 li.clear() for index, val in enumerate(count): # 获取下标和其对应的值 for i in range(val): li.append(index) # 循环并添加对应下标数量 import random li = [random.randint(0,100) for i in range(1000)] count_sort(li,1000)
时间复杂度为O(N)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号