主成分分析PCA数据降维原理及python应用（葡萄酒案例分析）

主成分分析（PCA）——以葡萄酒数据集分类为例

　　1、认识PCA

　　　　（1）简介

　　　　（2）方法步骤

　　2、提取主成分

　　3、主成分方差可视化

　　4、特征变换

　　5、数据分类结果

　　6、完整代码

　　总结：

1、认识PCA

（1）简介

数据降维的一种方法是通过特征提取实现，主成分分析PCA就是一种无监督数据压缩技术，广泛应用于特征提取和降维。

换言之，PCA技术就是在高维数据中寻找最大方差的方向，将这个方向投影到维度更小的新子空间。例如，将原数据向量x，通过构建 $d\times k$ 维变换矩阵 W，映射到新的k维子空间，通常( $k< < d$ )。

原数据d维向量空间 $\large x=[x_{1},x_{2},...,x_{d}],x\in R^{d}$ 经过 $xW,W\in R^{d\times k}$ ,得到新的k维向量空间 $\large z=[z_{1},z_{2},...,z_{k}],z\in R^{k}$ .

第一主成分有最大的方差，在PCA之前需要对特征进行标准化，保证所有特征在相同尺度下均衡。

（2）方法步骤

标准化d维数据集
构建协方差矩阵。
将协方差矩阵分解为特征向量和特征值。
对特征值进行降序排列，相应的特征向量作为整体降序。
选择k个最大特征值的特征向量， $k< < d$ 。
根据提取的k个特征向量构造投影矩阵 $\large W$ 。
d维数据经过 $\large W$ 变换获得k维。

下面使用python逐步完成葡萄酒的PCA案例。

2、提取主成分

下载葡萄酒数据集wine.data到本地，或者到时在加载数据代码是从远程服务器获取，为了避免加载超时推荐下载本地数据集。

来看看数据集长什么样子！一共有3类，标签为1,2,3 。每一行为一组数据，由13个维度的值表示，我们将它看成一个向量。

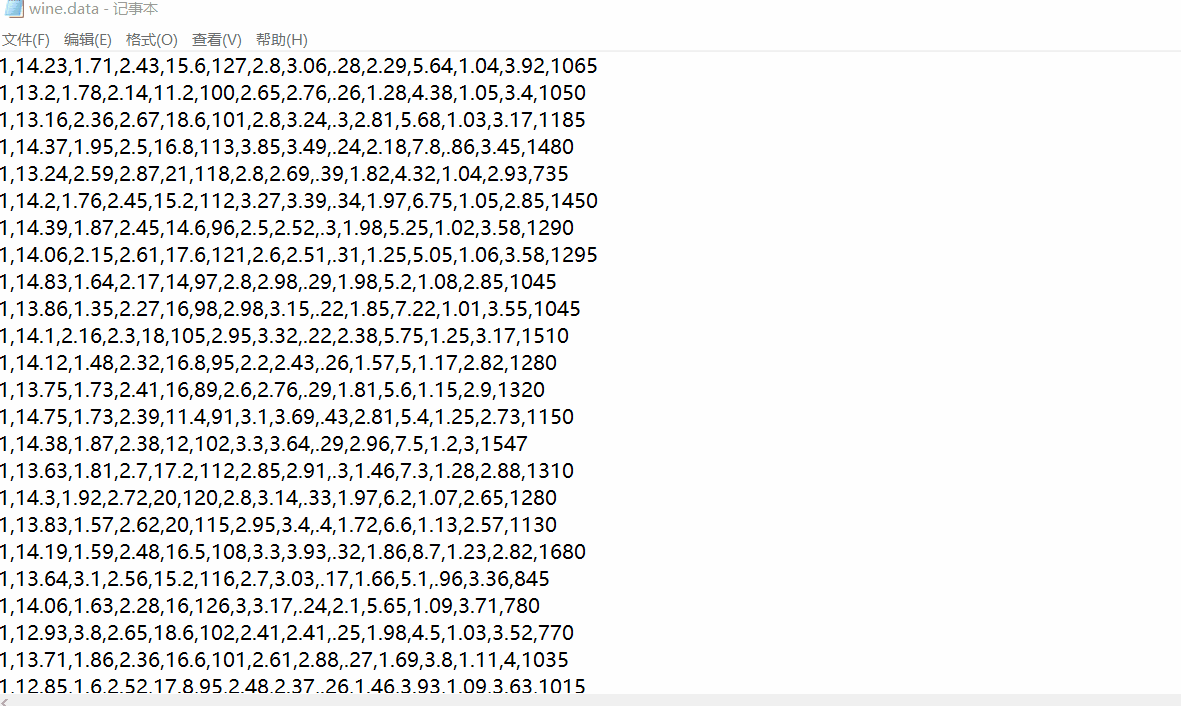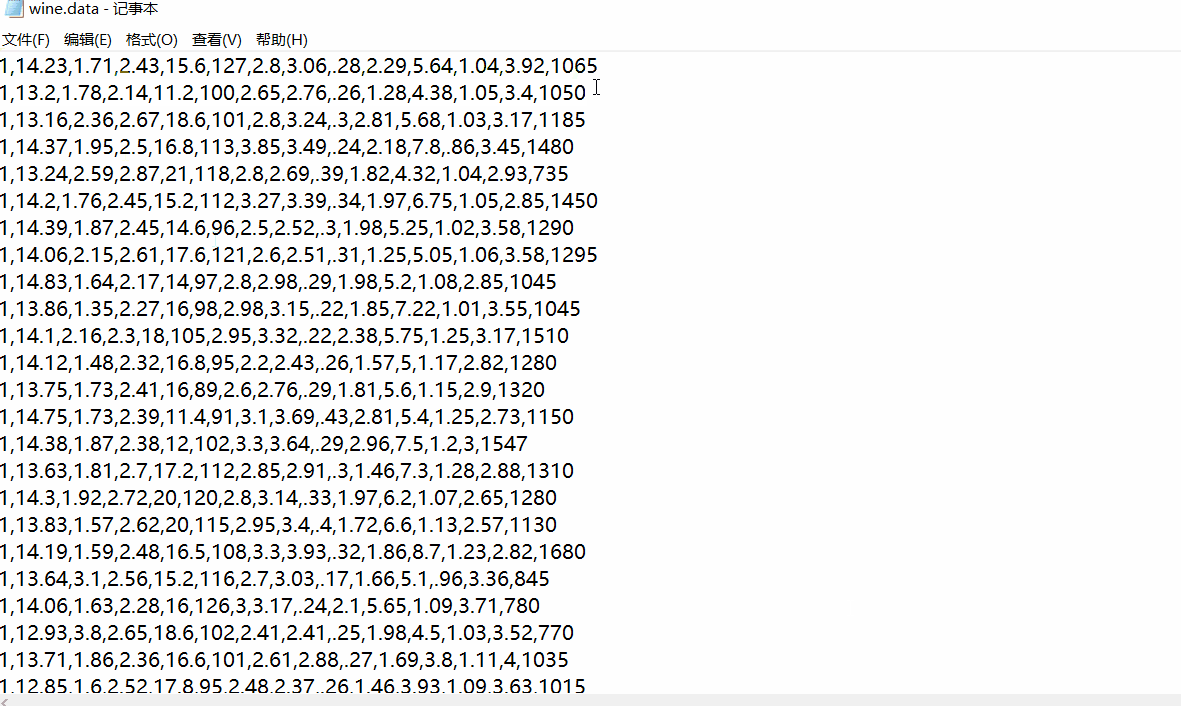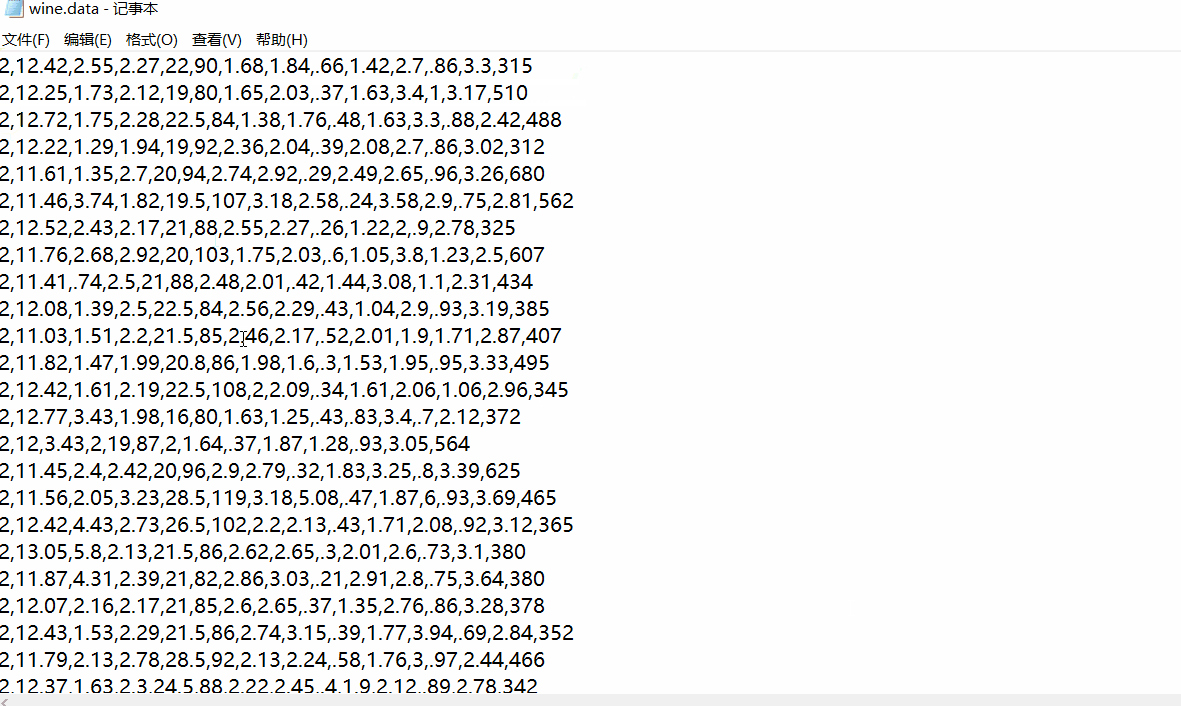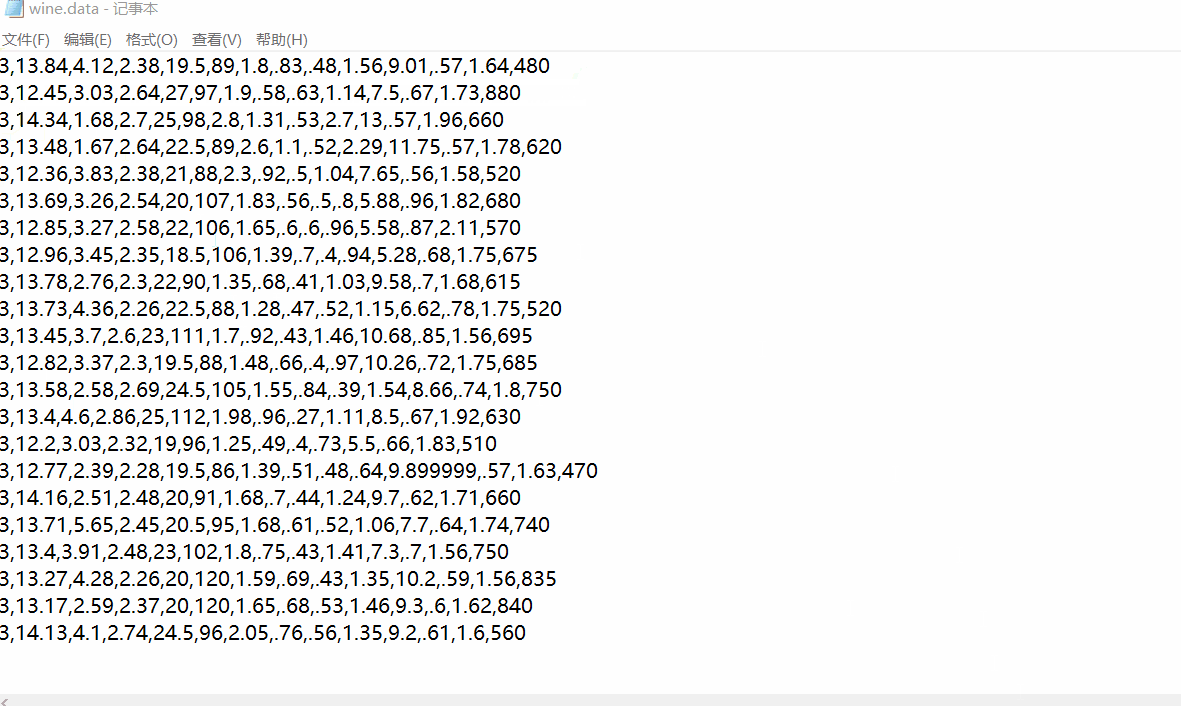
开始加载数据集。

import pandas as pd
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
 
 
# load data
df_wine = pd.read_csv('D:\\PyCharm_Project\\maching_learning\\wine_data\\wine.data', header=None)  # 本地加载，路径为本地数据集存放位置
# df_wine=pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data',header=None)#服务器加载

下一步将数据按7:3划分为training-data和testing-data，并进行标准化处理。

# split the data，train：test=7:3
x, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, stratify=y, random_state=0)
 
# standardize the feature 标准化
sc = StandardScaler()
x_train_std = sc.fit_transform(x_train)
x_test_std = sc.fit_transform(x_test)

这个过程可以自行打印出数据进行观察研究。

接下来构造协方差矩阵。 $\large d\times d$ 维协方差对称矩阵，实际操作就是计算不同特征列之间的协方差。公式如下：

$\LARGE \sigma _{jk}=\frac{1}{n}\sum_{i=1}^{n}(x_{j}^{(i)}-\mu _{j})(x_{k}^{(i)}-\mu _{k})$

公式中，jk就是在矩阵中的行列下标，i表示第i行数据， $\mu_{j},\mu_{k}$ 分别为特征列 j，k的均值。最后得到的协方差矩阵是13*13，这里以3*3为例，如下：

$\sum =\begin{bmatrix} \sigma _{1}^{2} \sigma _{12} \sigma _{13}\\ \sigma _{21} \sigma _{2}^{2} \sigma _{23}\\ \sigma _{31} \sigma _{32} \sigma _{3}^{2} \end{bmatrix}$

下面使用numpy实现计算协方差并提取特征值和特征向量。

# 构造协方差矩阵，得到特征向量和特征值
cov_matrix = np.cov(x_train_std.T)
eigen_val, eigen_vec = np.linalg.eig(cov_matrix)
# print("values\n ", eigen_val, "\nvector\n ", eigen_vec)# 可以打印看看

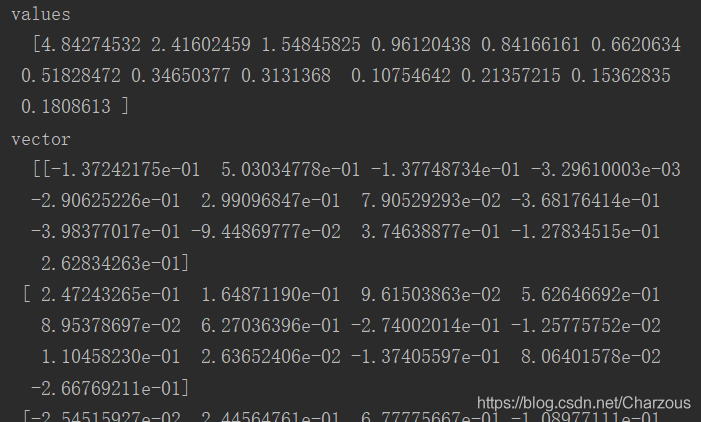
3、主成分方差可视化

首先，计算主成分方差比率，每个特征值方差与特征值方差总和之比：

$\LARGE \frac{\lambda _{j}}{\sum_{j=1}^{d}\lambda _{j}}$

代码实现：

# 解释方差比
tot = sum(eigen_val)  # 总特征值和
var_exp = [(i / tot) for i in sorted(eigen_val, reverse=True)]  # 计算解释方差比，降序
# print(var_exp)
cum_var_exp = np.cumsum(var_exp)  # 累加方差比率
plt.rcParams['font.sans-serif'] = ['SimHei']  # 显示中文
plt.bar(range(1, 14), var_exp, alpha=0.5, align='center', label='独立解释方差')  # 柱状 Individual_explained_variance
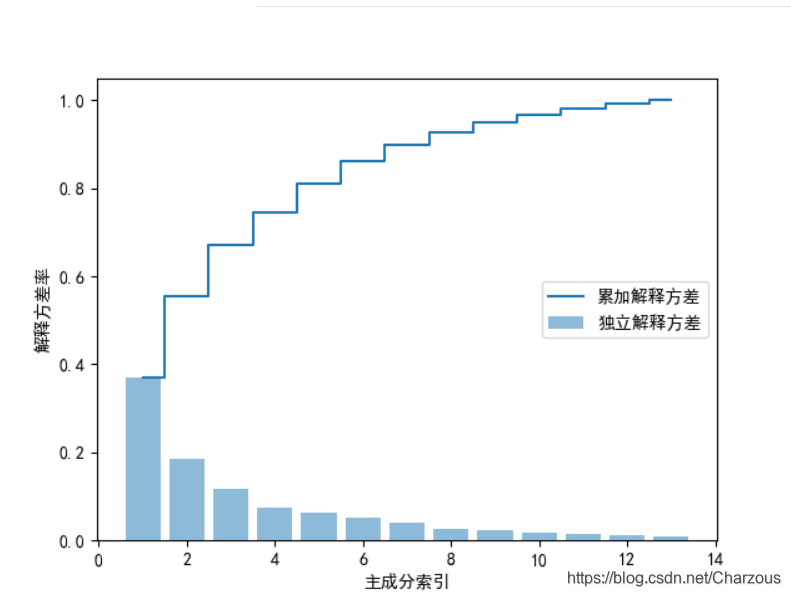
plt.step(range(1, 14), cum_var_exp, where='mid', label='累加解释方差')  # Cumulative_explained_variance
plt.ylabel("解释方差率")
plt.xlabel("主成分索引")
plt.legend(loc='right')
plt.show()

可视化结果看出，第一二主成分占据大部分方差，接近60%。

4、特征变换

这一步需要构造之前讲到的投影矩阵 $\large W$ ，从高维d变换到低维空间k。

先将提取的特征对进行降序排列：

# 特征变换
eigen_pairs = [(np.abs(eigen_val[i]), eigen_vec[:, i]) for i in range(len(eigen_val))]
eigen_pairs.sort(key=lambda k: k[0], reverse=True)  # (特征值，特征向量)降序排列

从上步骤可视化，选取第一二主成分作为最大特征向量进行构造投影矩阵。

w = np.hstack((eigen_pairs[0][1][:, np.newaxis], eigen_pairs[1][1][:, np.newaxis]))  # 降维投影矩阵W

13*2维矩阵如下：

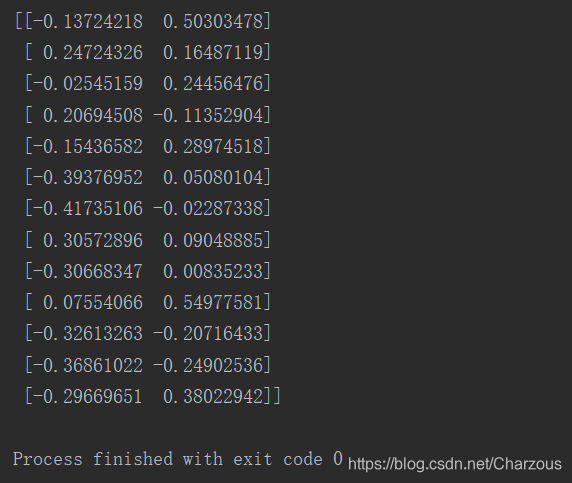
这时，将原数据矩阵与投影矩阵相乘，转化为只有两个最大的特征主成分。

x_train_pca = x_train_std.dot(w)

5、数据分类结果

使用 matplotlib进行画图可视化，可见得，数据分布更多在x轴方向（第一主成分），这与之前方差占比解释一致，这时可以很直观区别3种不同类别。

代码实现：

color = ['r', 'g', 'b']
marker = ['s', 'x', 'o']
for l, c, m in zip(np.unique(y_train), color, marker):
    plt.scatter(x_train_pca[y_train == l, 0],
                x_train_pca[y_train == l, 1],
                c=c, label=l, marker=m)
plt.title('Result')
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.legend(loc='lower left')
plt.show()

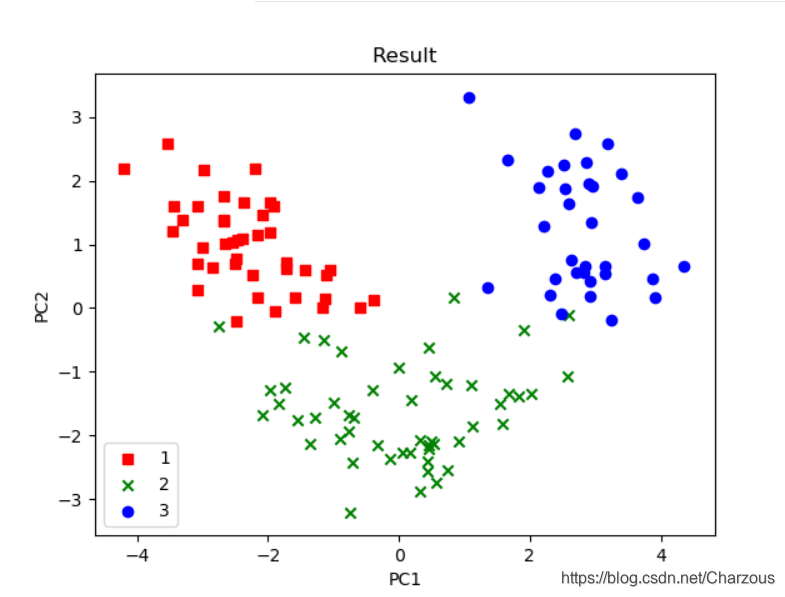
本案例介绍PCA单个步骤和实现过程，一点很重要，PCA是无监督学习技术，它的分类没有使用到样本标签，上面之所以看出3类不同标签，是后来画图时候自行添加的类别区分标签。

6、完整代码

import pandas as pd
import numpy as np
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
 
 
def main():
    # load data
    df_wine = pd.read_csv('D:\\PyCharm_Project\\maching_learning\\wine_data\\wine.data', header=None)  # 本地加载
    # df_wine=pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data',header=None)#服务器加载
 
    # split the data，train：test=7:3
    x, y = df_wine.iloc[:, 1:].values, df_wine.iloc[:, 0].values
    x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, stratify=y, random_state=0)
 
    # standardize the feature 标准化单位方差
    sc = StandardScaler()
    x_train_std = sc.fit_transform(x_train)
    x_test_std = sc.fit_transform(x_test)
    # print(x_train_std)
 
    # 构造协方差矩阵，得到特征向量和特征值
    cov_matrix = np.cov(x_train_std.T)
    eigen_val, eigen_vec = np.linalg.eig(cov_matrix)
    # print("values\n ", eigen_val, "\nvector\n ", eigen_vec)
 
    # 解释方差比
    tot = sum(eigen_val)  # 总特征值和
    var_exp = [(i / tot) for i in sorted(eigen_val, reverse=True)]  # 计算解释方差比，降序
    # print(var_exp)
    # cum_var_exp = np.cumsum(var_exp)  # 累加方差比率
    # plt.rcParams['font.sans-serif'] = ['SimHei']  # 显示中文
    # plt.bar(range(1, 14), var_exp, alpha=0.5, align='center', label='独立解释方差')  # 柱状 Individual_explained_variance
    # plt.step(range(1, 14), cum_var_exp, where='mid', label='累加解释方差')  # Cumulative_explained_variance
    # plt.ylabel("解释方差率")
    # plt.xlabel("主成分索引")
    # plt.legend(loc='right')
    # plt.show()
 
    # 特征变换
    eigen_pairs = [(np.abs(eigen_val[i]), eigen_vec[:, i]) for i in range(len(eigen_val))]
    eigen_pairs.sort(key=lambda k: k[0], reverse=True)  # (特征值，特征向量)降序排列
    # print(eigen_pairs)
    w = np.hstack((eigen_pairs[0][1][:, np.newaxis], eigen_pairs[1][1][:, np.newaxis]))  # 降维投影矩阵W
    # print(w)
    x_train_pca = x_train_std.dot(w)
    # print(x_train_pca)
    color = ['r', 'g', 'b']
    marker = ['s', 'x', 'o']
    for l, c, m in zip(np.unique(y_train), color, marker):
        plt.scatter(x_train_pca[y_train == l, 0],
                    x_train_pca[y_train == l, 1],
                    c=c, label=l, marker=m)
    plt.title('Result')
    plt.xlabel('PC1')
    plt.ylabel('PC2')
    plt.legend(loc='lower left')
    plt.show()
 
 
if __name__ == '__main__':
    main()

View Code

总结：

本案例介绍PCA步骤和实现过程，单步进行是我更理解PCA内部实行的过程，主成分分析PCA作为一种无监督数据压缩技术，学习之后更好掌握数据特征提取和降维的实现方法。记录学习过程，不仅能让自己更好的理解知识，而且能与大家共勉，希望我们都能有所帮助！

我的博客园：https://www.cnblogs.com/chenzhenhong/p/13472460.html

我的CSDN：原创 PCA数据降维原理及python应用（葡萄酒案例分析）

本文链接：https://blog.csdn.net/Charzous/article/details/107883679

posted @ 2020-08-10 22:03 Charzueus 阅读(9969) 评论(0) 编辑收藏举报

刷新页面返回顶部

书山有路===学海无涯

主成分分析PCA数据降维原理及python应用（葡萄酒案例分析）

1、认识PCA

（1）简介

（2）方法步骤

2、提取主成分

3、主成分方差可视化

4、特征变换

5、数据分类结果

6、完整代码

总结：

公告