学习js数据结构与算法—递归

“要理解递归，首先要理解递归。”

递归通常涉及函数调用自身。

每个递归函数都必须有基线条件，即一个不再递归调用的条件（停止点），以防止无限递归。

1.阶乘

n! = n * (n-1) * (n -2) .... * 2 * 1

迭代阶乘

function factorialIterative(n) {
    if (n < 0){
        return undefined;
    }
    let cur = 1
    for (let i = n; i > 1; i--){
        cur = i * cur;
    }
    return cur
}

递归阶乘

function factorialIterative(n) {
    if (n < 0){
        return undefined;
    }
    if (n < 3){
        return n
    }
    return n * factorialIterative(n-1)
}

2.斐波那契数列

0、1、1、2、3、5、8、13、21、34 ......

迭代求斐波那契数列

function fibonacciIterative(n){
    if(n < 1){
        return 0
    }
    if(n < 2){
        return 1
    }
    let fib1 = 0;
    let fib2 = 1;
    for(let i = 2; i <= n; i++){
        cur = fib1 + fib2;
        fib1 = fib2;
        fib2 = cur
    }
    return cur
}

递归求斐波那契数列

function fibonacciIterative(n){
    if(n < 1){
        return 0
    }
    if(n < 2){
        return 1
    }
    return fibonacciIterative(n-1) + fibonacciIterative(n-2)
}

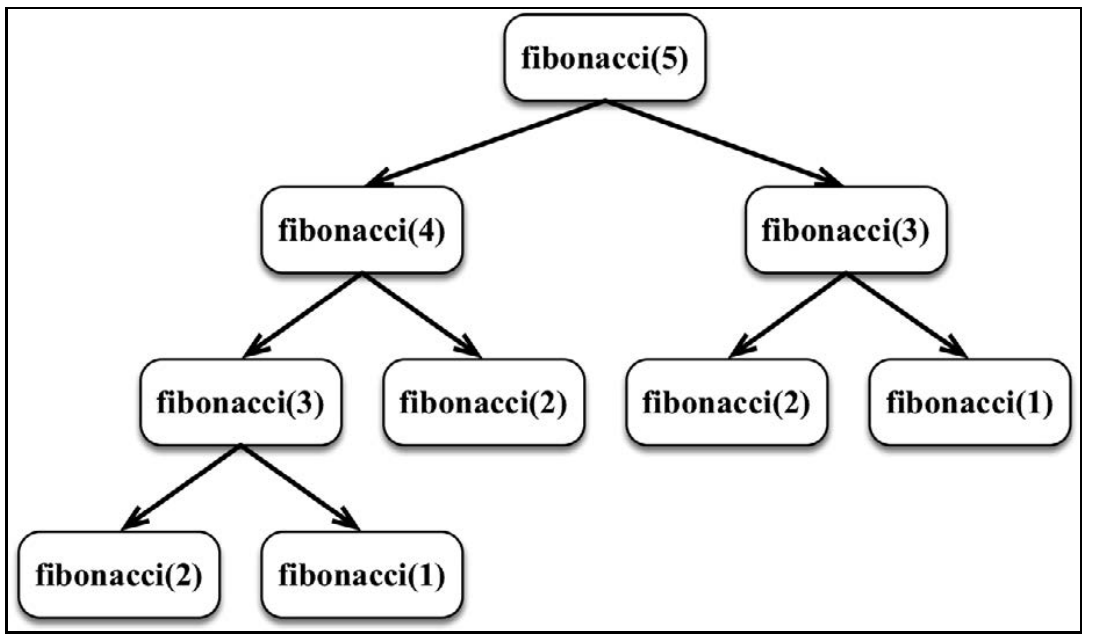
在计算 fibonacci(5)时的调用，会发现 fibonacci(3) 被计算了两次，因此可以将它的结果存储下来，这样当需要再次计算它的时候，就已经有它的结果了。这种做法叫记忆化。记忆化是一种保存前一个结果的值的优化技术，类似于缓存。

记忆化斐波那契数列

function fibonacciMemoization(n) { 
    const memo = [0, 1]; // 声明了一个 memo 数组来缓存所有的计算结果
    const fibonacci = (n) => {
        if (memo[n] != null){ 
            return memo[n]; // 如果结果已经被计算了,就返回它
        }
        return memo[n] = fibonacci(n - 1, memo) + fibonacci(n - 2, memo); // 否则计算该结果并将它加入缓存
    }; 
    return fibonacci; 
}

记忆化方法可以防止递归算法重复计算一个相同的值。