adaboost的样本权重和学习器权重+更新的理解

参考：https://www.bilibili.com/video/BV1x44y1r7Zc/?p=3&spm_id_from=pageDriver&vd_source=bdbb5be671dc7bcfadbe64bf3d0d2f95

 

adaboost有2个权重：样本权重和学习器权重，他们不是一个概念。

样本权重w：

假设甲乙丙三个样本，一开始权重都是1/3，假设他们的输出是1,1,-1; 那么总的输出是(1/3)*(1+1-1)=1/3;是大于0的，学习器1号判断正确类；

但如果他们权重是1/6,1/6,4/6的话，那么总的输出是(1/6)*1+(1/6)*1-(4/6)*1=-(2/6);是小于0的，学习器1号判断错误类；

所以改变样本权重并不是想象中的那样改变样本数量，而是乘以一个权重系数。

 

学习器权重a：

假设还是同一个样本，学习器1号分类为正确类，现在还有学习器2号,3号，分别分类正确，错误；

假设他们一开始的学习器权重都是1/3,那么结果就是1/3*(正确+正确+错误)，整体分类为正确

如果他们学习器权重是1/6,1/6,4/6的话，那么结果就是(1/6)*正确+(1/6)*正确+(4/6)*错误，整体分类为错误；

 

小结：可以看到他们2个原理是一致的，只是权重对象不同，这里用分类举例，但同样可以应用到回归问题中；

 

后面介绍关键的样本权重和学习器权重是如何根据结果更新的问题,直接引用别人的图和公式

学习器权重a更新，这个公式简单一些：

 

 

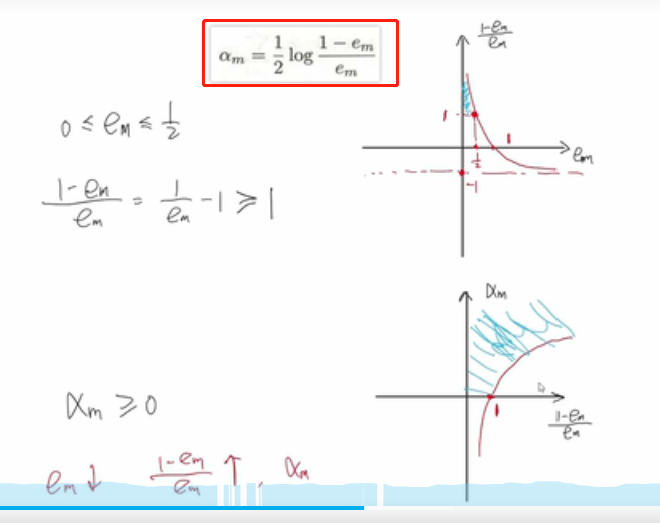
 你的学习器1，2，3根据样本分别判断为正确，正确，错误，但是实际值为正确，错误，错误，其中第二个判断错了，那么误差率e=1/3

这里如果分错2个，则误差率e=2/3 ，如果e大于0.5，就像一个人买股票一买就跌，一卖就涨，失败率2/3,那干脆把这个人当反向指标，他买我就卖，他卖我就买，获得一个1/3失败率的模型，所以这里0<=e<=1/2， 最后根据上图可以简单的推出学习器权重a随着误差率的降低而提高，当e极小的时候，(1-e)/e 会很大，所以加个log限定一下大小。

假设(1-e)/e=100，那么(1/2)*log100=5, 可以看出学习器权重a是可能大于1的，并不是直观上想的那样所有学习器权重a加和为1

 

样本权重w的更新：这个公式复杂一些

 

 

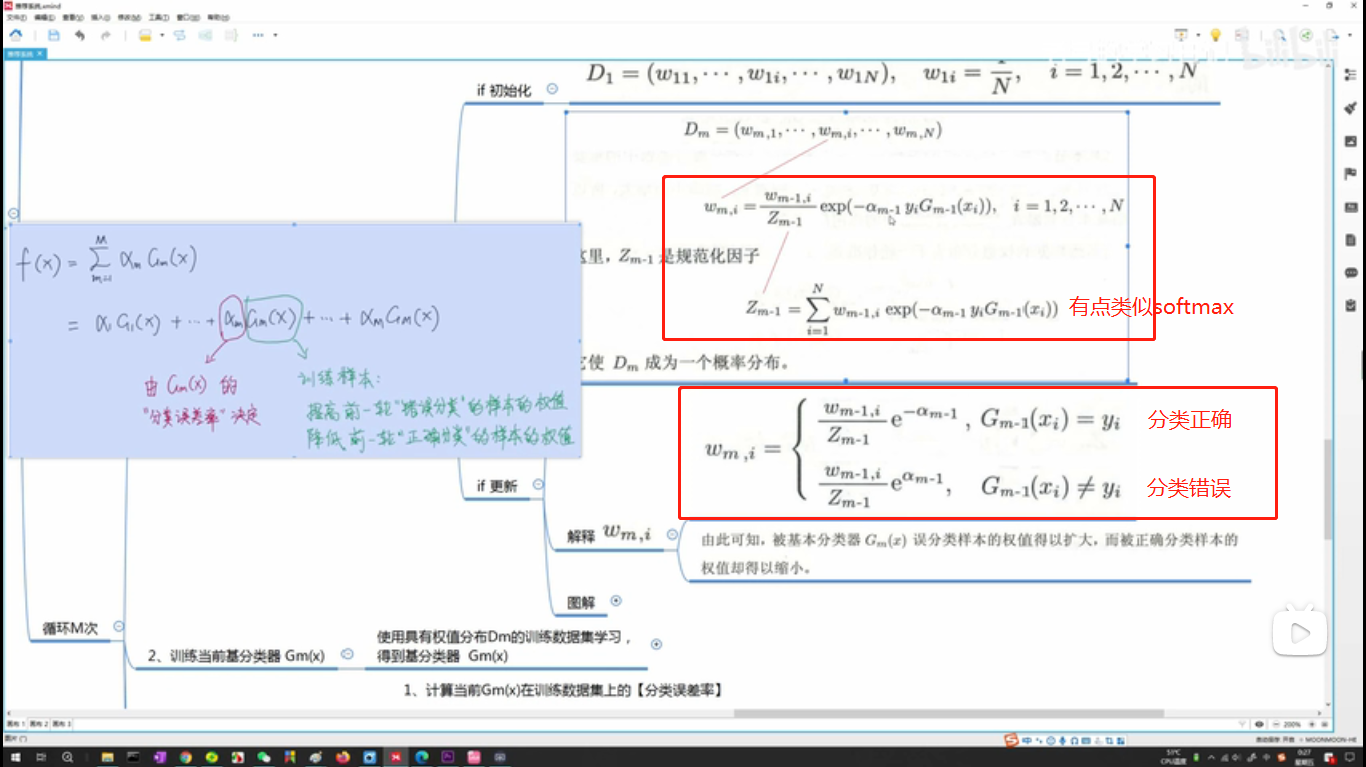
 假设甲乙2个样本，初始化权重1/2, 1/2, 在学习器1号中，甲样本分类正确，乙分类错误，那么我们的目的肯定是增加乙的样本权重，减小甲的，来让后面的学习器2号接着学，那怎么做到的？

公式里的alpha就是这里的a，作为一个学习器权重先不看，不影响性质

准备给学习器2号用的样本权重Wt+1

学习器1号已经用过的样本权重Wt

分类正确就是Wt* e ^ -1

分类错误就是Wt* e ^ 1

 

用上面甲乙的例子：甲乙开始是0.5,0.5，甲分对了，乙分错了

W甲t+1=（权重甲* e ^ -1)/(权重甲* e ^ -1+权重乙* e ^ 1)=（0.5* e ^ -1)/(0.5* e ^ -1+0.5* e ^ 1)=0.12

W乙t+1=（权重乙* e ^ 1)/(权重甲* e ^ -1+权重乙* e ^ 1)=（0.5* e ^ -1)/(0.5* e ^ -1+0.5* e ^ 1)=0.88

可以看见甲分对了，那么样本权重就从0.5降低为0.12，分对了学习器二号就少关注些，乙相反

样本的权重由于公式分母一致，都是规范化因子，所以权重加和为1