BAT机器学习面试1000题系列(36-40题)
BAT机器学习面试1000题系列(36-40题)
36.熵、联合熵、条件熵、相对熵、互信息的定义
为了更好的理解,需要了解的概率必备知识有:
1.大写字母X表示随机变量,小写字母x表示随机变量X的某个具体的取值;
2.P(X)表示随机变量X的概率分布,P(X,Y)表示随机变量X、Y的联合概率分布,P(Y|X)表示已知随机变量X的情况下随机变量Y的条件概率分布;
3.p(X = x)表示随机变量X取某个具体值的概率,简记为p(x);
4.p(X = x, Y = y) 表示联合概率,简记为p(x,y),p(Y = y|X = x)表示条件概率,简记为p(y|x),且有:p(x,y) = p(x) * p(y|x)。
熵:如果一个随机变量X的可能取值为X = {x1, x2,…, xk},其概率分布为P(X = xi) = pi(i = 1,2, ..., n),则随机变量X的熵定义为:
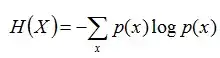
把最前面的负号放到最后,便成了:
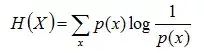
上面两个熵的公式,无论用哪个都行,而且两者等价,一个意思(这两个公式在下文中都会用到)。
联合熵:两个随机变量X,Y的联合分布,可以形成联合熵Joint Entropy,用H(X,Y)表示。
条件熵:在随机变量X发生的前提下,随机变量Y发生所新带来的熵定义为Y的条件熵,用H(Y|X)表示,用来衡量在已知随机变量X的条件下随机变量Y的不确定性。
且有此式子成立:H(Y|X) = H(X,Y) – H(X),整个式子表示(X,Y)发生所包含的熵减去X单独发生包含的熵。至于怎么得来的请看推导:

简单解释下上面的推导过程。整个式子共6行,其中
第二行推到第三行的依据是边缘分布p(x)等于联合分布p(x,y)的和;
第三行推到第四行的依据是把公因子logp(x)乘进去,然后把x,y写在一起;
第四行推到第五行的依据是:因为两个sigma都有p(x,y),故提取公因子p(x,y)放到外边,然后把里边的-(log p(x,y) - log p(x))写成- log (p(x,y)/p(x) ) ;
第五行推到第六行的依据是:p(x,y) = p(x) * p(y|x),故p(x,y) / p(x) = p(y|x)。
相对熵:又称互熵,鉴别信息,Kullback熵,Kullback-Leible散度等。设p(x)、q(x)是X中取值的两个概率分布,则p对q的相对熵是:

在一定程度上,相对熵可以度量两个随机变量的“距离”,且有D(p||q) ≠D(q||p)。另外,值得一提的是,D(p||q)是必然大于等于0的。
互信息:两个随机变量X,Y的互信息定义为X,Y的联合分布和各自独立分布乘积的相对熵,用I(X,Y)表示:

且有I(X,Y)=D(P(X,Y) || P(X)P(Y))。下面,咱们来计算下H(Y)-I(X,Y)的结果,如下:

通过上面的计算过程,我们发现竟然有H(Y)-I(X,Y) = H(Y|X)。故通过条件熵的定义,有:H(Y|X) = H(X,Y) - H(X),而根据互信息定义展开得到H(Y|X) = H(Y) - I(X,Y),把前者跟后者结合起来,便有I(X,Y)= H(X) + H(Y) - H(X,Y),此结论被多数文献作为互信息的定义。更多请查看http://blog.csdn.net/v_july_v/article/details/40508465
37.什么是最大熵
熵是随机变量不确定性的度量,不确定性越大,熵值越大;若随机变量退化成定值,熵为0。如果没有外界干扰,随机变量总是趋向于无序,在经过足够时间的稳定演化,它应该能够达到的最大程度的熵。
为了准确的估计随机变量的状态,我们一般习惯性最大化熵,认为在所有可能的概率模型(分布)的集合中,熵最大的模型是最好的模型。换言之,在已知部分知识的前提下,关于未知分布最合理的推断就是符合已知知识最不确定或最随机的推断,其原则是承认已知事物(知识),且对未知事物不做任何假设,没有任何偏见。
例如,投掷一个骰子,如果问"每个面朝上的概率分别是多少",你会说是等概率,即各点出现的概率均为1/6。因为对这个"一无所知"的色子,什么都不确定,而假定它每一个朝上概率均等则是最合理的做法。从投资的角度来看,这是风险最小的做法,而从信息论的角度讲,就是保留了最大的不确定性,也就是说让熵达到最大。
3.1 无偏原则
下面再举个大多数有关最大熵模型的文章中都喜欢举的一个例子。
例如,一篇文章中出现了“学习”这个词,那这个词是主语、谓语、还是宾语呢?换言之,已知“学习”可能是动词,也可能是名词,故“学习”可以被标为主语、谓语、宾语、定语等等。
令x1表示“学习”被标为名词, x2表示“学习”被标为动词。
令y1表示“学习”被标为主语, y2表示被标为谓语, y3表示宾语, y4表示定语。
且这些概率值加起来的和必为1,即

,

, 则根据无偏原则,认为这个分布中取各个值的概率是相等的,故得到:


因为没有任何的先验知识,所以这种判断是合理的。如果有了一定的先验知识呢?
即进一步,若已知:“学习”被标为定语的可能性很小,只有0.05,即

,剩下的依然根据无偏原则,可得:


再进一步,当“学习”被标作名词x1的时候,它被标作谓语y2的概率为0.95,即

,此时仍然需要坚持无偏见原则,使得概率分布尽量平均。但怎么样才能得到尽量无偏见的分布?
实践经验和理论计算都告诉我们,在完全无约束状态下,均匀分布等价于熵最大(有约束的情况下,不一定是概率相等的均匀分布。 比如,给定均值和方差,熵最大的分布就变成了正态分布 )。
于是,问题便转化为了:计算X和Y的分布,使得H(Y|X)达到最大值,并且满足下述条件:

因此,也就引出了最大熵模型的本质,它要解决的问题就是已知X,计算Y的概率,且尽可能让H(Y|X)最大(实践中,X可能是某单词的上下文信息,Y是该单词翻译成me,I,us、we的各自概率),从而根据已有信息,尽可能最准确的推测未知信息,这就是最大熵模型所要解决的问题。
相当于已知X,计算Y的的概率,转换成公式,便是要最大化下述式子H(Y|X):

且满足以下4个约束条件:

38.简单说下有监督学习和无监督学习的区别 有监督学习:对具有标记的训练样本进行学习,以尽可能对训练样本集外的数据进行分类预测。(LR,SVM,BP,RF,GBDT)
无监督学习:对未标记的样本进行训练学习,比发现这些样本中的结构知识。(KMeans,DL)
39.了解正则化么 正则化是针对过拟合而提出的,以为在求解模型最优的是一般优化最小的经验风险,现在在该经验风险上加入模型复杂度这一项(正则化项是模型参数向量的范数),并使用一个rate比率来权衡模型复杂度与以往经验风险的权重,如果模型复杂度越高,结构化的经验风险会越大,现在的目标就变为了结构经验风险的最优化,可以防止模型训练过度复杂,有效的降低过拟合的风险。
奥卡姆剃刀原理,能够很好的解释已知数据并且十分简单才是最好的模型。
40.协方差和相关性有什么区别? 相关性是协方差的标准化格式。协方差本身很难做比较。例如:如果我们计算工资($)和年龄(岁)的协方差,因为这两个变量有不同的度量,所以我们会得到不能做比较的不同的协方差。为了解决这个问题,我们计算相关性来得到一个介于-1和1之间的值,就可以忽略它们各自不同的度量。







 浙公网安备 33010602011771号
浙公网安备 33010602011771号
还没有评论