笔记(2)[算法]

数据结构与算法的关系

两种算法的比较

计算1-100的结果程序

# 计算0-100的和
sum = 0
for i in range(101):
    sum += i

print(sum)

package main

import "fmt"

func main() {
    sum := 0
    for i :=0; i < 101; i++ {
        sum += i
    }
    fmt.Println(sum)
}

但是!!!18世纪的天才高斯小学就想出来了好办法

n = 100
sum = (1+n) * n / 2
print(sum)

 算法时间复杂度

算法时间复杂度定义

　　在进行算法分析时, 语句的总的执行次数T(n)是关于问题规模n的函数, 进而分析T(n)随着n的变化情况并确定T(n)的数量级. 算法的时间复杂度, 也就是算法的时间量度, 记作: T(n) = O(f(n)). 它表示随问题规模n的增大, 算法执行时间的增长率和f(n)的增长率相同, 称作算法的渐进时间复杂度, 简称为时间复杂度度.其中f(n)是问题规模n的某个函数.

用O()来体现算法时间复杂度的记法.

一般情况下，随着 n 的增大， T(n)增长最慢的算法为最优算法。

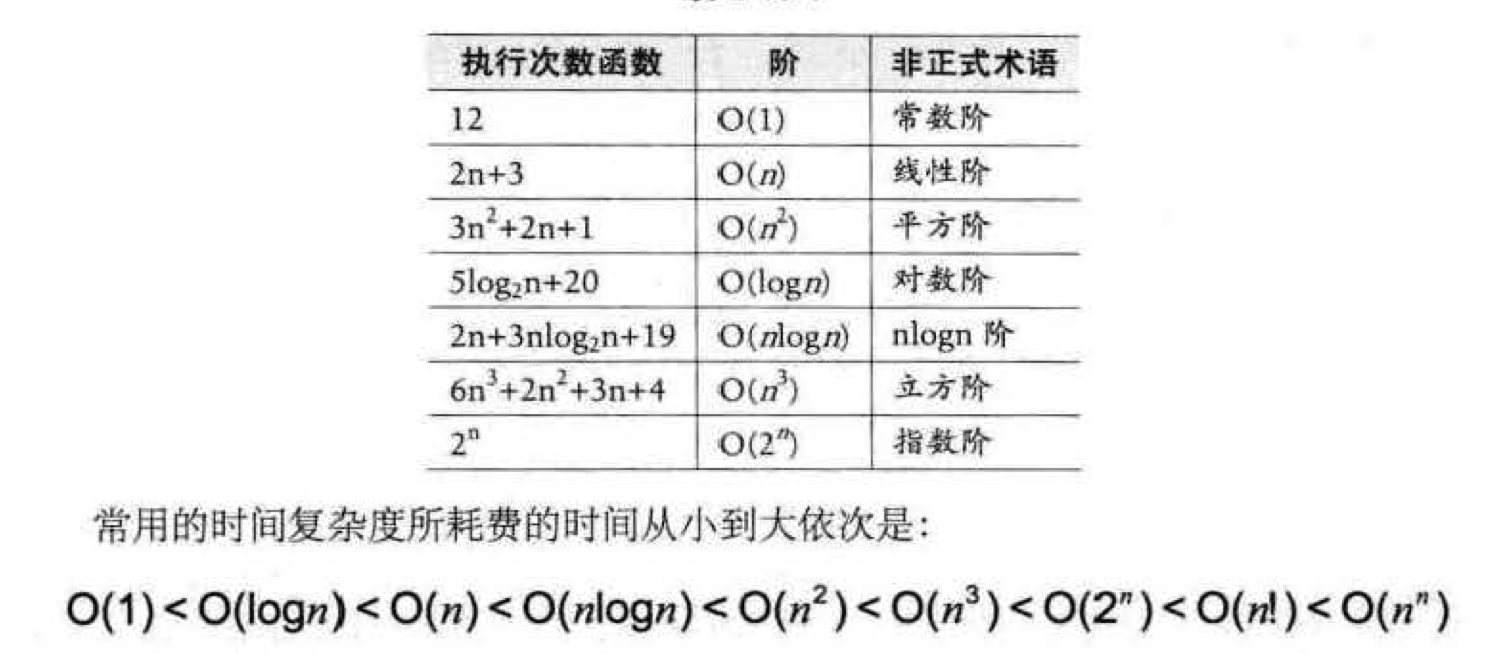
O(1) 叫常数阶, O(n) 线性阶(循环中有常数阶), O(n^2) 平方阶(嵌套循环).

对数阶

count = 1
whild count < n:
    count *= 2

O(logn)

算法的空间复杂度

算法的空间复杂度通过计算算法所需要的存储空间实现, 算法空间复杂的计算公式记作: S(n) = O(f(n)), 其中, n为问题的规模, f(n)为语句关于n所占存储空间的函数