字符串匹配算法
字符串匹配算法
KMP算法
KMP算法是由D.E.Knuth,J.H.Morris和V.R.Pratt提出的。
首先,要了解两个概念:
- 前缀 (prefix),指除了最后一个字符以外,一个字符串的全部头部组合;
- 后缀 (suffix),指除了第一个字符以外,一个字符串的全部尾部组合。
"部分匹配值" 就是"前缀"和"后缀"的最长的共有元素的长度。以"ABCDABD"为例,
- "A"的前缀和后缀都为空集,共有元素的长度为0;
- "AB"的前缀为[A],后缀为[B],共有元素的长度为0;
- "ABC"的前缀为[A, AB],后缀为[BC, C],共有元素的长度0;
- "ABCD"的前缀为[A, AB, ABC],后缀为[BCD, CD, D],共有元素的长度为0;
- "ABCDA"的前缀为[A, AB, ABC, ABCD],后缀为[BCDA, CDA, DA, A],共有元素为"A",长度为1;
- "ABCDAB"的前缀为[A, AB, ABC, ABCD, ABCDA],后缀为[BCDAB, CDAB, DAB, AB, B],共有元素为"AB",长度为2;
- "ABCDABD"的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB],后缀为[BCDABD, CDABD, DABD, ABD, BD, D],共有元素的长度为0。
假如我们要在字符串string="BBC ABCDAB ABCDABCDABDE" 中搜索 pattern="ABCDABD" 是否存在,通常我们从string的第一个位置开始比较,
如果不匹配就将pattern继续向右移动,移动位数 = 已匹配的字符数 - 对应的部分匹配值,直到找到匹配的子串或者返回无匹配。
例如,当pattern移动到如下位置时,发现前6个字符都匹配,只有最后一个字符D与空格不匹配,
这里前6个字符"ABCDAB"之中有两个"AB",那么它的"部分匹配值"就是2("AB"的长度)。

因此,下一步向右移动位数 = 6 - 2 = 4,

现在,只有前2个字符匹配("AB"),其"部分匹配值"为0,因此右移位数 = 2 - 0 = 2,
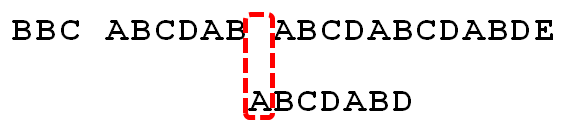
上图可见匹配长度为0,继续后移1位

现在的匹配字符是前6个,且其"部分匹配值"为2,继续后移4位

OK,此时完全匹配!如果还要继续搜索(即找出全部匹配),移动位数 = 7 - 0,再将搜索词向后移动7位,这里就不再重复了。
Boyer-Moore算法
1977年,德克萨斯大学的Robert S. Boyer教授和J Strother Moore教授发明了这种算法。
下面,我根据Moore教授自己的例子来解释这种算法。
1.


假定字符串为"HERE IS A SIMPLE EXAMPLE",搜索词为"EXAMPLE"。
2.


首先,"字符串"与"搜索词"头部对齐,从尾部开始比较。
这是一个很聪明的想法,因为如果尾部字符不匹配,那么只要一次比较,就可以知道前7个字符(整体上)肯定不是要找的结果。
我们看到,"S"与"E"不匹配。这时,"S"就被称为"坏字符"(bad character),即不匹配的字符。我们还发现,"S"不包含在搜索词"EXAMPLE"之中,这意味着可以把搜索词直接移到"S"的后一位。
3.


依然从尾部开始比较,发现"P"与"E"不匹配,所以"P"是"坏字符"。但是,"P"包含在搜索词"EXAMPLE"之中。所以,将搜索词后移两位,两个"P"对齐。
4.
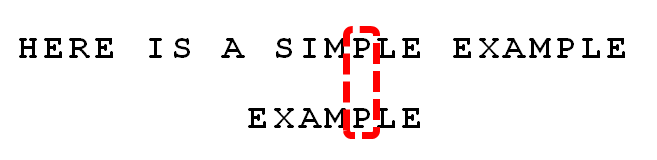

我们由此总结出"坏字符规则":
后移位数 = 坏字符的位置 - 搜索词中的上一次出现位置
如果"坏字符"不包含在搜索词之中,则上一次出现位置为 -1。
以"P"为例,它作为"坏字符",出现在搜索词的第6位(从0开始编号),在搜索词中的上一次出现位置为4,所以后移 6 - 4 = 2位。再以前面第二步的"S"为例,它出现在第6位,上一次出现位置是 -1(即未出现),则整个搜索词后移 6 - (-1) = 7位。
5.
依然从尾部开始比较,发现"MPLE"匹配,我们把这种情况称为"好后缀"(good suffix),即所有尾部匹配的字符串。注意,"MPLE"、"PLE"、"LE"、"E"都是好后缀。


根据"坏字符规则",这里坏字符为"I" (位置=2),此时搜索词应该后移 2 - (-1)= 3 位。问题是,此时有没有更好的移法?
我们知道,此时存在"好后缀"。所以,可以采用"好后缀规则":
后移位数 = 好后缀的位置 - 搜索词中的上一次出现位置
举例来说,如果字符串"ABCDAB"的后一个"AB"是"好后缀"。那么它的位置是5(从0开始计算,取最后的"B"的值),在"搜索词中的上一次出现位置"是1(第一个"B"的位置),所以后移 5 - 1 = 4位,前一个"AB"移到后一个"AB"的位置。
再举一个例子,如果字符串"ABCDEF"的"EF"是好后缀,则"EF"的位置是5 ,上一次出现的位置是 -1(即未出现),所以后移 5 - (-1) = 6位,即整个字符串移到"F"的后一位。
这个规则有三个注意点:
(1)"好后缀"的位置以最后一个字符为准。假定"ABCDEF"的"EF"是好后缀,则它的位置以"F"为准,即5(从0开始计算)。
(2)如果"好后缀"在搜索词中只出现一次,则它的上一次出现位置为 -1。比如,"EF"在"ABCDEF"之中只出现一次,则它的上一次出现位置为-1(即未出现)。
(3)如果"好后缀"有多个,则除了最长的那个"好后缀",其他"好后缀"的上一次出现位置必须在头部。比如,假定"BABCDAB"的"好后缀"是"DAB"、"AB"、"B",请问这时"好后缀"的上一次出现位置是什么?回答是,此时采用的好后缀是"B",它的上一次出现位置是头部,即第0位。这个规则也可以这样表达:如果最长的那个"好后缀"只出现一次,则可以把搜索词改写成如下形式进行位置计算"(DA)BABCDAB",即虚拟加入最前面的"DA"。
回到上文的这个例子。此时,所有的"好后缀"(MPLE、PLE、LE、E)之中,只有"E"在"EXAMPLE"还出现在头部,所以后移 6 - 0 = 6位。
6.

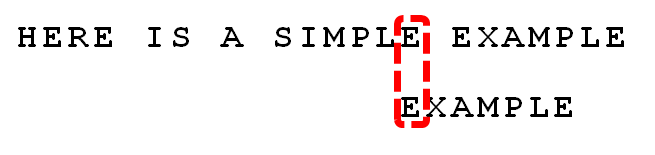
可以看到,"坏字符规则"只能移3位,"好后缀规则"可以移6位。所以,Boyer-Moore算法的基本思想是,每次后移这两个规则之中的较大值。
更巧妙的是,这两个规则的移动位数,只与搜索词有关,与原字符串无关。因此,可以预先计算生成《坏字符规则表》和《好后缀规则表》。使用时,只要查表比较一下就可以了。
7.


继续从尾部开始比较,"P"与"E"不匹配,因此"P"是"坏字符"。根据"坏字符规则",后移 6 - 4 = 2位。
8.


从尾部开始逐位比较,发现全部匹配,于是搜索结束。如果还要继续查找(即找出全部匹配),则根据"好后缀规则",后移 6 - 0 = 6位,即头部的"E"移到尾部的"E"的位置。
Rabin-Karp算法
Rabin-Karp算法,是由M.O.Rabin和R.A.Karp发明的一种基于散列的字符串查找算法。
通常情况下,基于散列的字符串查找步骤是:
- 首先计算模式字符串的散列函数;
- 然后利用相同的散列函数计算文本中所有可能的M个字符的子字符串的散列函数值并寻找匹配
但是这种方法比暴力查找还慢,因为计算散列值会涉及字符串中的每个字符。Rabin和Karp对上述方法进行了改进,发明了一种能够在常数时间内算出M个字符的子字符串散列值的方法。

递推文本串的散列值:
以Ti表示文本字符T[i],Xi表示文本串T[i...M-1-i]的整数值,其中M为模式串长度,则:
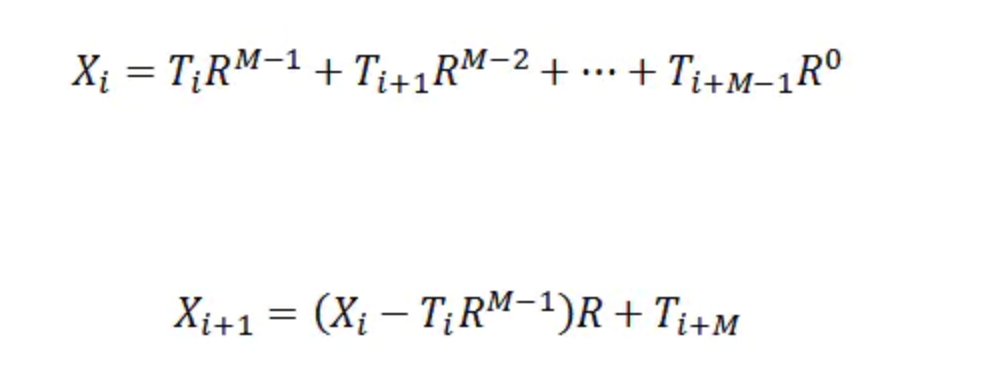
然后通过上述公式递推就可以得到字符串T[i+1...M-i]的hash值,即Xi+1 % P。
int charToInt(char a) { return a - 'a'; } int rkSearch(string t, string p) { size_t N = t.size(); size_t M = p.size(); if (M > N) return -1; const int R = 26; const long P = 2 << 30; // pow(2, 31);
long txtHash = 0, patternHash = 0; for (int n = 0; n < M; n++) { txtHash = (R * txtHash + charToInt(t[n])) % P; patternHash = (R * patternHash + charToInt(p[n])) % P; } if (txtHash == patternHash) { return 0; } // 计算R^M long RM = 1; for (int n = 1; n <= M; n++) { RM = (RM * R) % P; } for (int n = 1; n <= N - M; n++) { txtHash = (txtHash * R - charToInt(t[n - 1]) * RM + charToInt(t[n - 1 + M])) % P; if (txtHash == patternHash) return n; } return -1; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号