DS博客作业04——图
0.PTA得分截图

1.学习总结
图存储结构
邻接矩阵
#define MAXV //最大顶点个数
typedef struct
{
int no; //顶点编号
InfoType info; //顶点其他信息
} VertexType;
typedef struct //图的定义
{
int edges[MAXV][MAXV]; //邻接矩阵
int n,e; //顶点数,边数
VertexType vexs[MAXV]; //存放顶点信息
} MatGraph;
MatGraph g;//声明邻接矩阵存储的图
邻接表
typedef struct Vnode
{
Vertex data; //顶点信息
ArcNode *firstarc; //指向第一条边
} VNode;
typedef struct ANode
{
int adjvex; //该边的终点编号
struct ANode *nextarc; //指向下一条边的指针
InfoType info; //该边的权值等信息
} ArcNode;
typedef struct
{
VNode adjlist[MAXV] ; //邻接表
int n,e; //图中顶点数n和边数e
} AdjGraph;
AdjGraph *G;//声明一个邻接表存储的图G
图遍历
深度优先搜索(DFS)
1、从顶点出发
2、访问顶点,也就是根节点
3、依次从顶点的未被访问的邻接点出发,进行深度优先遍历;直至和顶点有路径相通的顶点都被访问
4、若此时尚有顶点未被访问,则从一个未被访问的顶点出发,重新进行深度优先遍历,直到所有顶点均被访问过为止
void DFS(ALGraph *G,int v)
{ ArcNode *p;
visited[v]=1; //置已访问标记
printf("%d ",v);
p=G->adjlist[v].firstarc;
while (p!=NULL)
{
if (visited[p->adjvex]==0) DFS(G,p->adjvex);
p=p->nextarc;
}
}
时间复杂度
邻接表:O(n+e)
邻接矩阵:O(n^2)
广度优先遍历(BFS)
1、访问初始点v,接着访问v的所有未被访问过的邻接点
2、按照次序访问每一个顶点的所有未被访问过的邻接点
3、依此类推,直到图中所有顶点都被访问过
遍历非连通图
void BFS1(AdjGraph *G)
{ int i;
for (i=0;i<G->n;i++) //遍历所有未访问过的顶点
if (visited[i]==0)
BFS(G,i);
}
时间复杂度:O(n+e)
图应用
判断图是否连通
DFS遍历
int visited[MAXV];
bool Connect(AdjGraph *G) //判断无向图G的连通性
{ int i;
bool flag=true;
for (i=0;i<G->n;i++) //visited数组置初值
visited[i]=0;
DFS(G,0); //调用前面的中DSF算法,从顶点0开始深度优先遍历
for (i=0;i<G->n;i++)
if (visited[i]==0)
{ flag=false;
break;
}
return flag;
}
BFS()
{ int count = 0 ;
boolean flag = false;
Queue Q = new Queue();
visited = new int[this.vertexNum];
while(!Q.isEmpty())
{
int s = Q.front();
Q.remove();
visited[s] = 1;
count ++;
for(int j=0; j<this.vertexNum; j++)
{
if(this.a[s][j] == 1 && visited[j] == 0 )
{
visited[j] = 1;
Q.add(j);
}
}
}
if(count == this.vertexNum)
flag = true;
return flag;
}
最短路径
在带权有向图中A点(源点)到达B点(终点)的多条路径中,寻找一条各边权值之和最小的路径,即最短路径
一个顶点到其余各顶点的最短路径——Dijkstra算法
引进两个集合S和U。
S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度)
U则是记录还未求出最短路径的顶点(以及该顶点到起点s的距离)
过程
1、S只包含起点s;U包含除s外的其他顶点,且U中顶点的距离为”起点s到该顶点的距离”[U中顶点v的距离为(s,v)的长度,如果s和v不相邻,则v的距离为∞]
2、从U中选出”距离最短的顶点k”,并将顶点k加入到S中;同时从U中移除顶点k
3、更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离,是因为上一步中确定了k是求出最短路径的顶点,从而可以利用k来更新其它顶点的距离;
例如,(s,v)的距离可能大于(s,k)+(k,v)的距离
4、重复2和3,直到遍历完所有顶点。
void Dijkstra(MatGraph g,int v)
{
int dist[MAXV],path[MAXV];
int s[MAXV];
int mindis,i,j,u;
for (i=0;i<g.n;i++)
{
dist[i]=g.edges[v][i]; //距离初始化
s[i]=0; //s[]置空
if (g.edges[v][i]<INF) //路径初始化
path[i]=v; //顶点v到i有边时
else
path[i]=-1; //顶点v到i没边时
}
s[v]=1;
for (i=0;i<g.n;i++) //循环n-1次
{
mindis=INF;
for (j=0;j<g.n;j++)
if (s[j]==0 && dist[j]<mindis)
{
u=j;
mindis=dist[j];
}
s[u]=1; //顶点u加入S中
for (j=0;j<g.n;j++) //修改不在s中的顶点的距离
if (s[j]==0)
if (g.edges[u][j]<INF &&dist[u]+g.edges[u][j]<dist[j])
{
dist[j]=dist[u]+g.edges[u][j];
path[j]=u;
}
}
Dispath(dist,path,s,g.n,v); //输出最短路径
}
时间复杂度O(n^2)
不适用带负权值的带权图求单源最短路径
不适用求最长路径长度
每一对顶点之间的最短路径——Floyd算法
创建一个二维数组Path路径数组,用于存放任意一对顶点之间的最短路径。每个单元格的内容表示从i点到j点途经的顶点
void Floyd(MatGraph g) //求每对顶点之间的最短路径
{ int A[MAXVEX][MAXVEX]; //建立A数组
int path[MAXVEX][MAXVEX]; //建立path数组
int i, j, k;
for (i=0;i<g.n;i++)
for (j=0;j<g.n;j++)
{ A[i][j]=g.edges[i][j];
if (i!=j && g.edges[i][j]<INF)
path[i][j]=i; //i和j顶点之间有一条边时
else //i和j顶点之间没有一条边时
path[i][j]=-1;
}
for (k=0;k<g.n;k++) //求Ak[i][j]
{
for (i=0;i<g.n;i++)
for (j=0;j<g.n;j++)
if (A[i][j]>A[i][k]+A[k][j]) //找到更短路径
{
A[i][j]=A[i][k]+A[k][j]; //修改
path[i][j]=k; //修改经过顶点k
}
}
}
时间复杂度为O(n^3)
空间复杂度为O(n^2)
最小生成树
生成树:一个连通图的生成树是指一个连通子图,它含有图中全部n个顶点,但只有足以构成一棵树的n-1条边。
一颗有n个顶点的生成树有且仅有n-1条边,如果生成树中再添加一条边,则必定成环。
最小生成树:在连通网的所有生成树中,所有边的代价和最小的生成树,称为最小生成树。
Prim算法
“加点法”,每次选择权值最小的边对应的点,加入到最小生成树中。
#define INF 32767 //INF表示∞
void Prim(MGraph g,int v)
{ int lowcost[MAXV],min,closest[MAXV],i,j,k;
for (i=0;i<g.n;i++) //给lowcost[]和closest[]置初值
{ lowcost[i]=g.edges[v][i];closest[i]=v;}
for (i=1;i<g.n;i++) //找出(n-1)个顶点
{ min=INF;
for (j=0;j<g.n;j++) // 在(V-U)中找出离U最近的顶点k
if (lowcost[j]!=0 && lowcost[j]<min)
{
min=lowcost[j]; k=j; /k记录最近顶点的编号}
printf(" 边(%d,%d)权为:%d\n",closest[k],k,min);
lowcost[k]=0; //标记k已经加入U
for (j=0;j<g.n;j++) //修改数组lowcost和closest
if (lowcost[j]!=0 && g.edges[k][j]<lowcost[j])
{
lowcost[j]=g.edges[k][j];
closest[j]=k;
}
}
}
Kruskal算法
“加边法”,初始最小生成树边数为0,每次选择一条满足条件的最小权值边,加入到最小生成树的边集合里。
void Kruskal(AdjGraph *g)
{ int i,j,u1,v1,sn1,sn2,k;
int vset[MAXV]; //集合辅助数组
Edge E[MaxSize]; //存放所有边
k=0; //E数组的下标从0开始计
for (i=0;i<g.n;i++) //由g产生的边集E,邻接表
{
p=g->adjlist[i].firstarc;
while(p!=NULL)
{
E[k].u=i;E[k].v=p->adjvex;
E[k].w=p->weight;
k++; p=p->nextarc;
}
}
Sort(E,g.e); //用快排对E数组按权值递增排序
for (i=0;i<g.n;i++) //初始化集合
vset[i]=i;
k=1; //k表示当前构造生成树的第几条边,初值为1
j=0; //E中边的下标,初值为0
while (k<g.n) //生成的顶点数小于n时循环
{
u1=E[j].u;v1=E[j].v; //取一条边的头尾顶点
sn1=vset[u1];
sn2=vset[v1]; //分别得到两个顶点所属的集合编号
if (sn1!=sn2) //两顶点属于不同的集合
{
printf(" (%d,%d):%d\n",u1,v1,E[j].w);
k++; //生成边数增1
for (i=0;i<g.n;i++) //两个集合统一编号
if (vset[i]==sn2) //集合编号为sn2的改为sn1
vset[i]=sn1;
}
j++; //扫描下一条边
}
}
拓扑排序
1、从DGA图中找到一个没有前驱的顶点输出
2、删除以这个点为起点的边。(它的指向的边删除,为了找到下个没有前驱的顶点)
3、重复上述,直到最后一个顶点被输出。如果还有顶点未被输出,则说明有环
void TopSort(AdjGraph *G) //拓扑排序算法
{
int i,j;
int St[MAXV],top=-1; //栈St的指针为top
ArcNode *p;
for (i=0;i<G->n;i++) //入度置初值0
G->adjlist[i].count=0;
for (i=0;i<G->n;i++) //求所有顶点的入度
{
p=G->adjlist[i].firstarc;
while (p!=NULL)
{
G->adjlist[p->adjvex].count++;
p=p->nextarc;
}
}
for (i=0;i<G->n;i++) //将入度为0的顶点进栈
if (G->adjlist[i].count==0)
{
top++;
St[top]=i;
}
while (top>-1) //栈不空循环
{
i=St[top];top--; //出栈一个顶点i
printf("%d ",i); //输出该顶点
p=G->adjlist[i].firstarc; //找第一个邻接点
while (p!=NULL) //将顶点i的出边邻接点的入度减1
{
j=p->adjvex;
G->adjlist[j].count--;
if (G->adjlist[j].count==0) //将入度为0的邻接点进栈
{
top++;
St[top]=j;
}
p=p->nextarc; //找下一个邻接点
}
}
}
关键路径
AOE网:在一个表示工程的带权有向图中,用顶点表示事件(如V0),用有向边表示活动(如<v0,v1> = a1),边上的权值表示活动的持续时间,
称这样的有向图为边表示的活动的网,简称AOE网(activity on edge network)
源点:在AOE网中,没有入边的顶点称为源点;如顶点V0
终点:在AOE网中,没有出边的顶点称为终点;如顶点V3
AOE网的性质:
1、只有在进入某顶点的活动都已经结束,该顶点所代表的事件才发生
2、只有在某顶点所代表的事件发生后,从该顶点出发的各活动才开始
在AOE网中,所有活动都完成才能到达终点,因此完成整个工程所必须花费的时间(即最短工期)应该为源点到终点的最大路径长度
具有最大路径长度的路径称为关键路径
关键路径上的活动称为关键活动
对图的认识及学习体会
图对我而言非常的难,我对于其中的知识大部分都不太理解,导致了学习进度慢。
图这种结构已经非常接近现实了,多对多的关系令它能够做更多的事。
2.阅读代码
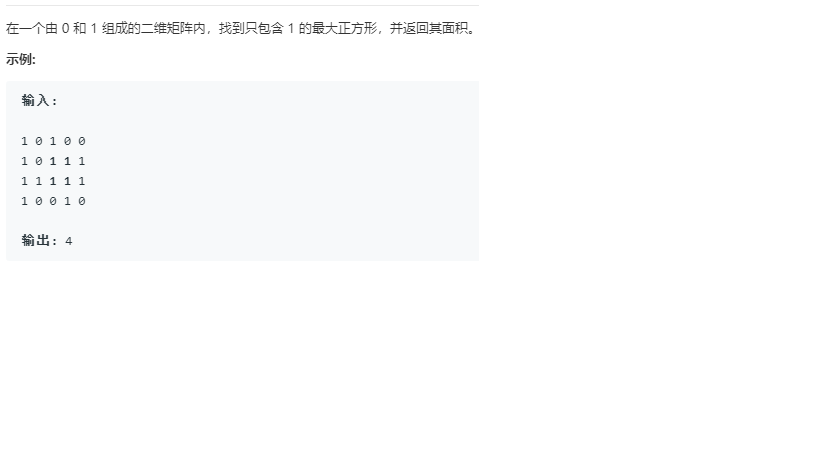
2.1 最大正方形
int maximalSquare(vector<vector<char>>& matrix)
{
if (matrix.size() == 0 || matrix[0].size() == 0)
{
return 0;
}
int maxSide = 0;
int rows = matrix.size(), columns = matrix[0].size();
for (int i = 0; i < rows; i++)
{
for (int j = 0; j < columns; j++)
{
if (matrix[i][j] == '1')
{
// 遇到一个 1 作为正方形的左上角
maxSide = max(maxSide, 1);
// 计算可能的最大正方形边长
int currentMaxSide = min(rows - i, columns - j);
for (int k = 1; k < currentMaxSide; k++)
{
// 判断新增的一行一列是否均为 1
bool flag = true;
if (matrix[i + k][j + k] == '0') break;
for (int m = 0; m < k; m++)
{
if (matrix[i + k][j + m] == '0' || matrix[i + m][j + k] == '0')
{
flag = false;
break;
}
}
if (flag) maxSide = max(maxSide, k + 1);
else break;
}
}
}
}
int maxSquare = maxSide * maxSide;
return maxSquare;
}
2.1.1 设计思路
由于正方形的面积等于边长的平方,因此要找到最大正方形的面积,首先需要找到最大正方形的边长,然后计算最大边长的平方即可。
1、遍历矩阵中的每个元素,每次遇到1,则将该元素作为正方形的左上角;
2、确定正方形的左上角后,根据左上角所在的行和列计算可能的最大正方形的边长(正方形的范围不能超出矩阵的行数和列数),在该边长范围内寻找只包含 1 的最大正方形;
3、每次在下方新增一行以及在右方新增一列,判断新增的行和列是否满足所有元素都是1。
时间复杂度:O(mn*min(m,n)^2),其中 m 和 n 是矩阵的行数和列数。
空间复杂度:O(1)
2.1.2 伪代码
int maximalSquare(vector<vector<char>>& matrix)
{
if (空矩阵)
return 0;
定义整型变量maxside记录最长边的大小
记录矩阵行列大小
for (int i = 0; i < rows; i++)
{
for (int j = 0; j < columns; j++)
{
if (遇到一个 1 作为正方形的左上角)
{
计算可能的最大正方形边长
int currentMaxSide = min(rows - i, columns - j);
for (int k = 1; k < currentMaxSide; k++)
{
判断新增的一行一列是否均为 1
}
}
}
}
int maxSquare = maxSide * maxSide;
return maxSquare;
}
2.1.3 运行结果
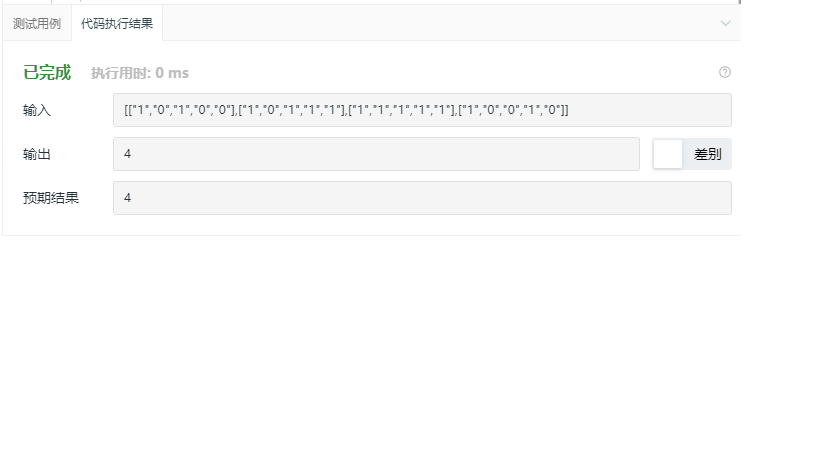
2.1.4 解题优势及难点
此题使用暴力法,难点在于如何降低时间复杂度。
解题优势在于对面积较小的正方形的遍历不会重复遍历邻接矩阵
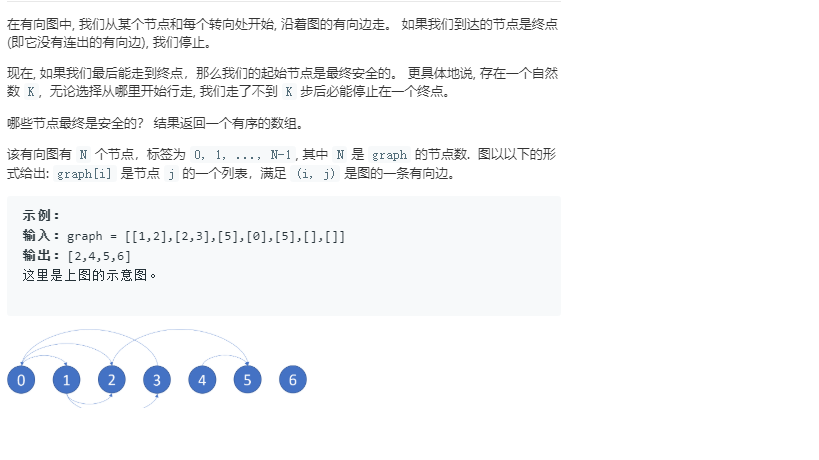
2.2 找到最终的安全状态
class Solution {
public:
vector<int> eventualSafeNodes(vector<vector<int>>& graph) {
int n = graph.size();
vector<int> outDegree(n, 0); // 维护出度
vector<vector<int>> revGraph(n, vector<int>{});
vector<int> ans;
for (int i =0; i < n; i++){
outDegree[i] = graph[i].size();
for (auto &end : graph[i]){
revGraph[end].push_back(i);
}
}
queue<int> q;
for (int i =0; i< n ; i++){
if (outDegree[i] == 0) q.push(i);
}
while (!q.empty()){
int f = q.front();
ans.push_back(f);
q.pop();
for (auto start: revGraph[f]){
outDegree[start]--;
if (outDegree[start] == 0) q.push(start);
}
}
sort(ans.begin(), ans.end());
return ans;
}
};
2.2.1 设计思路
定义安全的点:路径终点,也就是出度为0的点
定义最终安全的点:从起始节点开始,可以沿某个路径到达终点,那么起始节点就是最终安全的点。
1、找到出度为0的顶点,这些点是安全的点
2、逆向删除以出度为0的顶点为弧头的边,弧尾的出度减一
3、重复上面两步,直到不存在出度为0的顶点
时间复杂度:O(n^2)
空间复杂度:O(n^2)
2.2.2 伪代码
遍历顶点
if(顶点v出度度为0)
v入队列
while(队列非空)
{
top出队
遍历逆向邻接表
{
top所有的邻接点出度减一
if (邻接点出度为0)
邻接点入队
}
}
2.2.3 运行结果
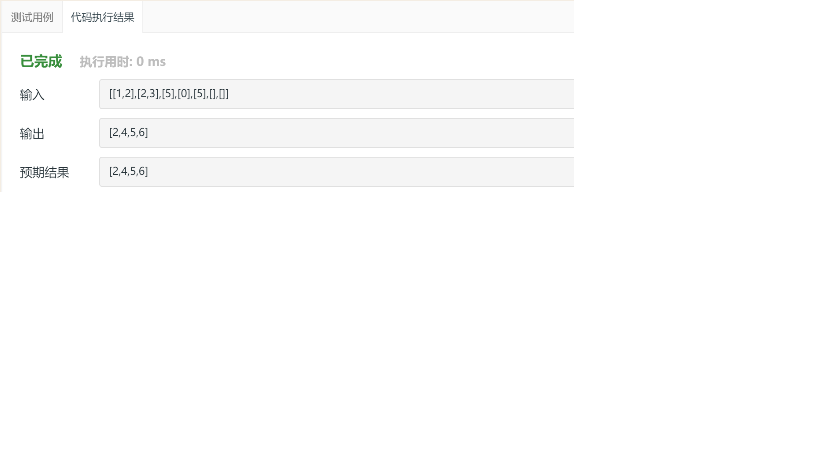
2.2.4 解题优势及难点
优势:使用拓扑排序,而不是BFS或DFS
难点:逆向边的操作
2.3 不邻接植花

class Solution {
public:
//static const int MAXV=10000;
//int G[MAXV][MAXV]={0};
vector<int> gardenNoAdj(int N, vector<vector<int>>& paths) {
vector<int> G[N];
for (int i=0; i<paths.size(); i++){//建立邻接表
G[paths[i][0]-1].push_back(paths[i][1]-1);
G[paths[i][1]-1].push_back(paths[i][0]-1);
}
vector<int> answer(N,0);//初始化全部未染色
for(int i=0; i<N; i++){
set<int> color{1,2,3,4};
for (int j=0; j<G[i].size(); j++){
color.erase(answer[G[i][j]]);//把已染过色的去除
}
answer[i]=*(color.begin());//染色
}
return answer;
}
};
2.3.1 设计思路
1、根据paths建立邻接表;
2、默认所有的花园先不染色,即染0;
3、从第一个花园开始走,把与它邻接的花园的颜色从color{1,2,3,4}这个颜色集中删除;
4、删完了所有与它相邻的颜色,就可以把集合中剩下的颜色随机选一个给它了,为了简单,将集合中的第一个颜色赋给当前花园;
5、循环3和4到最后一个花园。
2.3.2 伪代码
建立邻接表
初始化全部花园未种花answer(N,0);
for i=0 to N-1 do
每次循环都要初始化color
for j=0 to G[i].size()-1 do
把已染过色的去除
end for
对当前顶点种花answer[i]=*(color.begin());
end for
return answer;
}
};
2.3.3 运行结果
2.3.4 解题优势及难点
优势:使用邻接表存储数据
难点:color的应用及操作


 浙公网安备 33010602011771号
浙公网安备 33010602011771号