DS博客作业03--树
0.PTA得分截图
1.本周学习总结
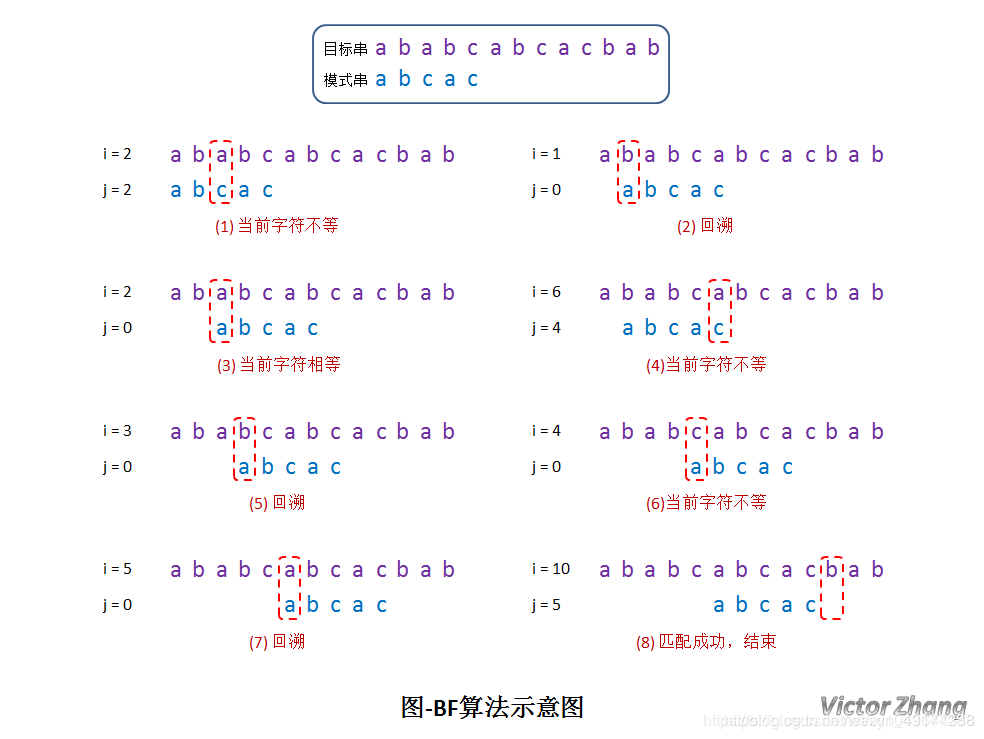
BF算法
从目标串T的的第一个字符起与模式串P的第一个字符比较。
若相等,则继续对字符进行后续的比较;否则目标串从第二个字符起与模式串的第一个字符重新比较。
直至模式串中的每个字符依次和目标串中的一个连续的字符序列相等为止,此时称为匹配成功,否则匹配失败。
时间复杂度为O(mn)。
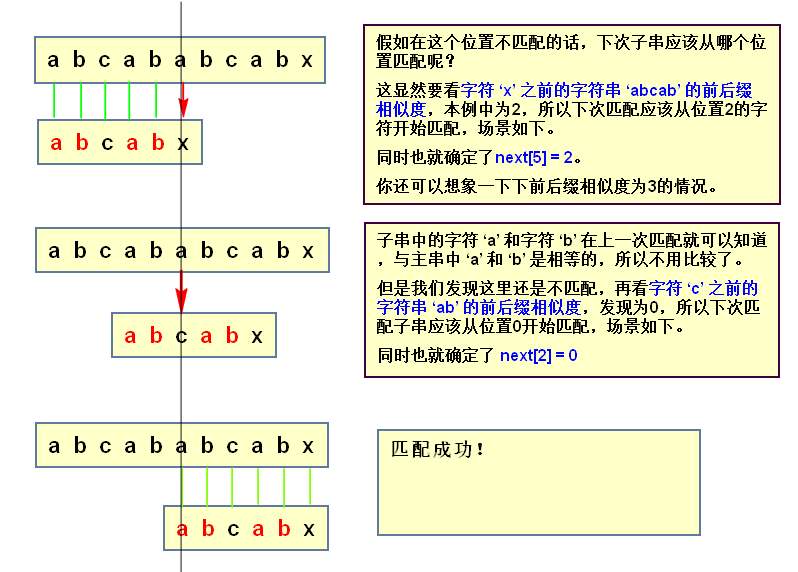
KMP算法
算法的核心是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。
对于模式串t的每个元素 t[j],都存在一个实数k,使得模式串t开头的k个字符
(t[0] t[1] … t[k-1])依次与 t[j] 前面的k(t[j-k] t[j-k+1] … t[j-1],这里第一个字符 t[j-k]最多从t[1]开始,所以k < j)
个字符相同。如果这样的k有多个,则取最大的一个。
具体实现是通过一个next()函数实现,函数本身包含了模式串的局部匹配信息,next[j]=MAX{k}。
时间复杂度O(m+n)。
二叉树
顺序存储结构
对每个结点编号,以各结点的编号为下标,把各结点的值对应存储到一维数组中。
每个结点的编号与等深度的满二叉树中对应结点的编号相等,即树根结点的编号为1,接着按照从上到下和从左到右的次序,
若一个结点的编号为i,则左、右孩子的编号分别为2i和2i+1。

顺序存储结构对于存储完全二叉树是合适的,它能够充分利用存储空间,
但对于一般二叉树,特别是对于那些单支结点较多的二叉树来说是很不合适的,因为可能只有少数存储位置被利用,而大多数的存储位置空着。
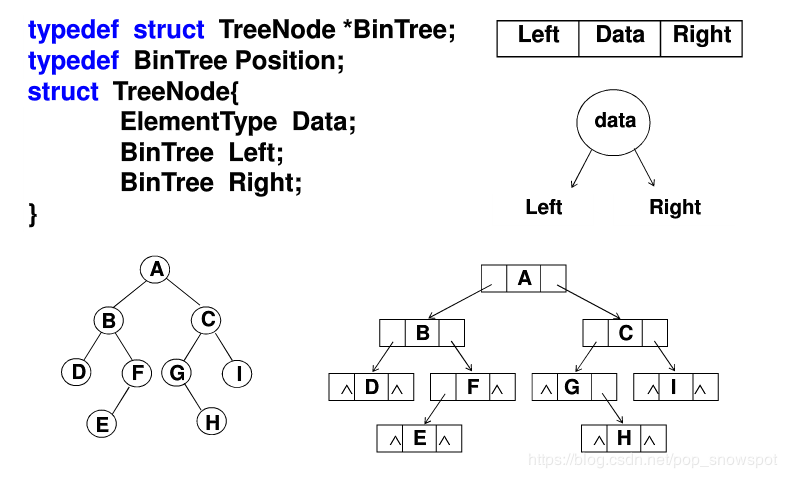
链式存储结构
每个结点中设置3个域:值域、左指针域和右指针域。
链式存储结构(带双亲)
在上面的结点结构中再增加一个parent指针域,用来指向其双亲结点。
这种存储结构既便于查找孩子结点,也便于查找双亲结点,同时带来存储空间的相应增加。

先序遍历递归建树
BTree CreatTree(string str, int &i)
{
BTree bt;
if (i > len - 1) return NULL;
if (str[i] == '#') return NULL;
bt = new BTNode;
bt->data = str[i];
bt->lchild = CreatTree(str, ++i);
bt->rchild = CreatTree(str, ++i);
return bt;
}
根据中序序列和后序序列建树
BTree CreateBTree(char inOd[], char postOd[], int n)
{
if (n == 0)
return NULL;
BTree btRoot = new BTNode;
btRoot->data = postOd[n-1]; //后序序列最后一个元素一定是根节点
char lInOd[N], rInOd[N];
char lPostOd[N], rPostOd[N];
int n1, n2;
n1 = n2 = 0;
//根据根节点将中序序列分为左子树和右子树
for (int i = 0; i < n; i++)
{
if (i <= n1 && inOd[i] != btRoot->data)
lInOd[n1++] = inOd[i];
else if (inOd[i] != postOd[n-1])
rInOd[n2++] = inOd[i];
}
//根据一个树的后序序列的长度等于中序序列且后序遍历是先左子树再右子树
//将后序序列分为左子树和右子树
int m1, m2;
m1 = m2 = 0;
for (int i = 0; i < n-1; i++)
{
if (i < n1)
lPostOd[m1++] = postOd[i];
else
rPostOd[m2++] = postOd[i];
}
btRoot->lChild = CreateBTree(lInOd, lPostOd, n1);
btRoot->rChild = CreateBTree(rInOd, rPostOd, n2);
return btRoot;
}
前序遍历
void PreOrder(BTreeNode* BT) {
if(BT != NULL) {
cout << BT->data << ' '; //访问根结点
PreOrder(BT->left); //前序遍历左子树
PreOrder(BT->right); //前序遍历右子树
}
}
中序遍历
void InOrder(BTreeNode* BT) {
if(BT != NULL) {
InOrder(BT->left); //中序遍历左子树
cout << BT->data << ' '; //访问根结点
InOrder(BT->right); //中序遍历右子树
}
}
后序遍历
void PostOrder(BTreeNode* BT) {
if(BT != NULL) {
PostOrder(BT->left); //后序遍历左子树
PostOrder(BT->right); //后序遍历右子树
cout << BT->data << ' '; //访问根结点
}
}
层次遍历
void AllPath2(BTree b)
{
int k;
BTree p;
QuType *qu; //定义非非环形队列指针
InitQueue(qu); //初始化队列
b->parent=-1; //创建根结点对应的队列元素
enQueue(qu,b); //根结点进队
while (!QueueEmpty(qu)) //队不空循环
{
deQueue(qu,p); //出队
if (p->lchild==NULL && p->rchild==NULL)
{
k=qu->front; //输出结点p到根结点的路径逆序列
while (qu->data[k]->parent!=-1)
{
printf("%c->",qu->data[k]->data);
k=qu->data[k]->parent;
}
printf("%c\n",qu->data[k]->data);
}
}
}
树
双亲存储结构
typedef struct
{ ElemType data; //结点的值
int parent; //指向双亲的位置
} PTree[MaxSize];
不利于寻找孩子结点
孩子链存储结构
typedef struct node
{ ElemType data; //结点的值
struct node *sons[MaxSons]; //指向孩子结点
} TSonNode;
十分容易造成空间浪费
不便于寻找双亲结点
孩子兄弟链存储结构
typedef struct tnode
{ ElemType data; //结点的值
struct tnode *son; //指向兄弟
struct tnode *brother; //指向孩子结点
} TSBNode;
线索二叉树
对于各种二叉链表,不管二叉树的形态如何,空链域的个数总是多过非空链域的个数。
n个结点的二叉链表共有2n个链域,非空链域为n-1个,但其中的空链域却有n+1个。

利用原来的空链域存放指针,指向树中其他结点。这种指针称为线索。
线索化的实质就是将二叉链表中的空指针改为指向前驱或后继的线索。
由于前驱和后继信息只有在遍历该二叉树时才能得到,所以,线索化的过程就是在遍历的过程中修改空指针的过程。
哈夫曼树
又称最优树,是一类带权路径长度最短的树。
树的路径长度:从树根到每一结点的路径之和。
权:赋予某个实体的一个量,是对实体的某个或某些属性的数值描述。在数据结构中,实体有结点(元素)和边(关系)两大类,所以对应有结点权和边权。
结点的带权路径长度:从该结点到树根之间的路径长度与结点上权的乘积。
树的带权路径长度:树中所有叶子结点的带权路径长只和。
哈夫曼树:假设有m个权值{w1,w2,w3,...,wn},可以构造一棵含有n个叶子结点的二叉树,每个叶子结点的权为wi,则其中带权路径长度WPL最小的二叉树称做最优二叉树或哈夫曼树。
哈夫曼树并不唯一,但带权路径长度一定是相同的。
构造哈夫曼树
1、根据给定的n个权值{w1, w2, w3 ... wn },构造n棵只有根节点的二叉树,令起权值为wj
2、在森林中选取两棵根节点权值最小的树作为左右子树,构造一颗新的二叉树,置新二叉树根节点权值为其左右子树根节点权值之和。左子树的权值应小于右子树的权值
3、从森林中删除这两棵树,同时将新得到的二叉树加入森林中(换句话说,之前的2棵最小的根节点已经被合并成一个新的结点了)
4、重复上述两步,直到只含一棵树为止,即哈夫曼树

并查集
初始化
把每个数据所在集合初始化为其自身。
查找
查找元素所在的集合,即根节点。
根节点父亲为本身
合并
将两个元素所在的集合合并为一个集合。
合并之前,应先判断两个元素所在树的高度。
1.2 对树的认识及学习体会
树是一种非线性结构,对于信息的存储更加贴近实际,能够解决的问题也更多。
对于树而言,我觉得最难的是如何建树,因为树有着多种多样的存储结构,如双亲存储,孩子链存储,孩子兄弟链存储。
树的应用中大量使用了递归,因而代码精简,但是较为难懂,需要认真的钻研。
2.阅读代码
2.1 二叉树最大宽度
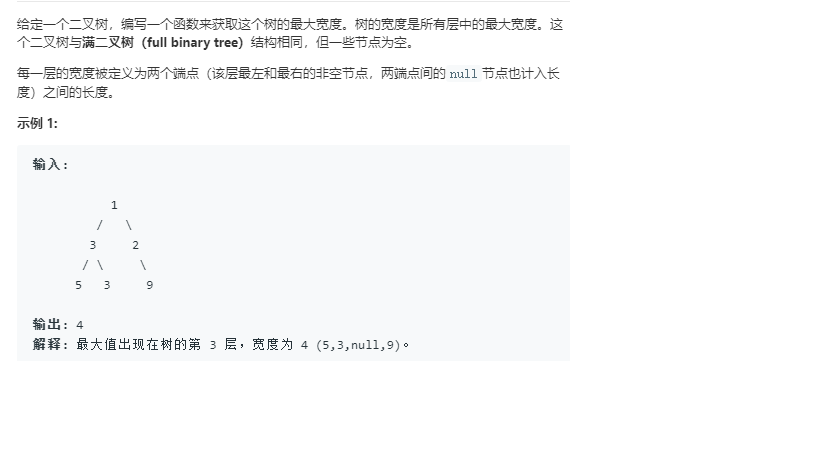
int widthOfBinaryTree(TreeNode* root)
{
int ans = 0;
deque<TreeNode*> dque;
TreeNode* tmp = NULL;
if(root == NULL) return ans;
dque.push_back(root);
while(!dque.empty())
{
// 出队前需要判断队列是否为空.
while(!dque.empty()&&dque.front() == NULL) dque.pop_front();
while(!dque.empty()&&dque.back() == NULL) dque.pop_back();
int n = dque.size();
if(n == 0) break;
ans = max(ans, n);
for(int i = 0; i < n; ++i){
tmp = dque.front();dque.pop_front();
dque.push_back(tmp == NULL ? NULL:tmp->left);
dque.push_back(tmp == NULL ? NULL:tmp->right);
}
}
return ans;
}
2.1.1 设计思路
采用双端队列,二叉树的层次遍历。每层遍历前,在队列中清除左右两边的null指针。
null指针的左右两个儿子均为null。
时间复杂度O(n)
空间复杂度O(n)
2.1.2 伪代码
int widthOfBinaryTree(TreeNode* root)
{
整型变量ans记录层宽度,初始化为0
定义双端队列dque
定义一个空指针tmp
if(空树)
return ans;
根节点入队
while(队列不空)
{
while(队列不空且dque的队头为NULL) 队头出队;
while(队列不空且dque的队尾为NULL) 队尾出队;
整型变量n获取队列大小
if(n == 0) break;//队列为空
将n和ans的最大值赋给ans
for(int i = 0; i < n; ++i)
{
队头赋值给tmp
队头出队
tmp的左右结点进队
}
}
return ans;
}
2.1.3 运行结果

2.1.4 该题目解题优势及难点
优势:运用了关于双端队列,对队列的头尾都可以进行插入删除操作。
难点:结点为空时依旧占有一个宽度,计算队列最左边非空位置开始到最右边非空位置的距离。
2.2 二叉树的堂兄弟节点
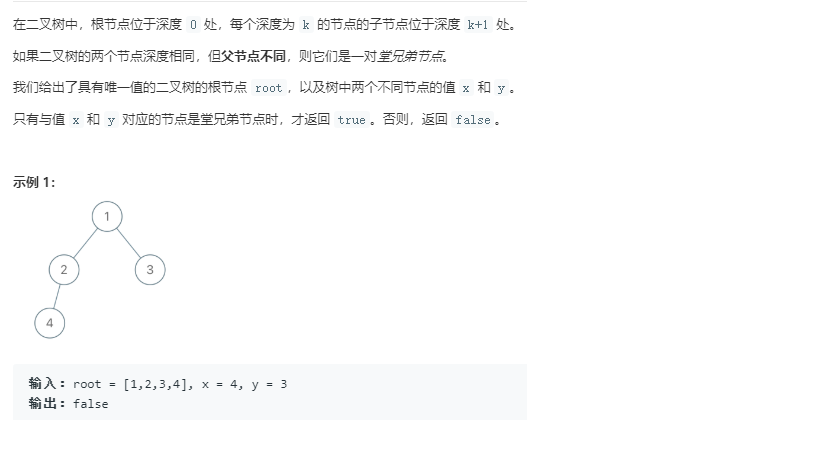
void dfs(TreeNode* root, TreeNode* p, int d, int x, int& depth, TreeNode** parent)
{
if (root == NULL) return;
if (root->val == x)
{
*parent = p;
depth = d;
return;
}
dfs(root->left, root, d + 1, x, depth, parent);
dfs(root->right, root, d + 1, x, depth, parent);
}
bool isCousins(TreeNode* root, int x, int y)
{
int dx = 0;
int dy = 0;
TreeNode* px = NULL;
TreeNode* py = NULL;
dfs(root, NULL, 0, x, dx, &px);
dfs(root, NULL, 0, y, dy, &py);
return (dx == dy) && (px != py);
}
2.2.1 设计思路
先找到x和y的深度和父节点,然后比较深度和父节点是否相同来判断是否是堂兄弟节点
时间复杂度O(n)
空间复杂度O(1)
2.2.2 伪代码
void dfs(TreeNode* root, TreeNode* p, int d, int x, int& depth, TreeNode** parent)
{
获得深度及父节点;
}
bool isCousins(TreeNode* root, int x, int y)
{
定义dx,dy记录深度
定义px,py来记录父节点
找x;
找y;
深度相同,父节点不相同,则是二叉树的堂兄弟节点
}
2.2.3 运行结果


 浙公网安备 33010602011771号
浙公网安备 33010602011771号