2024解题报告

2024.01.02

1.圣诞决斗

算法：博弈论

2.赛道修建

算法：带权并查集+动态规划dp

3.哀

算法：根号分治

已知一个数列，支持两种操作：

• 将所有 \(i~mod~k \in [l,r]\) 的 \(a_i\) 加上 \(x\)。

• 查询 \(\sum\limits_{i=l}^{r}a_i\)

很经典的根号分治，对于修改操作对于 \(k\) 进行根号分治：

• \(k > \sqrt{n}\) 直接分块暴力加。

• \(k \le \sqrt{n}\) 把每 \(k\) 个看作一个周期，处理周期前缀即可。

时间复杂度 \(O(n \sqrt n)\)。

2024.01.04

1.缆车

算法：分块+凸包

有 \(n\) 个点，每个点有坐标 \(P(i)\)，求对于每个点 \(i\) 求第一个在射线 \(P(i)P(i+1)\) 上方的点 \(P(j)(j > i)\)。

我们考虑对于两个点形成的一条线段，如果线段的斜率大于射线的斜率，相当于随着 \(x\) 的增加线段在逐渐向射线上方移动，所以我们对于每个块维护一个斜率单调递减的上凸包，二分最后一次斜率大于射线斜率的位置，即为最有可能在射线上方的位置，时间复杂度 \(O(n \sqrt{n~log~n})\)。

2.鸥

算法：斯特林数

3.卡牌

算法：线段树+树状数组

2024.01.08

1.回归

算法：递推

2.或

算法：并查集

给出 \(n\) 个数，求将数分为两个非空集合且按位或相等的方案数。

合法情况并不好计算，所以考虑容斥，不合法情况即为在一个二进制位上所以为 \(1\) 的数都同时在一个集合内。于是我们每次可以钦定哪些位上的 \(1\) 都在一个集合中，对于一个数在 \(i\) 和 \(j\) 位同时为 \(1\) 时，将这两位进行并查集，每次钦定的答案即为： \(2^{cnt}-2\)（\(cnt\) 为并查集数量，减去全集和空集），容斥系数 \(-1\)。

但我们又遇到一个问题，如何计算在钦定集合的反集的子集中的数，我们采用高维前缀和计算即可。

3.测测你的字符串哈希

算法：AC自动机

2024.01.10

1.塑料内存条

算法：根号分治

给出 \(n\) 个不可重集，要求以下三种操作：

• 在集合 \(x\) 中添加元素 \(y\)

• 将 \(y\) 集合中的所有元素加入 \(x\) 集合中，且后续操作不出现 \(y\) 集合。

• 求集合 \(x\) 和集合 \(y\) 的交集的编号之和。

一道小清新根号分治，发现一二操作用 \(set\) 加启发式合并能做到 \(O(n~log^2~n)\) ，而三操作只能做到 \(O(min(siz_x,siz_y))\)，所以我们考虑根号分治：

• 对于 \(siz_x \le \sqrt{n}\)，\(set\) 集合维护暴力查询即可。

• 对于 \(siz_x > \sqrt{n}\)，我们需要对于每次加元素暴力维护和其他最多 \(\sqrt{n}\) 个大集合之间的答案。

2.冒泡π序

算法：勾股数+莫比乌斯反演

3.测测你的高斯消元

算法：行列式+树形dp

2024.01.14

1.早八

算法：线段树

2.派对

算法：动态规划dp+矩阵加速

3.间谍

算法：凸包

2024.01.15

1.签到题

算法：构造

2.测测你的fft

算法：杨表

3.记忆

算法：线段树/分块+平衡树

2024.01.17

1.因数分解

算法：构造

2.诡意行商

算法：整体二分

3.树上最长上升子序列

算法：点分治+启发式合并

2024.01.19

1.九转大肠

算法：树形dp

2.原本味道

算法：min+矩阵

3.顶级厨师

算法：动态规划dp

2024.01.21

1.郊游

算法：01trie

2.雪仗

算法：多源最短路

3.闪耀

算法：根号分治

2024.01.22

1.虚化

算法：万能欧几里得

2.灵能潮汐

算法：递归+动态规划dp

3.优雅队列

算法：凸包

2024.01.24

1.桜花抄

算法：园方树

2.コスモナウト

算法：HALL定理+线段树

3.秒速5センチメートル

算法：容斥+卷积

2024.01.28

1.游戏

算法：博弈论+线段树

给出一个 \(01\) 序列，我们定义在一个长度为 \(m\) 的 \(01\) 序列中的一次操作为：选择一个点 \(i(a_i=1)\) 并删除 \(m-i+1\) 这个点，组成新的长度为 \(m-1\) 的序列。

实现以下两种操作：

• 给定 \(k\) 个区间转换为 \(k\) 个序列，\(Alice\) 和 \(Bob\) 轮流操作，先无法操作者输。
• 对区间 \((l,r)\) 取反。

首先从博弈出发，发现在一个序列中只有选到的位置在正中心时，才会删除本身，否则只会删掉数的数量较多的一边。所以对于每个合法位置一直操作只会使左右平衡最后消失，发现每个序列最左边的 \(1\) 和最右边的 \(1\) 是到达平衡状态操作最多的合法点，所以只需要找到这两个点即可计算出一个序列固定的操作次数，最后就转化为了一个简单的 \(nim\) 游戏，再用线段树简单维护一下区间取反即可，时间复杂度 \(O(n \log n)\)。

2.连通

算法：高位差分

3.C位

算法：线段树分治+递推

2024.02.16

1.寄

算法：树形dp

2.摆

算法：杜教筛

3.润

算法：容斥+卷积

2024.02.17

1.函数疆土

算法：基环树+动态规划dp

2.真夏飞焰

算法：后缀数组SA

3.随机树生成器

算法：生成树

2024.02.19

1.众数

算法：Set+启发式合并

2.火柴

算法：边双

3.疑问

算法：动态规划dp

2024.02.20

1.送信

算法：计数

2.饺子

算法：树状数组+Hash

3.机关

算法：递推

2024.02.22

1.十

算法：线段树

2.二十

算法：旋转卡壳

3.七十

算法：带状高斯消元

2024.02.23

1.圣诞树

算法：动态规划dp

2.过河

算法：二分图

初始有 \(n\) 头猪，农场主需要将他们送到对岸，有 \(m\) 个三元组 \((a,b,c)\) 表示在农场主不在的情况下这三头猪不能待在一起，求能否将全部猪送到对岸。

发现第一次一定会运走一头所有三元组都有的猪，然后我们将剩下的二元组两两连边，那么每次带去对岸的猪不能与对岸的猪有边，但我们发现带过去一条有边的猪后，会将先前的一头“万能猪”带回去，再带一头猪到对岸，此时两边的猪所连的边一定构成二分图！

此时问题就化简成了：一张图删掉两个点是否能成为二分图，两个点显然是不好处理的，我们先枚举一个点，于是就需要一种判断删一个点是否能成为二分图的方法：

通常判断一个图是否是二分图我们会使用 \(bfs\) 黑白染色，其本质为二分图没有奇环，所以删掉的点一定在所有奇环的交集中，这对应了第一个条件：一个合法点需要在所有奇环的交集中。然而还有两种特殊情况我们需要考虑，第一种是当一个奇环与一个偶环有交时，偶环通过奇环会产生一个新奇环，删掉一个点断掉了奇环，不一定能断掉新奇环，这对应了另一个条件：一个合法点不能同时在一个奇环和一个偶环的内部（不包括两环的端点）。第二种特殊情况为当前点 \(u\)，虽然同时在一个奇环和一个偶环内部，但两个环不来自同一颗子树，删掉 \(u\) 同样可以同时断掉两环，于是最后一种条件：一个不合法点覆盖它的奇环与偶环必须来自同一子树。

整理条件后为：

• 合法点必须在奇环的交集中。
• 合法点不能被来自同一子树的奇环和偶环覆盖。

具体维护细节为我们记 \(f_x,g_x\) 分别表示越过 \(x\) 的奇环/偶环的最小深度：

对于一条 \(dfs\) 树上的返祖边 \((u,v)(dep_u>dep_v)\) 边转移：

if ((dep[u] - dep[v]) & 1) f[u] = Min(f[u], dep[v]);
else g[u] = Min(g[u], dep[v]);

对于一个点 \(x\) 和其儿子 \(v\) 判断是否能作为合法点：

if (f[v] < dep[x] && g[v] < dep[x]) cant[x]=1;

最后这道题就成了一道板子啦！时间复杂度 \(O(n^2)\)。

3.点对游戏

算法：点分治

2024.02.25

1.签到

算法：容斥

2.数据结构

算法：带权重心

3.爆搜

算法：状压dp

2024.02.26

1.博弈

算法：博弈论+动态规划dp

2.排列

算法：模型转化+动态规划dp

给定一个 \(n\)，求所有 \(1 \le a < b \le n\) 的二元组 \((a,b)\) 的一个排列，满足对于 \(1 \le a < b < c \le n\) 的 \((a,c)\) 必须在 \((a,b)\) 和 \((b,c)\) 之间，再给出 \(m\) 条限制，使 \((a,b)\) 在 \((c,d)\) 前面，求满足条件的合法排列数。

神仙思路题！首先阶乘暴力显然无法接受，于是我们需要分析这个满足条件的排列的一些性质。发现 \((a,c)(a,b)(b,c)\) 这种条件很眼熟，\(Floyd\) 算法！当然我们也可以叫它传递闭包，这种条件所带来的性质即为：在一个区间中，如果有 \((a,b)\) 和 \((b,c)\)，那么一定有 \((a,c)\)，我们称这样的性质为传递性。

接下来我们将每个二元组 \((x,y)\) 化为一条边，发现这样的图也同样具有传递性，即 \(a \to b\) 且 \(b \to c\) 则 \(a \to c\)，实际上就是传递闭包。因为这个图在加边的过程中始终具有传递性，所以它的前缀子图一定也具有传递性，所以我们有了一个基本的思路：统计从无边图到完全图的合法加边方案数。

这时候一个难题扑面而来，图的量级是 \(n\) 的平方阶乘级别的，如何枚举呢？接下来最神的点来了，我们要借助排列的性质，我们将每一个前缀子图和每一个 \(n\) 阶排列对进行双射，为什么能这么做呢？我们把排列中的逆序对看成前缀子图中的边，发现逆序对同样具有传递性！接下来的操作就比较简单了，我们枚举每一种前缀子图，也就是每一种排列，每次对当前图 \(S\)，交换两个相邻的数增加一个逆序对，即求出添加一条边后的状态 \(T\)，再将 \((S,T)\) 进行连边，最后统计无边图到完全图这个 \(DAG\) 的路径条数即可，至于 \(m\) 条限制，只需要在每次加边 \((c,d)\) 时判断 \((a,b)\) 是否已加即可，可以用裴蜀定理对每个排列进行编号以方便 \(dp\)，时间复杂度 \(O(n!n)\)。

3.子段和

算法：线段树

2024.02.28

1.鸭棋

算法：模拟

2.激光切割机

算法：凸包+树状数组

3.散步

算法：动态规划dp

2024.02.29

1.A

算法：最小割

2.B

算法：动态规划dp

3.C

算法：扩展欧拉定理+线段树

2024.03.03

1.选拔士兵

算法：线段树+单调栈

给出两个长度分别为 \(n\) 和 \(m\) 的编号序列和权值序列 \(A,B\)，要求在两个序列各选一段区间（可以不选），使得两区间没有重复的编号且最大化权值和。

我们发现最简单的情况即为全选其中一个序列，所以我们的方案要更优的话，需要至少一个序列选的区间权值和为当前序列的一半以上，于是我们找到一个前缀和刚好大于 \(\frac{sum}{2}\) 的位置 \(p\)，因为需要满足前面的条件，所以 \(p\) 这个点是必选的。

这时我们在 \(A\) 中就固定了一个点，一个显然的做法即为：在 \(B\) 中选择一段区间，并将区间中的编号对应在 \(A\) 中的点进行标记，再将 \(p\) 点进行左右拓展即可。然而直接枚举区间的复杂度也是显然无法接受的，考虑只枚举 \(B\) 所选区间的右端点 \(r\)，尝试对每个 \(l\) 统计答案，发现如果出现了一个 \(r\) 的编号在 \(A\) 序列中位置为 \(k\)，如果 \(k<p\) 那么选择这个点会限制 \(p\) 能统计到的左端点，右端点同理。发现这两者是严格递增/递减的，所以用线段树统计答案，再用两个单调栈分别维护左端点和右端点，单调栈只需要支持出栈的撤回和入栈的修改即可。

2.草

算法：点分治+分讨

3.集结

算法：欧几里得坐标+切比雪夫坐标

给出 \(n\) 个二维平面上的点，要求恰好经过 \(m\) 次上下左右的移动，能到达同一位置的方案数。

非常的巧妙，我们将原本的欧几里得坐标转换为切比雪夫坐标，此时 \((x,y) \to (x+y,x-y)\)，并且我们的四种移动分别变为了 \((+1,+1)(+1,-1)(-1,+1)(-1,-1)\)，相当于每次在一个点的横坐标和纵坐标上分别加一或减一，这样的好处就是完全把横坐标与纵坐标的影响分开了，直接枚举最后横坐标到达的位置和纵坐标到达的位置乘法原理计算即可。

2024.03.05

1.跳！跳！跳！

算法：状态压缩+并查集

2.翻！翻！翻！

算法：构造

3.卷！卷！卷！

算法：生成函数+分块

2024.03.07

1.game

算法：线段树

2.count

算法：组合数学+动态规划dp

3.ciallo

算法：线性基

给出 \(n\) 个点的带权树，回答 \(q\) 组询问，每次给出 \(x_i,y_i,l_i,r_i\)，需判断在树上与 \(x_i\) 距离小于 \(l_i\) 和大于 \(r_i\) 的点是否能选任意个出来使得其亦或和为 \(y_i\)。

选若干个权求亦或可行值/k大值是线性基的常规操作，考虑将小于 \(l_i\) 和大于 \(r_i\) 的线性基分开处理，最后再合并到一起。如果问题在序列上，直接使用线段树维护区间线性基是 \(O(n \log^3 V)\) 的，我们可以使用一种维护区间线性基的方法，使得其复杂度降至 \(O(n \log V)\)，具体为对于线性基的每一位再记一个值 \(pos_i\)，如果遇到已经填过的 \(p_i\)，就可以根据需要比较 \(pos_i\) 的大小来进行替换。

对于树上一个点的线性基我们考虑分两部分维护，子树内和子树外，子树内是好处理，从下往上合并即可，重要的是子树外的部分该如何处理，于是我们看每次向子树移动需要做什么，因为需要处理完子树 \(v\) 以外的数，所以我们需要进行三步操作：

• 将当前点 \(u\) 的权值加入线性基。

• 将 \(u\) 对于 \(v\) 的前缀子树加入线性基。

• 将 \(u\) 对于 \(v\) 的后缀子树加入线性基。

具体操作如下图：

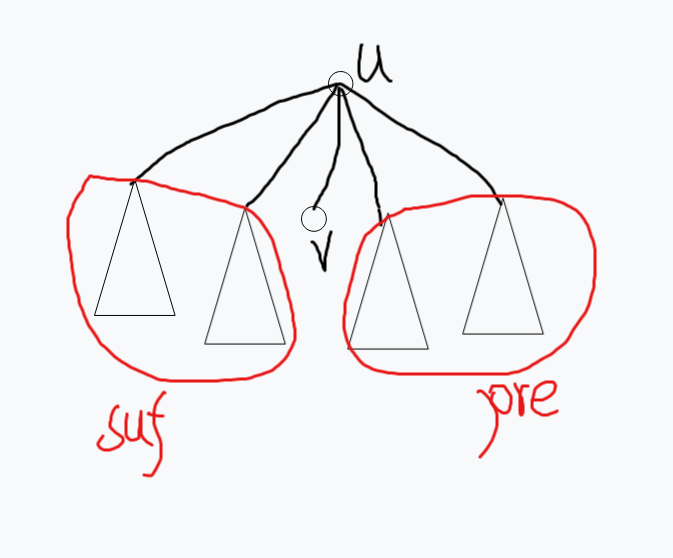
将这三部分加入以后即可对于每个点维护全图的线性基，因为我们有小于和大于两部分，所以每个点实际维护了两个线性基，因为他们的 \(pos\) 比较是不一样的。

最终的时间复杂度为 \(O(n \log^2 V )\)。

2024.03.10

1.采购蔬菜

算法：背包+k短路

2.随机逆序对

算法：分类讨论

3.游戏

算法：定期重构

给出 \(n\) 个关卡，每个关卡需要在 \([l_i,r_i]\) 中至少 \(k_i\) 个关卡解锁后才会解锁，求最后解锁的关卡数。

一个比较好想的暴力是给线段树的每一个节点维护一个 \(set\)，把每个区间限制打在对应的至多 \(\log n\) 个节点，对于每一个删掉的点，暴力遍历线段树上包含的区间，时间复杂度为 \(O(\sum k_i+n \log^2 n)\)。

发现唯一不能接受的复杂度就是 \(\sum k_i\)，考虑有些限制不用太早打到线段树上，所以我们考虑一种定期重构，即一共重构 \(\sqrt n\) 次，每次将 \(k_i \le \sqrt n\) 的限制打到线段树上，这样均摊下来的复杂度能减少到 \(O(n \sqrt n+n \log^2 n)\)，如果将 \(set\) 换成链表还可以变成 \(O(n \sqrt n+n \log n)\)。

2024.03.12

1.放进去

算法：高维前缀和

2.生成树传说

算法：贪心

3.前置知识

算法：贪心

2024.03.14

1.液晶显示器

算法：迪利克雷生成函数+杜教筛

2.军用交换机

算法：虚树+链表

3.迷雾

算法：动态规划dp