2023解题报告(CSP-S前)

2023.06.17

1.b

算法：KMP自动机+动态规划dp

给出两个字符串$S,T$，问至少删去中多少个字符，才能使得$T$不在$S$中出现。

构造状态$f_{i,j}$表示考虑$i$中前$j$个字符，到达匹配到自动机状态$j$需要删除的最少字符，状态转移式即为:

$f_{i+1,j}=f_{i,j}+1$
$f_{i+1,ch[j][S[i+1]]}=f_{i,j}$

此处附带转移代码：

//lent:T的长度
if(j!=lent) 
	dp[i][j]=max(dp[i][j],dp[i-1][j]);
if(ch[j][s[i]-'a']!=lent) 
	dp[i][ch[j][s[i]-'a']]=max(dp[i][ch[j][s[i]-'a']],dp[i-1][j]+1);

2.乘积筛

算法：记忆化+数论分块

对于两个长度为$N$和$M$的序列$A$和$B$，给出一个数$C$，求：

$\sum\limits_{1 \le x \le N,1 \le y \le M,px+qy=C}a_xb_y$

对于这道题我们可以枚举中$p,q$较大的一个对应的数组的下标，

单组询问的复杂度即为$O(\dfrac{n}{max(p,q)})$，然后考虑两种情况：

当$max(p,q) \ge \sqrt{n}$ 时，暴力枚举即可。
当$max(p,q) < \sqrt{n}$ 时，可以记忆化搜索，这样最多需要计算 $n\sqrt{n}$ 次。

3.国战

算法：整体二分/主席树

一棵树，上面的点有一个战斗力与威望值，如果我们的战斗力大于等于点就可以获得威望值，有$q$个询问，每次给一个起点和重点和期望威望值，问至少要多少战斗力才能达成这个期望威望值。

可以主席树维护每个点到根节点路径上关于 $v_i$ 的值域线段树，线段树内叶子点权记为对应的 $p_i$ 的和。查询操作看成在$3$棵线段树上二分，即到根$s_i$到根的线段树，$t_i$到根的线段树，以及$lca(s_i,t_i)$到根的线段树，直接在线段树上二分，时间复杂度可以做到$O(n~log~n)$。

4.烤串

算法：主席树

2023.07.03

1.最小基因序列

算法：二分哈希

一个只由 $A$、$T$、$C$、$G$ 组成的字符串，可以进行一次操作，选取一段翻转并把 $A$ 与 $T$ 互换，把 $C$ 与 $T$ 互换，求变换后的字符串字典序最小。

这道题可以先找到字符串中第一个不是$A$的位置，这个位置注定被后面的一个变换后的字符所替代，于是再找到后面可以替换它并且保证最大的字符位置，于是会得到$x$组区间$(l,r_i)$，再按照转换后的基因序列对这些区间的字符串进行排序，可以用哈希二分或后缀数组解决这个问题。

2.等差数列

算法：逆元+环

给定一个长度为$N$的序列$A$以及一个质数$M$，序列$A$内的元素两两不同。询问能否将序列$A$重新排列成一个序列$B$，使得序列$B$在模$M$意义下是一个等差数列,求序列$B$的首项和公差。

小于$M$的这$M$个数以$d$为公差组成了一个环，我们任意找到两个数字，他们的差记为$Kd$，即公差的$K$倍，需要分两种情况讨论：

$2N \le M$ 直接选取两数之差找多少数不在$Kd$为差的环内，即为$K$。
$2N > M$ 选取两数之差在原环的补集中找在环内的数，即为$K$。

3.策略游戏

算法：记忆化搜索+公因数

给出两个数 $a,b$，每次可任意完成以下三种操作：

将 $a,b$ 同时减一
将 $a,b$ 同时加一
将 $a,b$ 同时除以共同的质因数

问最少操作多少次能使其中一个数变成 $1$。

记两数之差为$d$，且$(a,d)$表示手上的数为$(a,a+d)$，考虑每次$(a,d)$进行第三种操作时会变成$(\left\lfloor\dfrac{a}{g}\right\rfloor,\dfrac{d}{g})$或是$(\left\lceil\dfrac{a}{g}\right\rceil,\dfrac{d}{g})$，其中$g|d$。

因为质因数的量级较小，所以只需要枚举状态然后记忆化搜索就行了。

2023.07.05

1.舞

算法：贪心

给定一个长度为$N$的正整数序列，你需要对序列内数末尾添加数字的方法使序列严格单调递增，求最小添加数字的次数。

典型的模拟贪心题，可以维护上一个数字的值然后贪心地让新的数字最小。先比较高位，如果高位相等，则查看低位能否加一，可以的话新数就是旧数加一。否则多加一位。如果高位不相等，新数小于旧数就往后补$0$至补齐，否则多补一位。注意所有的加$0$都需要记录，暴力加的话时间复杂度不支持。

2.此后

算法：基数排序+链表

有$N$个元素，每个有两个属性$(a_i,b_i)$。要求把他们划分成两个非空集合$S,T$，使得每个元素恰好在一个集合中，并且最小化$\left| max_{i \in S }a_i-max_{j \in T}b_j\right|$

我们可以排序之后，从大到小枚举$a$，使用链表维护数组$b$。由于我们枚举$a$的时是单调的，所以不需要将$a$扔进链表，维护$b$的链表支持删除操作即可。最后再利用基数排序减少常数，这道题就迎刃而解了。

3.选择

算法：图论+偶环

有$n$个二元组，每个二元组给出两个元素$(a_i,b_i)$，每个二元组只能选取一个元素，求当元素和为$2N$的倍数时，选取的元素集合。($n$为奇数，且题目保证有解)

我们将数字分成$N$组,$i$和$i+n$分成一组，我们从每一组中选出一个数字，那么最后就一定会选出一个$n$的倍数，由于$1-2n$的和是的奇数倍，要么我们选出的数字，要么我们没选的数字，他的和是$2n$的倍数。

可以选择写$dfs$,让$a_{i,1}$和$a_{i,2}$连边，$i$和$n+i$连边，每个点度数为$2$，图中一定只有偶环，对于每个环再搜一遍就行了。

2023.07.07

1.异或平方和

算法：位运算+推式子

求 $\sum\limits_{i=1}^n \sum\limits_{j=1}^n (a_i \oplus a_j)^2$

可以通过按位计算推导公式，最后会变成：

$\sum\limits_{k=1}^L \sum\limits_{l=1}^L 2^{k+l} (\sum\limits_{i=1}^n \sum\limits_{j=1}^n[f_{i,j,k}==1 \&\& f_{i,j,l}==1])$

其中 $f_{i,j,k}$ 表示的是 $a_i \oplus a_j$ 二进制上的第 $k$ 位。

2.除雪

算法：树形dp+贪心

小可可的院子可以看作一棵 $n$ 个点的树。

冬天，这棵树的每一个点上都堆积了深度为 $a_i$ 的雪。不过小可可有一台铲雪机，他每一次可以开着铲雪机从一个点沿着最短路到另外一个点，让经过的点的雪的深度减一。由于铲雪机非常暴躁，所以如果地上没有雪，这辆车甚至会把地皮带走。

因此他不能开车经过没有雪的点。由于铲雪很麻烦，所以小可可想知道，最少要开几次铲雪机才能把雪扫完呢?

我们可以先求每个点单独减,这样要花费权值之和的次数。然后我尝试把某些减合并,对于一个点,我们把它分为 $a_i$ 个权值为$1$的点，一个点分成的点就可以向至多两个相邻的点连边(因为每次只能铲一条链)，于是答案就变成了最大匹配(不是二分图最大匹配)，树形$dp$统计合并的结果即可。

3.天堂之战

算法：倍增

给出$n$个星系，每个星系的位置为$a_i$，保证$a_i>a_{i-1}$。

共$q$次袭击，一次袭击开始时对方的舰队可能会位于$(l,r)$内的任意位置开始，朝数轴上的轴正方向移动，结束于$(l,r)$内的任意位置。舰队会攻击所有路过的星系（包括起点和终点）,同时每次移动只能到距离$\ge d$的星系。

对方会合理规划袭击的路线，使得所有舰队移动都使用星门穿梭。在满足上述条件的情况下，对方还会最大化攻击星系的数量。

对于每次袭击，请求出你在$(l,r)$内可以不设防的星系数量。

这道题我们可以先预处理出每个星系可以到达的最近的下一个星系，并且进行倍增的预处理，然后求出两个序列$A,B$：

$A$序列表示从第$l$个星系开始，最多能到达的星系的下标序列。
$B$序列表示从第$r$个星系开始，最多能到达的星系的下标序列。

假设序列的长度为$len$，并且容易证明到每个$(A_i,B_i)$区间都无法被攻击，
于是答案贡献式子即为：

$\sum\limits_{i=1}^{len}(B_i-A_i)$，就于先前的倍增预处理，复杂度可以降低到 $O(n$ $log$ $n)$。

2023.07.10

1.城市天际线

算法：并查集

给定$n,m,X$，请构造一个$n$个点$m$条边的简单有向图，满足其恰好有$X$个强连通分量，还有额外的$Q$个限制需要满足：第$i$个限制要求编号为$a_i$的点与编号为$b_i$的点处于同一强连通分量内。

我们首先根据必须在一个强连通分量的点进行并查集，将所求的集合再从大到小合并成恰好$X$个集合，这样能满足$m$的上限最高。然后根据集合计算$m$的上下限，进行特判后输出集合组成的图就行了。

2.景点距离

算法：完全二叉树

给出一个$N$个点的图，同时$i(i > 1)$与$\left\lfloor\dfrac{i}{2}\right\rfloor$相连，支持两种操作：

删除一个节点的父边。
求多少组$(i,j)$的最短路径不超过$k$。

应注意到询问的$k \le 40$，正向减边的路径计算较为麻烦，于是我们选取将询问从后往前进行加边处理。考虑到这颗树非常特殊的结构完全二叉树，我们可以从根节点进行递归，统计路径数可以做到$O(n~log~n)$，具体操作即为将当前节点$x$，向$x \times 2$和$x \times 2+1$进行递归，记录每个路径长度的$siz_i$，表示到最短路径长度为$i$的节点路径数量，每次加边再在加边节点向上再递归一遍，这道题就解决了。

3.排列

算法：矩阵乘法

设$f(n)$为满足以下条件的序列$p$数量:

$p_1=1 \land \forall i < n,\left|a_i-a_{i-1}\right| \le 2$

求$T$组$f(n)$的值。

分类讨论$p_2$和$p_3$后，得到递推式：$f_i=f_{i-1}+f_{i-3}+1$，我们考虑换元去优化，令$g_i=f_i+1$,则原式变为 $g_i=g_{i-1}+g_{i-3}$，于是直接矩阵优化：

我们定义初始矩阵为$\begin{vmatrix}2&2&1\end{vmatrix}$ 即为 $(g_2,g_1,g_0)$，然后再根据递推式推出转换矩阵:
$\begin{vmatrix}1&1&0\\0&0&1\\1&0&0 \end{vmatrix}$，最后进行$n$次转移再加上矩阵快速幂优化这道题就迎刃而解了。

($ps$：注意数据会卡常，需要预处理转移矩阵的次方才能通过)

2023.07.12

1.生命游戏

算法：BFS+二分答案

游戏初始有若干格子有生命存在，如果在某一秒一个不存在生命的格子上下左右任意一个格子存在生命，那么这个格子下一秒也会存在生命。已经存在的生命不会死亡。

现在小可可想让生命摆成一种特定的图案。他想知道，初始时如果他放置可以任意放置生命，那么最多经过多少秒，有生命的格子才会摆成小可可想要的图案呢？（必须在某一秒要摆出来才行）

表示要求这个格子有生命，.表示要求没有。

我们可以先处理每个 $#$ 到 $.$ 的距离，然后二分答案最大的时间，在可以满足时间去扩张的点上做标记，再进行一遍$BFS$，判断是否和原图相符合就行了。

2.Bajka

算法：动态规划dp+前缀和

给出两个字符串$S,T$，求在$S$上做操作后写出$T$的最小步数，两种操作分别为：

向左或向右移动一步并写下字母。
移动到相同字母的位置，但并不会书写

其中初始可以在任何位置上，并先写下初始位置上的字母。

可以$dp$，首先设计$dp$状态为$f_{i,j}$表示我们现在位于字符串$S$的第$i$个位置，下一个要写的字符为$T_j$时需要的最低代价，于是考虑两种转移：

左右转移$dp_{i+1,j+1}~or~dp_{i-1,j+1}=dp_{i,j}$，需 $S_{i+1}=T_{j+1}~or~S_{i-1}=T_{j+1}$。
同种字母转移$dp_{i,k}=dp_{i,j}$，需$S_k=S_j$，可以用前缀和优化这一步骤。

于是枚举$j$为$O(m)$，转移为$O(n)$，总复杂度$O(nm)$。

3.序列修改

算法：分类讨论+Set

定义一个长度为$n$的序列$a$的频度序列$c$，$c_i$表示$a_1,a_2,......,a_i$中数的种类数，定义$c$序列的代价：
$worth(c)=\sum\limits_{i=1}^{n}c_i \times i$

现在可以修改$a$序列中至多一个数，求$worth(c)$和修改数之间的绝对值的最小值。

可以发现，对于每一种数第一次出现的时候，将先前的数$a_j$修改为该数$a_i$，对于答案的贡献为 $\left| a_i-a_j \right|-(n-i+1) \times (n+i)/2$，即为两数绝对值减去$i$到$n$差为$1$的等差数列的和，于是我们用$Set$来维护每个$a_i$的前驱后继，再进行答案的统计。

最终时间复杂度可以降到$O(n$ $log$ $n)$，需要特判$Set$二分时迭代器是否触及边界。

2023.07.14

1.valk

算法：字典树+博弈论

$N$和$E$正在玩一个特殊的游戏。这个游戏是在一张最开始为空白的纸上进行的。在每一个人的行动回合内，这个人会在这张纸上当前的单词后面加入一个字母。她们会轮流行动，而$N$先手行动。

操作者必须保证这样一个条件：在添加完一个字符后，整张纸上的单词必须是操作人最喜欢的歌曲的一个单词的前缀。如果不满足条件，进行这个操作的人就输了。

你的问题是，如果两个人都采取最优策略，那么谁会获得最后的胜利。

考虑先将两人喜欢的曲名建成一颗字典树，并记录归属于他们的边以及公共的边，在字典树上遍历时，如果一方无法再走下去，则另一方有必胜策略。所以只需要在字典树上进行一遍便利，如果$N$有必胜策略就输出$N$，否则输出$E$。

2.selotejp

算法：轮廓线dp

$M$先生的手中有一个大小为$n \times m$的棋盘，每一个棋盘的格子大小都是 $1 \times 1$。不幸的是，有一些格子已经弄脏了，需要重新粉刷。

一次粉刷可以粉刷同一行或者同一列的某一些格子。但是$M$先生不允许粉刷到不需要粉刷的格子。你的任务是，求出最少需要粉刷多少次，才能够把棋盘上的脏格子全部粉刷一遍。

轮廓线dp是状压$dp$的一种，可用于在图上进行横向和竖向的情况转移。

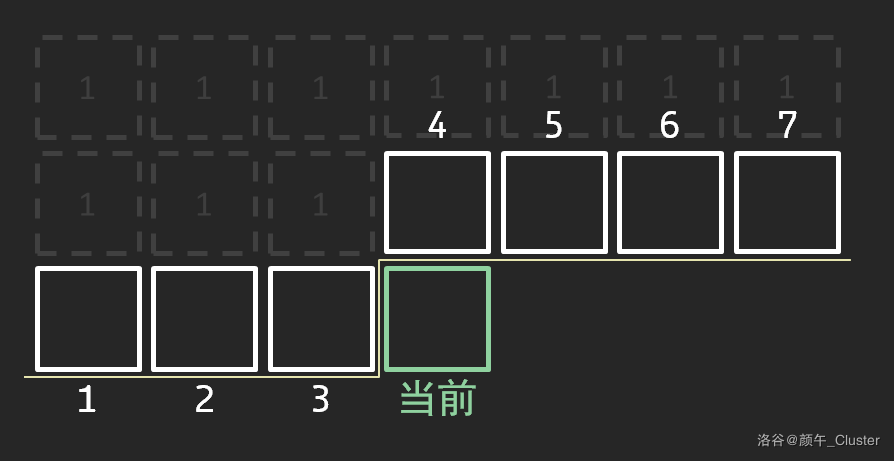
如图所示，图中绿色格子为$\color{LimeGreen}\text{当前}$推到的格子。那条金黄色亮闪闪的线就是$\color{Goldenrod}\text{轮廓线}$。

我们用格子所在的列数，来给轮廓线上方的白色格子编号。编完号后即可二进制状态压缩，用$1$表示被覆盖，用$0$表示未被覆盖。于是转移就很显然了，对于当前位置如果需要被覆盖，我们可以向左或者向上合并，否则直接$+1$进行覆盖。

我们定$i,j$为当前位置，$ti,tj$为需要覆盖的对象位置，$k$为枚举的轮廓线状态，则状态转移式如下：

if(tj>1&&!(k&1<<m-1)&&c[i][j]=='#') 
    dp[ti][tj][k>>1]<-dp[i][j][k];
else 
    dp[ti][tj][k>>1]<-dp[i][j][k]+1;
    
if(ti>1&&(k&1)&&c[ti-1][tj]=='#') 
    dp[ti][tj][(k>>1)+(1<<m-1)]<-dp[i][j][k];
else
    dp[ti][tj][(k>>1)+(1<<m-1)]<-dp[i][j][k]+1;

到这里这道题就完成了，当题目对于轮廓线$dp$的状态有空间限制时，我们还可以对$dp$数组进行滚动处理，以达到降低空间复杂度的目的。

3.papricice

算法：LCA+Set

给出一棵树，需要在一棵树上切掉两条边，使这棵树被切成的三部分中的节点数的最大值和最小值差最小。

我们可以分类讨论，先枚举其中一个点$x$，$x$的父边作为第一刀的位置，在剩下的树中找一个节点$y$，使得$siz[y]$尽可能接近$\frac{N-siz[x]}{2}$。

于是我们可以在$dfs$过程中把每个计算过的点的$siz$值扔进一个$set$里然后二分，但对于$y$为$x$的祖先节点时，贡献应该是$siz[y]-siz[x]$，所以我们可以在$dfs$过程中把当前节点的祖先节点放进一个栈里，其余的节点放进另一个栈里。在计算放祖先节点的栈统一减一个$siz[x]$就好了。

2023.07.17

1.patkice

算法：模拟

根据符号模拟鸭子漂流的四种路线，再求出其中最短的一条。

纯模拟，注意不可去的地方的标记。

2.内鬼

算法：状压dp+分层最短路

3.诡意行商

算法：整体二分

2023.07.19

1.原题

算法：数论

给出 $n$ 和 $\varphi (n)$，对 $n$ 分解质因数。

因为 $n \le 10^{18}$，所以先将 $\le 10^6$ 的质因数筛出，最终会剩下 $1$ 个或 $2$ 个质因数。于是设出剩下的两个数$p,q$，考虑用 $\varphi (n)$ 与 $n$的关系：

$\varphi (n)=(p-1) \times (q-1)$
$n=p \times q$

因为 $n$ 和 $\varphi (n)$ 是已知的，所以解出二元二次方程就可以了。

2.撰写博客

算法：动态规划dp+KMP

给出一个长度为 $n$ 的字符串 $S$，和删除每个位置的代价 $v_i$。要求 $S$ 中不能出现 $m$ 个字符串 $T_1,...,T_m$，求满足条件的最小代价。

因为删除一个数后前后的两段将不会有任何联系，所以考虑分段dp，可以先预处理以 $i$ 结尾的最长的不包含任何模式串的区间 $[l_i,i]$，这里用 $Kmp$ 即可。

最后我们进行 $dp$ 转移：

\[dp_i=min(dp_i~,~j \in (l_{i-1}+1,i-1))+v_i \]

单调队列即可。

3.顶级厨师

算法：动态规划dp

2023.08.07

1.骰子游戏

算法：亦或

给出 $n$ 和 $k$，需要构造出 $n$ 个骰子满足：

每个骰子的六个面数字各不相同且范围在 $0$ 到 $10^6$。
每个骰子随机扔出的数字的亦或和为 $k$ 的倍数。

这道题需要我们在二进制的亦或条件下满足倍数关系，于是我们考虑转化。原题目中 $k \le 60$，所以我们可以将数字转化成$64$进制，这样将骰子上的六个数在二进制下分为了六个区块，亦或时不会互相影响，于是最终我们只需要令每个骰子上的数为$0,d,64d,65d,4096d,4097d$ 就可以了。

2.裁剪彩带

算法：动态规划dp

给出一个非负整数序列，定义一个子序列的$mex$为该子序列未出现的最小的非负整数，现在可以把原序列分割成若干个子序列，求最大的$mex$和并且列出分割方案。

首先定义$dp_i$表示处理到第$i$个数字的$mex$最大值，我们可以枚举$i$，然后从$j(j \le i)$实现$O(n^2)$的转移。然而我们发现数字大小$V \le 20$，所以我们对于每一个$i$，枚举$0$到$20$这些数最近出现的位置，数字位置可以动态记录，于是状态转移方程即为：

$dp_i=max(dp_i,dp_{last_V-1}+V)$

其中 $last$ 为数字 $V$ 上次出现的位置，最后的分割方案我们可以用一个数组 $g$ 来记录，对于每次可以转移的情况记录 $g_i=last_V$，最后从 $g_n$ 遍历一遍就大功告成了。

3.挑战 NPC

算法：最大流

给你 $n$ 个点，$m$ 条边的有向图，求出若干不相交的环使每个点都被经过，或无解。

因为环上的每个点入度和出度都为$1$，所以我们可以用网络流来判断有向图是否可以用环来全部遍历一遍。我们可以先从源点向第一层的每个点连边，同时从第二层的每个点向汇点连边，再根据题目给的有向边将第一层和第二层的点连接（每条边的容量均为1）。

下图为一种有解情况，我们发现当一个有向图能被若干个环遍历完所有点时，它的最大流即为点的个数 $n$：

反之当最大流小于有向图点数时，方案无解。

所以我们跑一遍最大流 $Dinic$ 既可以判断是否有解，最后我们再将残量网络中被跑过（流量变为0）的边连成环，$dfs$一遍记录就行了。

2023.08.09

1.genshin

算法：三分法

对于 $n$ 个人，每个有自己的位置 $p_i$，速度 $w_i$ 秒每米，和听力范围 $d_i$，求在任意位置中，所有人移动并听到该位置的声音时，所有人移动时间和的最小值。

因为对于每个人到任意位置的时间 $t$ 是一个分段函数，即：

当 $x < p_i-d_i$ 时 $t=w_i \times (p_i-d_i-x)$
当 $x > p_i+d_i$ 时 $t=w_i \times (x-p_i-d_i)$

所以答案的坐标一定在某个人的听力范围的端点上，然后我们可以用三分法枚举位置，再 $O(n)$ 暴力计算贡献，最终时间复杂度为 $O(n~log_3~p)$

2.arknights

算法：动态规划dp

给出一个 $n \times n$ 的国际象棋棋盘，要求放置 $k$ 个象，求象互不攻击的方案数并取模。

我们首先观察一个 $5 \times 5$ 的棋盘：

在国际象棋中，黑格象和白格象互不干涉，所以我们分为黑白两种情况讨论。对于所有的黑格，斜线显然不好处理，于是我们将整个棋盘旋转 $45$ 度，即为：（白格同理）

$~~~~~~~~~~~~$

我们发现对于翻转后的图，只要对于每一行每一列只放一个象，最后就不会互相干涉，所以我们考虑 $dp$：

$dp_{j+1}=dp_{j+1}+dp_j \times (i-j)$

其中 $dp_j$ 表示已经放了 $j$ 个象的方案总数，$i$ 表示当前枚举到的行数有多少列，转移大意为在第有 $i$ 列的一行再放一个象，因为先前已经放了 $j$ 个象，又因为每列只能放一个象，所以最终的列数应该为 $i-j$。

最后再分奇偶讨论一下 $n$，将黑白格的情况用乘法原理合并，答案就出来了。

时间复杂度为 $O(T(nk+k^2))$，注意多测要清空。

3.arena

算法：容斥+递推

给出一个长度为 $n$，值域为 $0$ 到 $n-1$ 的排列，求多少组区间 $S$ 满足 $mes(S) \le med(S)$，其中：

$mes$ 表示区间中出现的最小的非负整数。
$med$ 表示 $S$ 的第 $\left \lfloor \frac{\left | S \right | +1}{2} \right \rfloor$ 项的值。

我们关注排列这一信息后，发现 $mes$ 会比 $med$ 更好处理，因为每个数只会出现一次。所以我们可以先枚举 $mes$ 的值用桶存下每个数的位置，然后就可以表示满足 $mes$ 某个值的最小区间。

但是 $med$ 该如何处理呢？我们借助 $mes$ 的性质，当 $mes=d$ 时，区间中必定会包含 $0$ 到 $d-1$ ，所以区间的其它数一定 $\ge d$，那考虑区间长度为 $d \times 2$ 或者 $d \times 2 -1$ 的数量就行了，$d \times 2 -2$ 在 $d-1$ 就已经计算了，不必考虑。然而题目要求的是 $mes \le med$，我们的区间满足的是 $mes > med$，简单容斥即可。

4.rail

算法：哈希+递推

定义一个两个字符串形似 $AB$ 和 $BA$ 时（$A,B$均为字符串），称它们的关系为循环相同（例如：$ababba$ 和 $abbaab$）。现在给出一个字符串 $S$，求最长的 $L$ $(L \le \left \lfloor \frac{n}{2} \right \rfloor )$ 满足 $S$ 的 $L$ 前缀和 $S$ 的 $L$ 后缀循环相同。

我们可以把这个字符串拆分成 $ABSBA$，我们枚举 $A$ 时，发现 $BSB$ 无法比较，也没有什么办法去枚举最长的 $BSB$，所以我们考虑一下去转换枚举顺序，把 $BSB$ 再拆成 $aBcSaBc$。如果我们把 $A$ 扩大，那就变成了 $BcSaB$，于是我们就需要去 $B$ 里找一个 $a$ 还要找一个 $c$，虽然不知道 $a$ 和 $c$ 是否相等，但是我们的长度肯定会减少 $2$，因此我们只需要去比较 $2$ 个字符，此处用 $Hash$ 处理即可。

设$f_i$为我们 $A$ 的大小为 $i$ 时的 $B$ 最大为多少，于是发现了一个递推式：

$f_{i+1} \ge f_i-2$

考虑枚举顺序，可以从中间开始，向外扩展，递推就更方便了。根据递推式所得：我们最多会比较 $2n$ 次，所以时间复杂度为 $O(n)$。

2023.08.11

1.perm

算法：动态规划dp+容斥

设 $Q(S)$ 为排列 $S$ 的逆排列，即：

$Q_{S_i}=i$

求长度为 $N$，满足 $S<Q(S)$ 的序列数量。

首先我们发现，对于一个序列的逆序列，因为 $S=Q(Q(S))$，所以只要是 $S \ne Q(S)$，他们的字典序关系是相反的，总有一方字典序小于另一方，会增加 $1$ 的贡献。

于是我们考虑容斥，将所有 $S=Q(S)$ 的方案数找出，我们设长度为 $i$ 的这种情况的数量为 $f_i$，容易发现，如果所有轮换大小不超过 $2$，那么组成的排列的逆排列就是自己，即为：

$f_i=f_{i-1}+(i-1) \times f_{i-2}$

最后对于每种长度 $i$ 进行容斥即可（序列贡献会被计入两次）：

$\sum_{i=1}^{n} \frac{(i!-f_i)}{2} $

2.tree

算法：树+搜索

给定一个 $N$ 个点的树，每一个结点都可以是黑色或白色，每一条边的长度都为 $1$。

定义两个点的距离为两个点最短路径上边的条数，定义一棵树的价值，为同色点距离的最大值。

求在所有情况下，树的价值之和，并取模。

我们首先找到一条直径，设其长度为 $L$，两个端点为 $x,y$。此时枚举最大距离 $d$。显然，距离 $x$ 距离超过 $d$ 的所有点都必须和 $y$ 颜色相同，距离 $y$ 超过 $d$ 的所有点都必须和 $x$ 颜色相同，中间未确定的位置随机颜色即可。

到树上即可找出直径，记录每个点到两个直径端点的距离，从大到小枚举 $d$，将点分为三类计数即可。当 $min(dis_{x,i},dis_{y,i}) > d$ 时就非法了。

3.network

算法：圆方树

机房有 $N$ 台电脑，之间有 $M$ 条双向连接，构成一个联通的无向图。

需要删除一个点，保证三个点中任意两点无法连通。

在圆方树上稍微分类讨论一下可以发现，答案其实至多只有一个点。首先特判处理重复点问题，接下来发现，三个点一定要位于不同的三个点双才行。

可以考虑的点仅有三个点之间的 $lca$，这样的 $lca$ 至多只有两个，如果存在两个 $lca$，显然只可能是较深的那一个点。

同时，这个备选答案的点一定得是一个圆点，如果是方点也意味着无解。
至此这个题目就做完了，建圆方树求 $lca$ 即可。

4.lis

算法：动态规划dp+长链剖分

给定一个 $N$ 个点的无根树，每个点有一个标号$w_i$。

定义一条链 $(u,v)$ 的权值为按照从 $u$ 到 $v$ 的顺序把这条链的标号写下来之后，得到的序列的最长上升子序列长度。

你需要删掉一个点，使得剩下的链的权值的最大值最小。

2023.08.12

1.lock

算法：哈希

给出 $4$ 行 $N$ 列的密码锁数列，可以将每行任意左右平移。

判断是否能达成每一列的四个数的和相同的情况。

先求出所有数的和，判断 $sum$ 是否能被 $N$ 整除。

可以分为两组情况讨论，先将第一二行和三四行各分为一组，求出两组各 $n$ 种情况，其中对于一组的情况要将所有数 $v_i$ 变为 $ave-v_i$，于是对两组情况分别进行哈希（因为顺序枚举会超出时间复杂度，所以对于哈希比较需要复制一份在原串后），并记录下每组哈希的最小表示，最后进行比较即可。

2.path

算法：二分答案

给出一个 $n$ 行 $m$ 列的网格图，$0$ 到 $n \times m -1$ 的数在图上各出现一遍。需从 $(0,0)$ 出发，每次向下或向右行走并取出数字，求最后取出数字集合的 $mex$ 的最大值。

$mes$ 表示集合中出现的最小的非负整数。

可以记下每个数字的位置，对 $mex$ 进行二分答案，对于 $0$ 到 $mex-1$ 的数的位置，我们发现 $x,y$ 均需单调不降，排序判断即可。

3.xor

算法：线性基+拟阵+线段树

有一些护身符，每个数都有一个美观值 $w$ 和特征值 $c$，将护身符分为若干子集，如果子集的亦或和不为 $0$，便将子集美观值的和计入贡献。

每次会买出或卖出护身符，求每次操作后美观值和的最大值。

4.subgraph

算法：tarjan+并查集

给出 $N$ 个点 $M$ 条边的简单无向图，定义一个 $k$ 度子图 $G$ 为：

每个点的度数 $\ge k$
$G$ 连通
$G$ 极大

定义 $n$ 为 $G$ 的点数，$m$ 为边数，$g$ 为割的大小。再给出三个常数 $k1,k2,k3$，求出最大化 $m \times k1 - n \times k2 + g \times k3$ 时 $k$ 的值。

2023.08.14

1.up

算法：动态规划dp

给出一个二元函数 $f$ 和序列 $a$:

$f(x,n)=x~mod~a_n$
$f(x,i)=(x~mod~a_i)+f(x~mod~a_i,i+1)$

求 $x$ 取任意非负整数时，$f(x,1)$ 的最大值。

因为每次都会 $mod~a_i$，所以整个递归图是单调不升的，所以我们可以将图分为两部分，一部分为 $mod~a_i$ 后不变的部分 $x$，一部分为 $mod~a_i$ 后变化过的贡献 $y$：

于是我们可以用 $map$ 维护这样的二元组 $(x,y)$，然后我们考虑两种转移操作：

将 $x$ 直接对 $a_{i+1}$ 进行取模。
将 $x$ 缩进到 $a_{i+1}-1$。

即为：

\[ dp_{x~mod~a_i} \gets y+i \times (x-x~mod~a[i+1]) \]

\[ dp_{a_{i+1}-1} \gets y+i \times (\left \lfloor \frac{x+1}{a_{i+1}} \right \rfloor \times a_{i+1}-a_{i+1}) \]

最后就是求最大的 $n \times x+y$，枚举即可。

2.family

算法：线段树

给出一个 $2 \times n$ 的图，第一行的节点为 $1,2~...~n$，第二行的节点为 $n+1,n+2~...~2 \times n$，有的点不可去。

求 $Q$ 组点对的最短路，或是无法抵达。

对于 $n$ 列，维护线段树从最左到最右的$4$种情况的最短路，最后根据给出的 $u,v$ 对可行路径取 $min$ 即可。

3.love live

算法：状压+折半

有 $N$ 场演出，每场演出的价格为 $p_i$ 元，有 $M$ 元预算，求观看活动的方案数。

可以将 $N$ 折半，先将两组状压，再进行排序，最后对于两组进行二分合并即可。

4.izumi

算法：差分+亦或前缀和+容斥

有 $n$ 种漫画，书柜有 $m$ 列，每种漫画在 $(l_i,r_i)$ 列均有出现，定义一个区间所有已购买漫画的数量均为奇数时，该区间为满意的区间。

求满意区间的数量。

因为两个相同的数亦或会互相抵消，所以我们可以考虑用亦或维护奇偶条件。于是我们不想要一个区间的亦或和有值的时候计算贡献，而是为0时。所以我们可以将差分的区间 $(l_i,r_i)$ 右移得 $(l_i+1,r_i)$，这样合法的区间亦或和就会变为0，即：

对于一个合法区间 $(l,r)$，$sum_r=sum_l$，等价于亦或和为 $0$ 。

于是我们可以用 $map$ 来计算每个 $sum$ 的贡献，再减去空区间即可。

2023.08.16

1.de

算法：扫描线

给定序列三个长度为 $n$ 的序列 $a,b,c$ 。定义区间 $(l,r)$ 的价值为 $a_l,...a_r$ 按位与，$b_l,...,b_r$ 按位或，$c_l,...c_r$ 的最大公因数的乘积。

对于每次查询给出区间 $(l,r)$，求满足 $l\le l'\le r'\le r$ 的 $(l',r')$ 的价值之和。

首先可以发现按位与、按位或和 $gcd$ 每次的变化都是 $log$ 级别的，所以一定可以把这些答案分为 $log~n$ 个区间。

于是考虑扫描 $r$，对于每个 $i$ 维护 $l \le i$ 的答案之和 $sum_i$ ，这样答案才能用前缀和的形式表达出来，然后我们设：

$a_i'=a_i~and~...~a_r$
$b_i'=b_i~or~...~b_r$
$c_i'=gcd(c_i~...~c_r)$

我们考虑计算每次 $r$ 右移的贡献，可以发现当 $a_i'~,b_i'~,c_i'$ 在一次右移操作中未改变时，其变化量与上一次的变化量一致。又因为三者的变总数为 $log~n$ 级别，所以变化点可以暴力寻找。

接下来我们对于每个 $i$，只需要维护上一次被修改的变化量 $val_i$ 和上一次修改的时间 $t_i$，再记总时间为 $T$，于是转移为：

$sum_i=sum_i+val_i \times (T-t_i+1)$

最终复杂度即为 $O(n~log~n+m)$。

2.motive

算法：单调栈+前缀和+逆元

定义 $avg$ 为序列中一段区间的平均值， $exavg$ 为去掉最高和最低权值后的 $avg$。

对于一个序列 $a$ 我们定义它的 $k$ 号权值为：

\[avg \{exavg ~ A[l...r]|1\le l,r\le n,r-l\ge 2\}\mod k \]

现在给你一个正整数序列，需求它的 $k$ 号权值。

这道题我们考虑对于每个数将贡献拆开计算，即将总情况数减去 $a_i$ 作为最大值和最小值的情况数，可以用单调栈处理出每个 $a_i$ 为最小值的区间 $[lmin_i,rmin_i]$ 以及为最大值的区间 $[lmax_i,rmax_i]$。

于是我们定义 $f(l,r,p)$ 表示:

$f(l,r,p)=\sum\limits_{i=l}^p \sum\limits_{j=p}^r \frac{[j-i \ge 2]}{j-i-1}$

计算 $f(l,r,p)$ 时，需要枚举区间，时间复杂度难以支持，所以我们考虑进行容斥，再定义 $h(l,r)$ 为：

$h(l,r)=\sum\limits_{i=l}^r \sum\limits_{j=i}^r \frac{[j-i \ge 2]}{j-i-1}$

于是：

$f(l,r,p)=h(lr)-h(l,p)-h(r,p)$

我们再尝试化简 $h(l,r)$：

\[h(l,r)=\sum\limits_{i=l}^r \sum\limits_{j=i}^r \frac{[j-i \ge 2]}{j-i-1} \]

\[~~~~~~~~~=\sum\limits_{k=2}^{r-l}\frac{r-k-l+1}{k-1} \]

\[~~~=\sum\limits_{k=2}^{r-l}\frac{r-l}{k-1} -1 \]

\[~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~=(r-l)\sum\limits_{k=2}^{r-l}\frac{1}{k-1} -(r-l-1) \]

只需要预处理 $\frac{1}{k-1}$ 即可。

3.math

算法：数学

在 $x$ 轴的正半轴上，给定两个定点 $A, B$，以及正半轴上一点 $M$。求在射线 $OM$ 上一点 $P$ 使 $∠APB$ 达到最大值。

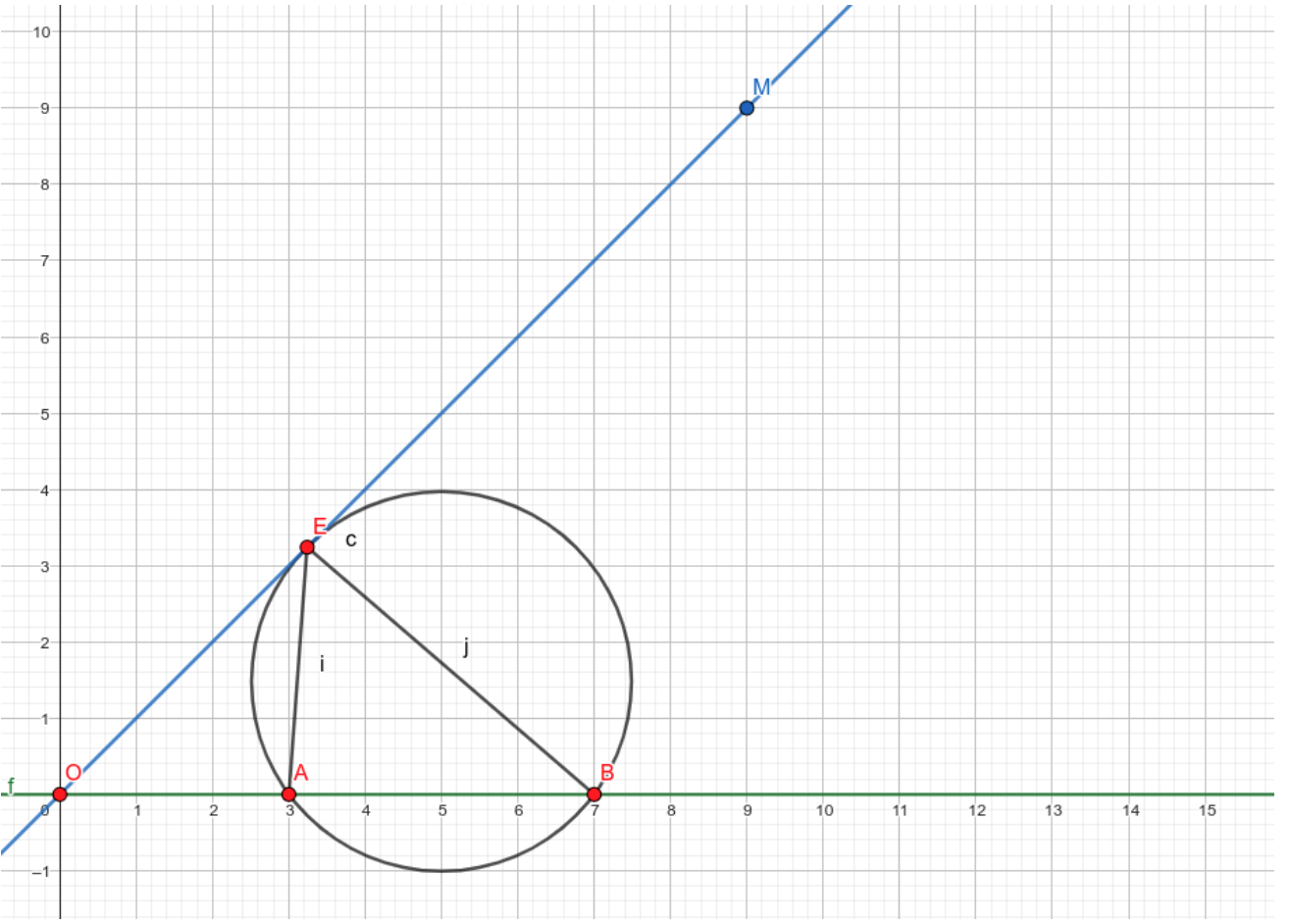
如上图，构造 $\odot~EAB$ 为点 $E,A,B$ 的外接圆且与 $OM$ 相切于点 $E$。此时 $\angle~AEB$ 最大。

求 $E$ 的坐标可以使用切割线定理或者相似三角形， $OE^2=OA \times OB$，再通过斜率计算 $E$ 坐标即可。

4.interval

算法：动态规划dp+贪心

给定 $n$ 个区间，第 $i$ 个区间是 $[a_i,b_i)$。需要把它们分成 $k$ 组，使得每个区间恰好被分在一组中，且每个组至少有一个区间，且同一个组中所有区间的交不为空。

需最大化每个组的区间的交的长度之和。

我们可以去除存在包含关系的区间，使得剩下的区间存在一个左右端点均单调的顺序。如果两个区间存在包含关系，那么大区间要么和小区间一组，要么单独一组。否则将大区间移到小区间那一组答案一定不会更劣。而大小区间一组时大区间不需要考虑。因此我们只需要排序之后做一个 $dp_{i,j}$, 表示前 $i$ 个小区间划分为 $j$ 组的最大贡献，大区间贪心即可。

2023.08.18

1.sequence

算法：树状数组

认为一个长度为 $l$ 的序列 ${a_1, . . . , a_l}$ 是好的，当且仅当这个序列满足如下条件：

不存在 $x, y, z$ 满足 $1 ≤ x < y < z ≤ l$ 且满足 $a_x < a_z < a_y$。
不存在 $x, y, z$ 满足 $1 ≤ x < y < z ≤ l$ 且满足 $a_y < a_z < a_x$。

求一个长度为 $n$ 的序列的 $2^n -1$ 个子序列中有多少个好的序列。

我们可以从 $a_z$ 的角度来分析，在 $a_z$ 左侧不能同时有大于和小于他的数。

直接枚举 $a_z$ 不方便统计答案，我们可以换一种思路：当我们确定第一个元素的时候，答案子序列则由以第一个元素开头的最长上升子序列和最长下降子序列组成，我们用树状数组来维护这两种序列即可。

2.puxi

算法：线段树

有一个 $n$ 行 $m$ 列的矩阵 $A$，初始所有元素都为 $0$。

每次执行三种操作中的一个：

$1 \ \ r_i$，即矩阵的第 $r_i$ 行全部赋值为 $i$。
$2 \ \ c_i$，即矩阵的第 $c_i$ 列全部赋值为 $i$。
$3\ \ r_{i,1} \ \ c_{i,1}\ \ r_{i,2}\ \ c_{i,2}\ \ k_i$，求从 $(r_{i,1}, c_{i,1})$ 到 $(r_{i,2}, c_{i,2})$ 的最短路，其中不经过 $a_{i,j} < k$ 的 $(i, j)$，不连通则输出 $-1$。

3.gnsi

算法：几何数学

给你三个正交矩形和一个点，问是否存在一个三角形，使得该三角形的三个顶点分别在三个正交矩形内，且该三角形的重心为给定点。

正交矩形：四条边都平行于坐标轴的矩形。

重心 $G=(\frac{x_A+x_B+x_C}{3},\frac{y_A+y_B+y_C}{3})$ ,只需满足下面两个条件

$x_G\in[\frac{minx_A+minx_B+minx_C}{3},\frac{maxx_A+maxx_B+maxx_C}{3}]$

$y_G\in[\frac{miny_A+miny_B+miny_C}{3},\frac{maxy_A+maxy_B+maxy_C}{3}]$

4.tree

算法：树形dp

给定一个 $n$ 个点，以 $1$ 为根的二叉树，每个点有两个权值 $a_i,b_i$，权值小于 $K$。

您可以执行两种操作：

选定 $x,y$，令 $a_x=(a_x+y)\mod K,b_x=(b_x+y)\mod K$。
选定 $x,y$，令 $x$ 子树內的点 $i$ 执行 $a_i= (a_i+y)\mod K$ 以及 $b_i=(b_i+y)\mod K$。

求让所有点满足 $a_i\ge b_i$ 的最小操作次数。

2023.08.19

1.sequence II

算法：数学

现在有一序列 $A$，里面有一个数 $x$。

设末尾的数是 $y$。你可以在 1 到 $\lfloor\sqrt y\rfloor$ 中选取一个数 $z$ 加到序列的末尾。

进行若干次，问一共有多少种可能的情况。

首先对于 $x \le 10^{12}$ 有 $O(\sqrt{x})$ 的做法：

\[\sum\limits_{i=\sqrt{x}}^{1} sum_{i} \to sum_{i-1} ~| ~sum_i\to sum_{\sqrt{i}} \]

但对于 $x \le 10^{18}$ 时，我们需要将每个开根以后为 $k$ 的数各分作一个区块，我们发现 $k^2$ 与 $(k+1)^2$ 之间只存在 $2 \times k$ 个数，于是我们得到了新的转移：

\[\sum\limits_{i=\sqrt[4]{x}-1}^{1} sum_{i}+2 \times (i-1) \to sum_{i-1} ~| ~sum_i\to sum_{\sqrt{i}} \]

注意 $\sqrt[4]{x}$ 的情况不一定有 $2 \times \sqrt[4]{x}$ 个数，需要分开计算，时间复杂度即为 $O(\sqrt[4]{x})$。

2.math II

算法：数学

给定 $n$, 求出满足 $x \times y+1 | x^2+y^2(1 \le x \le y \le n)$ 的 $(x,y)$的对数。

需回答 $t$ 次询问。

对于条件我们可以写成下面的式子：

$x^2-kxy+y^2-k=0$

通过韦达定理可以得出两组解的关系：

$x_1+x_2=ky$

对于原式，可以构造一组 $y=x^3,k=x^2$ 的解，于是我们通过这一组解来扩展，即 $x_2=ky-x_1$，因为扩展的速度极快，数量级约为 $O(n ^{\frac{1}{3}}~log~n)$。

3.doog

算法：矩阵构造+线段树

定义一个序列 $A$ 是好的，当且仅当每次选取两个相邻且相同的数删除，可全部删完。

接下来完成 $q$ 次操作：$(0 \le a_i \le 2)$

给定 $l, r$，需要对于 $l ≤ i ≤ r$，把 $a_i$ 变为 $(a_i + 1) \mod 3$。
给定 $l, r$，判断 $\{a_l . . . a_r\}$ 是否是好的序列。

4.trolcon

算法：动态规划dp

你有 $n$ 个区间，第 $i$ 个区间可以表示为 $[l_i , r_i ]$。

定义一个区间编号的集合 $S$ 为可支配的，当且仅当对于所有区间 $i$，都至少满足以下两个条件之一：

$i ∈ S$。
存在 $k ∈ S$，$[l_i , r_i]$ 与 $[l_k, r_k]$ 相交。

求至少需要进行多少次合并操作，使区间集合的最小可支配集合大小至少 $-1$。

2023.08.22

1.hard

算法：数学

给定正整数 $p,k$ ，问有多少种方案可以构造出一个长度为 $p$ 的序列，对于一个 $x(0 \le x < p)$ 满足：

$f_{kx \% p}=k\times f_x \% p$

可以发现，这种等式构成了若干个循环，而每一种循环又有 $p$ 种可能，所以最后答案即为 $p$ 的环的个数的次方，暴力找每个环即可，同时也要注意 $k=0/1$的特判。

2.extreme

算法：动态规划dp

给出一个序列 $a$，我们定义一个区间的极端值为下列操作的最小次数：

将 $a_i$ 分解成 $x,y(x+y=a_i)$，直至区间成为不降序列。

求序列 $a$ 所有区间的极端值的和。

我们对于每个右端点，从右往左计算，当我们目前的不降序列的最小值为 $x$ 时，我们需要分解一个 $a_i$。可以发现，如果 $a_i > x$ 就需要把 $a_i$ 平均分解为 $\left \lceil \frac{a_i}{x} \right \rceil $ 份，分解完后的最小值即为 $\left \lfloor \frac{a_i}{\left \lceil \frac{a_i}{x} \right \rceil } \right \rfloor $。如果直接像这样暴力贪心，时间复杂度为 $O(n^2)$，对于 $n \le 10^5$ 的量级显然不行。

通过观察发现，$a_i \le 10^5$，我们可以根据值域构造状态 $dp_{i,j}$ 表示选到第 $i$ 个数时值为 $j$，我们发现 $a_i$ 整除 $[l, r]$ 内所有数向上取整的结果相同，可以通过向上取整的数论分块实现，于是我们设 $v$ 为 $a_i$ 分裂后的最小值，转移即为：

\[\sum\limits_{i=l}^{r}dp_{i+1,j} \to dp_{i,v} \]

最终的时间复杂度为 $O(n \sqrt{a_{i}})$。

3.fraud

算法：矩阵构造+线段树

给定 $n$ 个麻将，正面和反面有 $A,B$ 和未知三种状态，我们定义 $n$ 个麻将重在一起时，接触的两面各不相同即为成功。

求对于所有未知状态的所有情况成功的概率。

容易构造出两种合法情况：

$AB,AB,AB...AB$
$BA,BA,BA...BA$

当这两种情况结合起来时，我们便需要 $AA$ 和 $BB$ 连接，我们可以分类讨论，再对只有 $AA,BB$ 的情况进行特判即可。

4.easy

算法：动态规划dp

给定一个长度为 $n$ 的排列 $p$，进行 $m$ 次以下操作:

每次选定区间 $[l,r]$ 进行反转。

计算所有 $({\frac{n \times (n+1)}{2}})^m$ 中 $\sum\limits_{i<j}[p_i>p_j](j-i)$ 的和。

首先对于 $(j-i)$ 明显不好计算，于是我们将其拆开计算：

\[\sum_{i<j,p_i>p_j}j-\sum_{i<j,p_i>p_j}i\text{。} \]

再以 $i$ 或 $j$ 的角度再次化简：

\[\begin{aligned}&\sum\limits_{i=1}^ni\sum\limits_{j=i}^{i-1}[p_i<p_j]-\sum\limits_{i=1}^ni\sum\limits_{j=i+1}^n[p_i>p_j]\\ = & \sum\limits_{i=1}^ni\left(\sum\limits_{j=1}^{i-1}[p_i<p_j]-\sum\limits_{j=i+1}^n[p_i>p_j]\right)\end{aligned} \]

因为计算的条件并不统一，所有我们考虑旋转后再次计算：

\[\begin{aligned}& \sum\limits_{i=1}^ni\left(\sum\limits_{j=1}^{i-1}[p_i<p_j]-\sum\limits_{j=i+1}^n[p_i>p_j]\right)\\=& \sum\limits_{i=1}^ni\left(\sum\limits_{j=1}^i[p_i<p_j]-\sum\limits_{j=i+1}^n[p_i\ge p_j]\right)\\= & \sum\limits_{i=1}^ni\left(\left(i-\sum\limits_{j=1}^i[p_i>p_j]\right)-\sum\limits_{j=i+1}^n[p_i>p_j]\right)\\= &\sum\limits_{i=1}^ni\left(i-\sum\limits_{j=1}^n[p_i>p_j]\right)\end{aligned} \]

我们再借助排列这个优秀的性质推出：

\[\begin{aligned} &\sum\limits_{i<j,p_i>p_j}(j-i)\\=& \sum\limits_{i=1}^ni(i-p_i)\\=& \sum\limits_{i=1}^ni^2-p_i\times i\end{aligned} \]

但因为有 $m$ 次反转操作，直接计算 $p_i \times i$ 显然不可行，所以我们就只需要求出初始在位置 $i$ 的元素操作 $m$ 次后到达的位置的期望 $s_i$
，答案即为：

\[\binom{n+1}2^m\sum_{i=1}^ni^2-s_i\times p_i \]

我们对于一个点 $i$ 旋转到 $j$ 的方案数为 $min(i,n-i+1,j,n-j+1)$，我们发现把 $i$ 反转到 $j$ 和 $n-j+1$ 的方案数是一样，所有对于每个点反转后的期望位置均为 $\frac{n+1}{2}$，于是得到:

\[s_i=q \times i + (1-q) \times \frac{n+1}{2} \]

总时间复杂度为 $O(n~log~m)$。

2023.08.23

1.statement

算法：数位dp

对一个数进行操作把这个数字各个数位上的数按照不降序进行排列，之后把所有的前导零去掉。
再对 $[L,R]$ 里的数都进行操作，最后能得到多少不同的数。

这道题一眼数位dp，但发现像普通数位dp一样进行类似 $s_r-s_{l-1}$ 的前缀和操作并不方便。可以发现，排序后去除前导零的数的种类，在 $10^{18}$ 量级中在 $5 \times 10^6$ 以内，所以我们考虑枚举每一种情况来判断是否能在 $[l,r]$ 范围内。

我们可以枚举每种数字的个数，再运用数位 $dp$ 进行判断：

设计状态 $dp_{pos,lim1,lim2}$，表示当前处理到第 $pos$ 位，是否顶到上界或触碰下界，对于每次选择的数字，在原先选择的数字个数中减一即可。

2.nothing

算法：多重背包

给定正整数 $n,k,M$，且 $M$ 为质数。对于 $x=1,2,...,n$，求有多少个非空的可重集满足：

可重集中的元素均为 $[1,n]$ 中的正整数。
可重集中相同元素的数量不超过 $k$。
可重集中元素的平均数为 $x$。

对于每个 $x$，平均数显然不好处理，这里我们转换一个思路：

将 $x$ 变为 $0$，这时我们需要选的数的值域也从 $[1,n]$ 变为了 $[1-x,n-x]$。显然，对于值域中的 $0$ 可以选 $0-k$ 个，再要求其他数的和也为 $0$ 即可。

转换后，我们相当于在 $[1-x,-1]$，$[0,0]$ 和 $[1,n-x]$ 三个区间拿东西，我们定义 $dp_{i,j}$ 为前 $i$ 个数的和为 $j$ 的方案数，答案即为：

\[(k+1)\times\sum_{j=1}^{\textit{sum}} f _ { i - 1 , j }\times f_{n-i,j}-1 \]

其中 $sum$ 表示能取到的最大值，还可以用前缀和优化此 $dp$，时间复杂度 $O(n^2k)$。

3.short

算法：字符串

对于字符串 $s$，定义 $f(s)$ 为 $s+rev(s)$，其中 $rev(s)$ 表示 $s$ 的反串。

给定字符串 $t$。求出最短的字符串 $s$，使得 $s$ 经过若干次 $s\rightarrow f(s)$ 后 $s$ 能够变成 $t$。

可以每次暴力判断是否可以折叠即可，时间复杂度为 $O(n+\frac{n}{2}+\frac{n}{4}...)$，即 $O(n)$。

4.set

算法：图论

对于无向图 $G(V,E)$，我们称点集 $A\in V$ 是独立集,当且仅当对于任意 $i,j\in A$，点 $i,j$ 在 $G$ 中无边相连。称点集 $A\in V$ 是支配集，当且仅当每个 $V-A$ 中的点都和至少一个 $A$ 中的点有边。这里，$V-A$ 表示集合 $V$ 和集合 $A$ 的差集，称集合 $A$ 是独立支配集，当且仅当 $A$ 同时为独立集和支配集。

对于大小为 $n$ 的点集 $V_0$，编号为 $i$ 的点带点权 $p_i$，其中 $p$ 构成一个 $1\sim n$ 的排列。接下来，按照如下方式构造 $E_0$：对于任意两点 $i<j$，如果 $p_i>p_j$，则向 $E_0$中加入一条连接 $i,j$ 的无向边。

现在，给定 $G(V_0,E_0)$，请求出 $G$ 的独立支配集数量，答案对 $998244353$ 取模。

这道题我们可以先将原序列 $p$ 还原，再来分析两种情况：

独立集：在序列上的上升序列。
支配级：序列的最大值和最小值包含序列外所有数。

于是问题就很简单了，我们只需要维护 $dp_i$ 表示序列从 $1-i$ 极大单调递增子序列的数量即可。

2023.09.24

1.kel

算法：贪心

给定 $n,L,R$，需要构造出长度为 $n$ 的序列满 $a$ 足：

值域在 $[L,R]$ 。
保证所以不相交的子序列不相同。

要求字典序最小，无解输出 $Shinomiya$ 。

我们发现当 $a_{i...j}$ 和 $a_{k...l}$ 相同时，他们前两位一定是相同的，即为 $a_{i,i+1}=a_{k,k+1}$，所以我们只需要考虑长度为 $2$ 的不相交子序列不同即可。当我们不限定值域时，可以简单构造出一种方案：

\[\begin{aligned} (0,0),(0,1),(0,2),(0,3),(0,4)...\end{aligned} \]

所以我们结合值域即为：

\[\begin{aligned}(l,l),(l,l+1),(l,l+2)...(l,r)...\end{aligned} \]

这里需要注意一个细节，我们每个交节处都是 $(r,l+1),(r,l+2)...$，其中还没有出现 $(r,l)$，所以我们还需要在结尾加上 $(r,l)$，而且结尾可以有三个 $r$，所以我们的结尾形式即为 $rrrl$，最后实际的上界即为：

\[\begin{aligned}n > (r-l+1) \times (r-l+2)+1\end{aligned} \]

2.gen

算法：位运算+图论

定义 $f(x,y)=(x \oplus y) \times (x ~\&~ y) \times (x ~|~ y)$，给出一个 $n$ 个点 $m$ 条边的无向无环图，可能有重边，设 $deg_i$ 为点 $i$ 的度数，求 $\sum\limits_{i=1}^{n} \sum\limits_{j=1}^{n} f(deg_{i},deg_{j})$。

有位运算初步想到按位讨论，但乘法并不好处理，于是可以思考无向图度数的性质，我们发现每增加一条边就有两个点的度数同时增加，
易得：$\sum\limits_{i=1}^{n} deg_{i}=2m$ ，然后我们发现本质不同的 $deg$ 实际上只有 $\sqrt m$ 的量级，所以我们直接离散化计算每种值的贡献，时间复杂度为 $O(m+n)$ 。

3.fight

算法：树形dp

给定一个长度为 $n-1(n=2^k)$ 的序列 $a$ 和一个数字 $x$，将 $x$ 放进序列的每一个位置，并进行以下操作直到剩下一个数：

将序列前两个数 $a_1,a_2$ 拿出进行决斗，其中 $a_1$ 获胜的概率为 $\frac{a_1}{a_1+a_2} $，$a_2$ 获胜的概率为 $\frac{a_2}{a_1+a_2} $，将赢的数放到末尾，输的数出列。

求每个位置的 $x$ 留到最后的概率。

因为每次选择两个数决斗，并且 $n=2^k$，所以我们可以建一棵二叉树来记录决斗胜负的状态，然后考虑树形 $dp$。首先可以设 $dp_{i,j}$ 为点 $j$ 在子树 $i$ 中留下的概率，需要 $O(n^2)$ 求出概率，再枚举 $x$ 的位置，时间复杂度来到 $O(n^3)$，显然不可行。

我们发现每次 $dp$ 是求出了所有点的概率，我们只需要求 $x$ 的概率，所以只需要从 $x$ 点一直向上计算，求出中途经过的子树和点的概率即可，这样每次计算 $x$ 的概率就缩小成了 $O(n)$，枚举位置后的 $O(n^2)$ 可以接受。

4.act

算法：博弈论

给出两个数 $a,b$，和两个序列 $A,B$，由 $Alice$ 和 $Bob$ 轮流操作，每次可以将 $a$ 或 $b$ 减去一个不大于自身的正整数，直到：

$a=0 ~\&~ b=0$
$a=A_i ~\&~ b=B_i$

求 $Alice$ 先手的胜负情况。

2023.09.26

1.mountain

算法：单调栈

给出一个高度序列 $h$，我们定义一座山 $i$ 能看到另一座山 $j$ 当且仅当 $\sum\limits_{k=i}^{k \le j} h_k \le h_i$，求在每座山上能看到几座山。

我们用单调栈维护每座山的左端第一个比它高的和右端第一个比它高的，每座山的答案即为: $(maxr_i-1)-(maxl_i+1)$。

2.game

算法：博弈论

给出一个长度为 $n$ 的 $01$ 串，$C$ 和 $D$ 轮流操作，每次可以将一段长为 $k$ 的连续子段全变为 $0$ 或 $1$，操作后 $01$ 串全为同一字符的一方获胜。

问当 $C$ 先手时 $C$ 的胜负情况，平局输出 $tie$。

我们发现，当先手的 $C$ 进行操作后，如果不能直接获胜，那么他以后都不能获胜了，变为了不胜态，因为 $D$ 不会再给 $C$ 胜点。所以如果 $C$ 获胜只有第一次操作有机会，我们先处理出最左端和最右端的 $01$，一次操作制胜即为所有的 $1$或$0$ 都包含在一个连续 $k$ 子段中，于是我们容易得到 $min(r1-l1+1,r0-l0+1) \le k$ 满足时一方可以制胜，除非两人彼此都不给对方胜点。

所以我们推断出 $win$ 的情况只需要第一次操作判断一下，那么 $lose$ 和 $tie$ 的情况该如何讨论。一个很明显的思路，我们可以枚举 $C$ 操作后每一次的局面是否全部都可以被 $D$ 制胜，即 $lose$ 的情况，但时间复杂度来到了 $O(n^2)$，无法接受。我们考虑如果 $C$ 无法一次制胜时，他的操作在 $n \le 2 \times k$ 时一定会改变 $01$ 的最左和最右端点的位置，所以我们只需要判断是否 $min(r1-l1+1,r0-l0+1) \le k-1$ 即可，另外的情况两人将为相互纠缠，即为平局情况。

3.imp

算法：扫描线

给出 $n$ 个坐标为 $(x_i,y_i)$，权值为 $c_i$ 的点。在 $y=x$ 上找两点作为左下角和右上角的点作一个正方形，求点权之和减去正方形边长的最大值。

可以容易的想到，一定有点会在正方形的边界上，于是我们发现，一个点 $(x,y)$ 能被包含到的最小正方形为 $(min(x,y),max(x,y))$。问题转换成了：有 $n$ 和带权值的区间 $(x_i,y_i)$，求选取一个大区间并最大化大区间包含的区间权值和减去大区间长度的差。

我们可以将区间集先离散化，再计算每个三元组 $(x,y,c)$ 对答案的影响：可以在每个 $l$ 点插入 $(r,c)$，从右往左扫描，当扫到点 $i$ 发现有 $(r,c)$ 被插入时，对于 $(r,n)$ 的答案增加 $c$ 的贡献，区改区查线段树维护即可。

4.tree

算法：线段树

给出一个 $n$ 个点的树和 $k$，求出树上剩下 $[l,r]$ 点时连通块的数量 $f^k(l,r)$ 的和。

我们首先需要发现一个规律：

连通块数量=点数-边数

我们发现，对于树上每一个点 $(u,v)$，可以看作一个影响区间，对于所有包含这个区间的大区间，边数都会 $+1$ 对应的连通块数量也会 $-1$。于是我们直接从左往右枚举右端点，维护所有左端点的答案。

可以在 $max(u,v)$ 处插入 $min(u,v)$，当我们右端点到达 $max(u,v)$ 时，对于 $(1,u)$ 区间的答案会 $-1$，最后用线段树维护区间和以及平方和即可。

2023.09.27

1.path

算法：动态规划dp

有 $n$ 个史莱姆排成一列，每个史莱姆有 $a_i$ 战力，我们有一把武器功击力为 $P$。我们称每次浪费的战力为 $P-a_i(P \ge a_i)$，我们可以改变 $k+1$ 次武器的攻击力。

求打败所有史莱姆后浪费的最少战力。

我们可以发现每次武器的攻击力 $P$ 都会攻击到一个区间，所以我们考虑区间 $dp$，设 $dp_{i,j}$ 表示打败 $[1,i]$ 的史莱姆并且改变了 $j$ 次攻击力浪费的最少战力，转移即为：

\[\begin{aligned}dp_{i,j}=min(dp_{k,j-1}+max(a_{k+1},a_{k+2}...a_i)\times(i-k)-(sum_i-sum_k))\end{aligned} \]

2.gaze

算法：线段树+离散化

给出一个 $n$ 个点的链，链上每个点有一个点权，每次有两种操作:

把点 $a$ 的点权改为 $b$。
给出一个 $x$，求删除所有点权小于 $x$ 的点及其边后的连通块数量。

对于一条链的连通块，我们可以找每个连通块的第一个数，即下标为 $i$ 且满足 $a_{i-1} < x \le a_i$ 的数，反推过来，相当于给 $a_{i-1}$ 和 $a_i$ 中间的所以询问的 $x$ 都有 $1$ 的贡献。

所以我们将所有询问的数进行离散化，再对于所有 $a_i>a_{i-1}$ 在离散化后的询问中二分找到能提供贡献的区间。至于修改点权，只会影响到相邻的两个数，删掉先前点权的贡献，再加上新点权贡献即可。

3.envelope

算法：差分约束+树形dp+线段树合并

4.crazy

算法：网络流

2023.09.28

1.trade

算法：动态规划dp

给出一个 $n$ 个点 $m$ 条边的有向有点权图，我们定义每走一条边需要一天，天数为 $T$，最大化起点和终点都为 $1$ 的路径的点权之和减去 $T^2$ 的差。

因为 $(T+1)^2-T^2=2T+1$，而我们观察到点权的值域只 $\le 1000$，所有我们断定 $T$ 最多只能走 $1000$ 天，否则答案只会负增长。

我们根据有向图建反边，枚举天数和点，定义 $dp_{i,j}$ 表示在第 $j$ 天到 $i$ 点的最大点权，根据反边转移即可。

2.graph

算法：二维偏序

给出 $n$ 个点，每个点有一个二元组 $(x_i,y_i)$ 作为点权。当 $x_i \le x_j \&\& y_i \le y_j$ 时，对于两个点 $i,j$ 连边，问连边后的连通块数量。

容易发现，对于一个 $x$ 坐标相同的点集一定能成为一个连通块，于是我们是需要保留每个 $x$ 坐标的集合最小和最大的 $y$ 值，离散化后按 $x$ 的升序依次进入优先队列，用最大的 $y$ 去连边即可。

3.milky

算法：动态规划dp

给出一个字符串 $s$，由 $m,i,l,k,y$ 组成，给出 $q$ 组 $(l,r)$，求存在多少组 $l \le a < b < c < d < e \le r$ 满足 $abcde=milky$。

我们可以记 $dp_{i,l,r}$ 表示现在匹配到了第 $i$ 位,匹配上了编号为 $l$ 到 $r$ 的字符的方案数，首先对于字符串 $s$ 进行初步处理：

   for(int i=1;i<=n;i++){
        for(int j=0;j<a[i];j++)
            f[i][j][a[i]]+=f[i-1][j][a[i]-1];
            
        for(int j=0;j<5;j++)
            for(int k=0;k<5;k++)
            	f[i][j][k]+=f[i-1][j][k];
                
        f[i][a[i]][a[i]]++;
    }

然后对于答案的统计我们需要容斥处理，定义状态 $solve(l,r,L,R)$ 表示在区间 $(l,r)$ 中的字符编号在 $(L,R)$ 之间的数量，我们可以先统计 $dp_{r,L,R}-dp_{l-1,L,R}$ ，最后还需要减去左端点在 $(1,l-1)$ 和右端点在 $(l+1,r-1)$ 的所有区间即可。

4.easiest

算法：倍增

2023.09.30

1.gather

算法：树状数组

给出一个序列 $a$，求有多少组 $(l,r)$ 满足：区间端点上的数不等于区间内的其他数。

我们可以枚举右端点，当我们发现当前右端点 $r$ 之前有一点 $l'$ 与 $r$ 相同时，可以推测出 $r$ 之后的所有 $r'$ 都不能以 $l'$ 为左端点，于是我们在树状数组上做上标记，依次计算每个 $r$ 有多少个合法的左端点最后求和。

2.greedy

算法：动态规划dp

3.number

算法：AC自动机+动态规划dp

4.geometry

算法：计算几何

一条平行于等边三角形底边的射线从距离底边左端点 $l$ 的腰上的点处进入，问在边长为 $L$ 的等边三角形中反射直到回到入射点经过的长度。

容易发现反射的前两条边总和为 $L$，这两条边分开讨论，而之后的反射边每次长度为 $L \% (L-l)$，总共出现了 $L / (L-l)$ 次，类似于辗转相除，直接计算即可。

2023.10.01

1.device

算法：枚举

给出一个不含 $0$ 的三位数 $k$，将 $k$ 放入一个队列中并进行 $n$ 次操作:

将队列中每个数拿出并乘上 $1001$，再从所得六位数中任意选取三个数字组成新的三位数，最后将组成的三位数放入原序列。

求最后序列中三位数的种类数。

容易发现每次乘 $1001$ 的操作相当于将原三位数进行了一次复制，所以对于原三位数的每个数字也会进行一次复制操作，而三位数最多可以容纳三个数字，直接讨论 $n\in(0,1,2)$ 的情况即可。

2.triple

算法：枚举+搜索

3.badge

算法：根号分块+扫描线

4.grid

算法：莫比乌斯反演

2023.10.02

1.casio

算法：线性筛

给出一个 $n$ 和 $p$，求不小于 $n$ 的最小的质数或最小质因子大于 $p$ 的数。

我们可以直接线性筛，处理出所有质数的同时，给所有最小质因子大于 $p$ 的数打上标记。因为在 $\le 3e7$ 的质数中，两两间隔最大为 $200$，分布较为均匀，所以我们可以直接从 $n$ 往后暴力判断，其中注意一个线性筛的优化：

当 $i \% prime[j]$ 时直接 $break$可以保证每个数只被筛一遍。

~~考场没加优化也能过~~。

2.car

算法：贪心+动态规划dp

3.cexcellent

算法：字符串

给出一个字符串 $s$，问在其所有子串中有多少种方法能拆成 $AABB$ 的形式，两种方法不同当且仅当 $|A|$ 或 $|B|$ 不同。

我们可以枚举分割点，即分割 $AA$ 和 $BB$ 的点，然后可以枚举左端点的可行情况数，右端点的可行情况数，利用乘法原理计算贡献即可。但直接枚举分割点 $O(n)$，计算左右端点情况数 $O(n^2)$，总时间复杂度来到了 $O(n^3)$，显然不可行。

因为枚举分割点和左右端点无法省去，所以我们预处理一个 $f_{i,j}$ 表示两个初始点为 $i$ 和 $j$ 的相同的串的长度，我们只需要判断 $AA$ 和 $BB$ 的两串的 $f_{start1,start2}$ 是否能覆盖整个 $A$ 或 $B$ 即可。

4.robot

算法：拓扑排序+线段树优化建图

2023.10.03

1.jump

算法：单调栈

给出一个小标从 $1$ 开始的序列 $a$，并定义 $a_0=\infty $，对于一个下标为 $x$ 的点，我们可以跳到 $y$ 当且仅当 $y<x \&\& a_y>a_x$，求从每个点开始的最大跳跃次数。

根据题意发现对于每个点能跳跃的最大次数其实就是从当前点往前的最长上升子序列，单调栈统计答案即可。

2.lca

算法：换根dp+LCA

给出一棵 $n$ 个点的树，求以每个点为根时的：

\[\begin{aligned}\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n}lca(i,j)\end{aligned} \]

我们可以先考虑当根为 $1$ 时点 $x$ 为两点的公共祖先时贡献该如何计算，发现两点的条件即为不在的同一子树上但在 $x$ 为根的子树上的点对，即：

\[\begin{aligned}res_x=siz_x^2-\sum\limits_{y \in son_x} siz_y^2\end{aligned} \]

然后我们发现对于每一个点不同根的贡献，只与它根所在的子树相关（此处定义除 $x$ 为根的子树以外的树也为 $x$ 的一个子树，根节点 $1$ 除外）。我们可以枚举根节点所在的子树，对公式进行预处理，最后直接在树上差分扩散子树贡献统计答案就解决了。

3.flip

算法：组合数学

4.explorer

算法：树状数组+二位偏序

2023.10.04

1.magic

算法：最小生成树

给出 $n$ 个四元组 $a,b,c,d$，其中数字 $[1,2 \times n]$ 各出现两次，我们定义每组的 $a$ 和 $b$ 以及 $c$ 和 $d$ 两两连边，每组相同数字也连边。我们可以改变第 $i$ 个四元组的顺序，代价是 $c_i$，求使每个元素组成一个环的最小代价。

我们尝试转换一下问题的模型，发现用 $c_i$ 的代价改变四元组的顺序，即为让 $b,c$ 连一条边。因为每个数的出度和入度一定为一，所以初始情况会形成若干个环，问题可以转换为：

可以用 $c_i$ 的代价将两个环合并，问全部环合并的最小代价。如果我们再把每个环看成点，即为有 $2n$ 个点和一些初始边，加一条 $b \to c$ 边的代价为 $c_i$，最小生成树即可解决问题。

2.cat

算法：动态规划dp

给出一个 $n \times n$ 的字符矩阵 $d \in \{L,R,U,D\}$，以及权值矩阵 $a$。我们定义两个格子 $(i_1,j_1)~(i_2,j_2)$ 能匹配成一对当且仅当:

$i_1=i_2,j_1<j_2,d_{i_1,j_1}=R,d_{i_2,j_2}=L$
$i_1<i_2,j_1=j_2,d_{i_1,j_1}=D,d_{i_2,j_2}=U$

一组匹配有若干对匹配组成，每组匹配的每个格子至多与一个格子进行匹配，一组匹配的权值定义为每对匹配的权值之和，求每组匹配的权值之和。

因为两种成对的条件互不影响，所以很显然可以分开讨论，首先讨论 $LR$ 的情况：

我们定义 $f_{i,j}$ 和 $g_{i,j}$ 表示在第 $k$ 行前 $i$ 列格子还有 $j$ 个 $R$ 没有匹配的方案数和权值和，那么转移将分为三种情况讨论：

$d_{i,j}\notin \{L,R\}:\begin{cases} f_{i,j}=f_{i-1,j}\\g_{i,j}=g_{i-1,j} \end{cases}$
$d_{i,j}\in {L}:\begin{cases}
f_{i,j}=f_{i,j}+f_{i-1,j+1}\times(j+1)\ g_{i,j}=g_{i,j}+g_{i-1,j+1}\times(j+1)+f_{i-1,j+1}\times(j+1)\times a_{k,i}
\end{cases} $
$d_{i,j}\in {R}:\begin{cases}
f_{i,j}=f_{i,j}+f_{i-1,j-1}\ g_{i,j}=g_{i,j}+g_{i-1,j-1}+f_{i-1,j-1}\times a_{k,i}
\end{cases} $

$d_{i,j} \in \{U,D\}$ 的情况修改一下 $dp$ 的判定即可，在处理完了所有方案数和价值和以后，因为每一行和每一列是分开的，所以我们会得到 $2 \times n$ 组互不影响的方案数和权值数，我们又将每一行和每一列看作一个个集体，问题可以简化为：

有 $2 \times n$ 个点，每个变化之点有一个情况数 $f$ 和权值 $g$，于是我们对于一个点 $i$ 统计答案即为将它自己的权值乘上它出现的次数，即为：

\[\begin{aligned}g_i\times(\prod_{j=1\&\&j\ne i}^{2\times n}f_j~)\end{aligned} \]

统计这个答案并不难，我们将所有 $f$ 处理一个前缀积和后缀积 $pre1$ 和 $pre2$，那么对于每个 $i$，答案统计就化简成了：

\[\begin{aligned}g_i\times pre1_{i-1}\times pre2_{i+1}\end{aligned} \]

总时间复杂度 $O(n^3)$。

3.random

算法：图论+环

给出一个 $n$ 个点 $m$ 条边的有向图，定义每两点之间都有一条有向边，除确定的有向边点对以外的有向边点对方向会随机生成。我们定义存在一个三元环为以下情况：

$(a,b,c)$ 三点存在 $(a \to b) , (b \to c) , (c \to a)$
$(a,b,c)(b,c,a)(c,a,b)$ 算作同一种情况，但 $(a,b,c)(c,b,a)$ 不算同种情况。

直接计算贡献我们不得不枚举三个点或三条边，时间复杂度至少在 $O(n^3)$ 量级，所以可以考虑切换思路——容斥。因为有 $n$ 个点，每个三元环需要三个点，所以总三元环数即为 $C(n,3)$，接着我们再考虑非法的情况。显然，在三个点中，任意一个点的入度或出度为 $2$ 时是非法的，但只需要讨论入度或出度其中一个即可。

于是我们考虑只讨论出度为 $2$ 时的非法情况，即同时存在 $(a \to b)(a \to c)$ 两条边，分类讨论比较简单，我们只有两种可能的边，即已知边和随机边，于是这两条边只有三种情况：$2$ 随机，$2$ 已知，$1$ 随机 $1$ 已知。直接枚举计算，因为：

随机边=(总点数-入度-出度-1)，已知边=出度。

4.chessboard

算法：字符串

给出一个 $n$ 行 $m$ 列的 $01$ 矩阵，其中含有一些未知位置，用问号表示，问是否存在一种方案使整个 $01$ 矩阵不出现以下两种矩阵：

\[\begin{aligned}\begin{bmatrix} 0&1 \\ 1 &0 \end{bmatrix} ~~or~~ \begin{bmatrix} 1&0 \\ 0 &1 \end{bmatrix}\end{aligned} \]

如果存在，输出 $Yes$ 并输出可行的矩阵，否则输出 $No$。

一个明显的思路，一些目前未知的点实际上是已知的，所以可以先将目前未知的点分成两组，已知的和未知的，我们可以直接将已知的点填入矩阵当中，但填入以后又会对矩阵造成什么影响？

考虑到非法的矩阵规格为 $2 \times 2$，所以对于一个点，只会影响到周围的 $4$ 个矩阵，即点任意一个点的改变，影响了左上、左下、右上和右下四个矩阵，我们判定这些被影响的矩阵内是否有目前的未知点，再判定填入数字以后目前的未知点是否会受到影响并变成已知点。

而排除所有已知点之后，可能仍有一些未知点，但他们有一个共同的性质：

不会受到周围矩阵的约束

显而易见这些点到最后可以随便填，因为不受周围矩阵的约束，它的值同样不会约束周围的矩阵，到这里问题就顺利解决了。

2023.10.05

1.travel

算法：亦或前缀和+图论

有一个数列 $a$，满足 $m$ 个区间 $(l_i,r_i)$ 的亦或和为 $s_i$，且值域 $0 \le a_i < 2^k$，求数列的种数，两种数列不同，当且仅当存在 $a_i \ne a'_i$。

考虑如果我们知道数列 $a$，那么 $m$ 个区间相当于在 $a$ 的抑或前缀和数组中限制 $sum_r \oplus sum_{l-1}=s_i$，因为确定了抑或前缀和数组之后相当于确定了数列 $a$，所以我们直接计算前缀亦或和数组的种数。

可以将 $m$ 个区间转换为边，让 $sum_r$ 和 $sum_{l-1}$ 连边从而产生关系，即确定其中一个另一个也会确定。再在建好的图上计算连通块的数量 $cnt$ ，答案即为 $(2^k)^{cnt-1}$。

2.reinforce

算法：状压dp

有一个由 $26$ 个字母随机排列而成的字符串 $T$，给出将 $T$ 复制 $cnt$ 次后的子序列 $S$，最小化 $cnt$。

一个暴力思路：可以直接枚举 $T$ 全排列的所有情况，在 $S$ 中跑一遍，我们设 $S$ 中出现了 $k$ 种字母，那么时间复杂度为 $O(|S| \times 2^k)$，对于 $k=20$ 的情况显然不可行。

我们观察到，当在一个排列中，后一个字母的字典序小于前一个字母时，他们一定不在同一个排列当中，于是我们考虑枚举每个字母的字典序。

我们设 $dp_{i}(i<2^k)$ 表示有哪些字母已经出现，先预处理 $S$ 中相邻的字母对，每次加入一个字母，再枚举已经加入的字母进行答案的统计，最后答案即为 $dp[2^k-1]$。

3.graph

算法：圆方树+树剖

4.permutation

算法：矩阵变换+数学

2023.10.07

1.yo

算法：博弈论+动态规划dp

给出两个字符串 $s \in \{1,2,3,4,5,6,7,8,9\}$，$t \in \{y,o\}$，代表每次由 $t_i$ 来操作，对于一个初始为 $0$ 的数的末尾加入 $0$ 或 $s_i$ 。

如果最后得到的数能被 $11$ 整除，$y$ 胜，否则 $o$ 胜，求最优策略的获胜方。

考虑从后往前进行博弈论 $dp$，设 $dp_{i,j}$ 代表从后往前加到到第 $i$ 个数余数为 $j$ 时 $y$ 是否必胜，转移即为：$(0\le j < 11)$

$\begin{cases}
y: dp_{i,j}=dp_{i+1,(j\times10+s_i)%11}_|dp_{i+1,(j\times10)%11}\ o: dp_{i,j}=dp_{i+1,(j\times10+s_i)%11}_&dp_{i+1,(j\times10)%11}
\end{cases} $

最后判断 $dp_{1,i}$ 是否有必胜状态即可。

2.journey

算法：离线+图论

给出一个 $n$ 个点 $m$ 条边的无向图，定义无向图的行进规则:

当在时刻 $T$ 尝试进入第 $i$ 条边，如果 $T\le i$ 将在 $i$ 时刻出边。
当在时刻 $T$ 尝试进入第 $i$ 条边，如果 $T>i$ 无法进边。

现在给出 $q$ 组询问，每组询问一个四元组 $(l,r,s,t)$，问在时刻 $l$ 到时刻 $r$ 间，$s$ 是否能走到 $t$。如果可以输出 $Yes$，否则输出 $No$。

考虑到走的边是单调递增的，所以我们可以倒叙加边，先将询问的每个 $r$ 插入位置 $l$ 当中，并看两点在边 $[l,m]$ 中最早能走到一起的时间是否小于等于 $r$ 即可。

3.double

算法：倍增dp

4.seal

算法：动态规划dp

有一道门，给出 $n$ 个人的进出门时间 $s,t$，要求在门内时可以随意开门锁门，在门外时开门锁门需要钥匙，只有 $m$ 个人有钥匙，最大化锁门时间。

我们可以先将每个人的进出门时间排序，对于每两个相邻的时间点进行分类讨论：

前一个回，后一个出，无需钥匙
两个回，后一个需要钥匙
两个出，前一个需要钥匙
前一个出，后一个回，需要同时拥有钥匙

这里我们设前一个为 $i$，后一个为 $j$，那么我们可以将这些区间段的贡献添加到点权或边权上。比如当 $i$ 需要钥匙时，我们可以将 $(i,j)$ 段的贡献加在 $i$ 的点权上；当都需要钥匙时，我们可以加在 $(i,j)$ 这条边上。

最后我们将每个时间点连成了一条链，考虑在链上进行 $dp$，定义 $dp_{i,j,0/1}$ 表示上一个人为 $i$ 已经配置了 $j$ 把钥匙时，上一个人是否配置了钥匙，在链上跑 $dp$ 即可。

2023.10.08

1.increase

算法：博弈论+动态规划dp

给出一个 $n$ 个点 $m$ 条边，每条边有一个互不相同的边权，每条路径上的边权必须单调递增。有 $Alice$ 和 $Bob$ 两人在图上来回走边($Alice$ 先手)，$Alice$ 希望走的尽量多，$Bob$ 希望走的尽量少，问当起点 $s$ 为 $[1,n]$ 时能走的最大步数。

思路和 $10.7~journey$ 相似，我们从大往小加边，需要维护两个状态，一个 $A_x$ 表示 $Alice$ 在点 $x$ 上能走的最多步数，另一个 $B_x$ 表示 $Bob$ 在点 $x$ 上能走的最多步数，当我们插入一条 $(u,v)$ 的边就会有转移：

$\begin{cases}A_u=max(A_u,B_v+1) \\ A_v=max(A_v,B_u+1)\\ B_u=max(B_u,A_v+1)\\ B_u=max(B_u,A_v+1)\end{cases}$

以 $i$ 为起点的答案即为 $A_i$。

2.network

算法：树

给出一个 $n$ 个点的树，每个点有黑白两种颜色，初始所有点全为白色，有两种操作：

将一个点 $x$ 染成黑色。
给出 $x$，求 $x$ 到所有黑点的简单路径上最小的下标。

求每次 $2$ 操作的答案。

$n,q$ 同阶时，树链剖分套线段树能够达到 $O(n~log^2~n)$，套 $st$ 表能优化掉一个 $log$，但我们有一种线性 $O(n)$ 的做法。

我们发现每次染成的黑点与之前染过的黑点的简单路径上答案会唯一，所以可以将第一个被染黑的点设为根节点，于是我们对于三点 $root,x,y$ 互相的简单路径简化为 $(root \to x)(root \to y)$。于是我们维护一个 $minn_x$ 表示 $x$ 到根节点的路径上的下标最小值，再维护一个黑点到根路径最小值 $mn$，对于每次染色 $x$ 点处理 $mn$ ： $mn=min(mn,minn_x)$。

再考虑询问点 $x$，如果 $x$ 在某个黑点 $y$ 到根节点的路径上，答案为 $minn_y$，而在一个黑点 $y$ 的子树中，答案为 $minn_x$，所以将 $minn_x$ 与 $mn$ 取 $min$ 即可。

3.stone

算法：动态规划dp

有一个长度为 $n$ 的序列 $a$，我们有以下两种取数规则：

如果 $i=a_i$，可以取完 $a_i$，并让区间 $[1,i-1]$ 的数 $+1$ 。
最小化剩余数。

现在给出一个 $k$，$a_i \in [0,k]$，求序列 $a$的所有情况的剩余数之和。

我们发现每个数只受后面数的影响，从前往后的计算显然不方便处理，所以我们考虑从后往前进行 $dp$。设状态 $f_{i,j}$ 和 $g_{i,j}$ 表示处理到第 $i$ 个数，后面进行的总 $+1$ 操作数为 $j$ 的方案数和权值和，如果此处填的数 $val \le i$，说明可以往后作操作，并且必定会操作 $\left \lfloor \frac{val+j}{i} \right \rfloor $ 次，我们设当前操作次数为 $add$，剩余的石头数为 $hav$，便有转移：

$\begin{cases}f_{i,j+add} \gets f_{i,j+add}+f_{i+1,j} \ g_{i,j+add} \gets g_{i,j+add}+f_{i+1,j} \times hav \end{cases} $

$+1$ 操作数为 $n^2$ 量级，所以状态为 $O(n^3)$，再加上枚举每一位数字的 $O(n)$，最终时间复杂度 $O(n^4)$，跑不满，对于 $n,k\le100$ 的条件绰绰有余。

4.count

算法：动态规划dp

给出一个 $n$ 和 $m$，求有多少种方法构造一个长度为 $n$ 的序列 $c$ 满足 $c_i \in [1,m]$ 且数字 $i$ 不能连续出现超过 $a_i$ 次。$(n\le5\times10^3,m\le 10^5)$

我们设 $f_{i,j}$ 表示第 $i$ 个位置由数字 $j$ 结尾的方案数，那么有基础转移：

\[\begin{aligned}f_{i,j}=\sum\limits_{k=i-a_j}^{i-1}\sum\limits_{x \ne j}^{m}f_{k,x}\end{aligned} \]

时间复杂度 $O(n^2m^2)$，我们可以容斥，设 $S_i=\sum\limits_{k=1}^{i}\sum\limits_{x=1}^{m}f_{k,x}$，那么式子化简为：

\[\begin{aligned}f_{i,j}=S_{i-1}-S_{i-a_j-1}-\sum\limits_{k=i-a_j}^{i-1}f_{k,j}\end{aligned} \]

时间复杂度 $O(n^2m)$，再次设 $g_{i,j}=\sum\limits_{k=1}^{i}f_{k,j}$，那么式子再次化简：

\[\begin{aligned}f_{i,j}=S_{i-1}-S_{i-a_j-1}-(g_{i-1,j}-g_{i-a_j-1,j})\end{aligned} \]

时间复杂度 $O(nm)$，发现 $nm$ 的状态就算是 $O(1)$ 转移也不可行，所以我们可以将所有 $a_i$ 放入一个桶中，将 $dp$ 的状态修改成 $n^2$，再修改对应的转移就可以了，最终时间复杂度 $O(n^2)$。

2023.10.09

1.ak

算法：中位数

给出一个长度为 $n$ 的序列 $a_i$，每次拿连续的 $k$ 个数，直到剩下最后一个数，$Alice$ 希望拿出的数的和尽量小，$Bob$ 希望拿出的数的和尽量大，双方都采用最优策略，求 $Alice$ 先手时拿出的数的和。$(n \equiv1(mod~k))$

因为最后只会剩下一个数，我们设剩下的是 $a_i$，显然答案就为 $sum-a_i$ ，然后我们讨论最后会剩下哪一个数。首先，不是所有数到最后都有留下的可能，只有右边和左边的数字个数都能被 $k$ 整除时才有可能被留下，即为 $1+kx$，接下来就将所有 $1+kx$ 存下来处理一个中位数即可，因为 $Alice$ 先手，所以当可以被留下来的数为偶数时，应选取较大的数。

2.tower

算法：最短路

给出 $n$ 个点，每个点有一个颜色 $b_i \in [1,k]$，定义从 $i$ 点到 $j$ 点的代价为 $|i-j|$，同时有 $S_{i,j}$ 表示颜色为 $i$ 的点是否和颜色为 $j$ 的点两两连接，求 $1$ 到 $n$ 的最短路。

有一个比较明显的贪心思路：如果我们要从点 $x$ 转移到一个颜色为 $c$ 的点，那最优转移到最靠近 $x$ 且颜色为 $c$ 的点，即 $x$ 的左边和右边的第一个颜色为 $c$ 的点。我们先预处理每个位置对于每个颜色的最佳转移点，再直接用这样的转移思路跑 $Dijkstra$，答案即为 $dis_n$。

3.game

算法：莫比乌斯反演

4.loser

算法：树链剖分+线段树

2023.10.10

1.wisdom

算法：模拟

给出一个 $n$ 行 $m$ 列的矩阵，形如下图：$(n,m \le 10^5)$

$\begin{matrix} 1 & 2& 3 & 4\\ 5&6 &7 &8 \\ 9& 10 &11 &12 \end{matrix}$

现在进行 $k$ 次操作，每次让 $x$ 行或列的数乘上 $y$，求最后矩阵上数的和。$(k \le 1000)$

因为 $n,m \le 10^5$，显然不能暴力枚举，考虑从操作的行列入手。因为 $k \le1000$，所以交叉的点最多有 $500 \times 500$ 个，暴力处理即可。

2.matrix

算法: FWT

3.elevator

算法:李超线段树

4.mex

算法：容斥dp

2023.10.11

1.ave

算法：模拟

给出一个长度为 $n$ 的序列，求两两求平均数的最大值。

从小到大排序贪心求平均数即可。

2.sequence

算法: 容斥dp

给出 $n$ 和 $m$，求有多少种序列满足：

$\forall i:a_i \in[1,m] $
$\forall i:a_i \le a_{i+1} ~||~ (a_i\%a_{i+1})>0$

一个明显的思路是定义 $dp_{i,j}$ 表示处理到第 $i$ 个数，最后一个数字是 $j$，转移 $O(nm)$，也可以数论分块优化成 $O(n\sqrt m)$，但对于 $n,m \le 10^5$ 还是难以解决。

需要先从状态上入手，考虑分段转移，但前后的数字并不好记录在状态中，再次考虑容斥。首先发现，一组不合法的解满足 $a_{i+1} \ge 2 \times a_i$，这代表连续的不合法解只限于 $log~m$ 的量级，可以直接枚举，再回到容斥式：新定义 $f(S)$ 为集合 $S$ 不合法的方案数，则有：

\[\begin{aligned} \sum\limits_{S\subseteq\{2,3,4,...n\} }(-1)^{|S|}f(S) \end{aligned}\]

可以预处理一个 $g_x$ 表示长度为 $x$ 的非法解的方案数，转移 $f$ 即可：

    for(int i=1;i<=n;i++)//枚举|S|
	for(int j=i-1;j>=max(i-20,0ll);j--)//枚举非法解的长度
	    f[i]=(f[i]-f[j]*g[i-j]%mod+mod)%mod;

3.ring

算法:动态规划dp

现在有一个 $n$ 个点的环，点权 $p_i$ 是 $[1,n]$ 的排列，求满足下列条件的排列数：

共 $n$ 次操作，第 $i$ 次操作我们把值依次为 $i$ 的点的左右两点交换，设左右两点点权分别为 $a,b(a<b)$，如果存在 $a<i<b$，条件成立。

直接枚举排列的 $O(n^nn)$ 显然不好优化，我们考虑把数字这个要素去掉，尝试转换成某种关系。我们发现已经操作过的数字都是比当前的 $i$ 小的，我们设操作过的点变为黑点，其余为白点，那么不合法的情况便为：某次操作旁边两个都是黑点或白点（都大于它或都小于它）。

我们又发现每次操作形成的黑点到后面永远无法变白，相当于这个黑点将整个白点区间分为了两端。而每一段的数量是可能是奇数和偶数，发现最小的偶数段是一定无解的，而奇数段相反，所以我们可以枚举偶数段进行容斥。

可以设 $dp_i$ 表示长度为 $i$ 的非法情况数，那么当我们在 $j$ 处进行分割时，有转移：

\[\begin{aligned} dp_i=dp_i+dp_{j-1}\times dp_{i-j} \times \begin{pmatrix} i-1\\ j-1 \end{pmatrix} \end{aligned}\]

最后在 $n!$ 所有情况中容斥即可。

4.ds

算法：势能线段树

2023.10.12

1.calc

算法：线性筛

定义 $F(N)=|N-\sum\limits_{d|N}d|$，求 $\sum\limits_{i=A}^{B}F(i)$ 。

首先需要了解求一个数的因数和 $x$ 的式子：

\[\begin{aligned} x=\prod\limits_{i=1}^{r}\sum\limits_{j=0}^{k_i}p_i^j \end{aligned}\]

我们可以记数 $x$ 的因数和为 $f_x$，因为线性筛每次只会筛最小的因数，所以我们再维护一个 $g_x$ 表示数 $x$ 的最小质因数的 $\sum\limits p_i^j $，式子如下：

$i\%p_j \ne 0:\begin{cases} g_{i \times p_j}=g_i \times (p_j+1)\\ f_{i \times p_j}=f_i \times (p_j+1) \end{cases}$
$i\%p_j = 0:\begin{cases} g_{i \times p_j}=g_i \times p_j+1\\ f_{i \times p_j}=\frac{f_i}{g_i} \times g_{i \times p_j} \end{cases}$

因为当不存在质数 $p_j$ 时，我们需要新增一个 $(p_j^0+p_j^1)$，所以会转移一会乘 $(1+p_j)$；而存在 $p_j$ 时，则需要将类似 $(p_j^0,p_j^1...p_j^{k})$ 的部分转换为 $(p_j^0,p_j^1...p_j^{k+1})$ ，所以转移二的 $g$ 操作要先乘 $p_j$ 再加 $1$ 即加 $p_j^0$，转移二的 $f$ 转移即是在更换变换部分的过程。

将所有 $\le B$ 的 $f_x$ 筛出以后，直接计算就行了，时间复杂度 $O(N)$。

2.king

算法: 反悔贪心

给出 $n$ 个 $A$ 物品，和 $m$ 个 $B$ 物品：

每个 $A$ 类物品可以用 $1$ 的代价获得 $a_i$ 的价值。
每个 $B$ 类物品可以用 $1$ 的代价获得 $a_i$ 的价值或 $2$ 的代价获得 $b_i$ 的价值。

我们可以先按照性价比排序，即将 $max(2 \times a_i,b_i)$ 从大到小进行排序，然后依次取。其中争对 $B$ 物品，如果 $b > 2 \times a$ 可以直接将 $b$ 取走，但对于 $b \le 2\times a$ 的情况，我们可以将 $B$ 物品看作用 $1$ 价值获得 $a$，再用 $1$ 价值获得 $b-a$，即先取 $a$，再看升级为 $b$ 在决策中是否更优。

3.au

算法:动态规划dp

4.ttk

算法：图论+卷积

2023.10.13

1.beach

算法：博弈论+动态规划dp

给出一个长度为 $n$ 的字符串 $S \in \{C,P\}$，$A$ 和 $L$ 两人每次可以取走字符串两端的一个字符，先取到 $k$ 个 $C$ 的人失败，问 $A$ 是否有必胜策略。

因为两人轮流操作，所以当我们确定已经操作过的区间之后，当前操作的人能轻松推出，因此我们设 $dp_{l,r,k}$ 为当操作区间为 $[l,r]$ 且当前操作的人拿了 $k$ 个 $C$ 时 $A$ 是否有必胜策略，记忆化搜索即可，时间复杂度 $O(n^3)$。

2.equation

算法: 乘法逆元

给出 $a,d,n,p$，求: $(n\le 10^9)(a,d,n\le10^7)$

\[\begin{aligned} (\prod\limits_{i=0}^{n-1}(a+id))\%p \end{aligned}\]

我们将式子中的 $d$ 提出来变为：

\[\begin{aligned} (d^n\prod\limits_{i=0}^{n-1}(\frac{a}{d}+i))\%p \end{aligned}\]

观察到乘积式是一个阶乘，预处理计算即可，注意特判 $(d,a=0)$ 或 $(\frac{a}{d}+n-1 > p)$。

3.game

算法:博弈论

给出一个有向图，$Alice$ 和 $Bob$ 轮流操作图上的一个点 $x$，设每个点的点权为该点的下标，$Alice$ 需要最大化经过点的点权最大值，$Bob$ 需要最小化最大值，游戏将在操作 $10^{100}$ 次后结束，当 $x$ 为 $[1,n]$ 时能经过的点权最大值。

一般的博弈论只会有输赢平三种情况，但这道题的博弈论求的是一个具体的数值，显然是不好处理的。所以我们先考虑枚举答案 $ret$，看从哪些点开始能够取到 $ret$。

实际上我们是维护了一个区间，一个 $S \in\{f_i\ge ret\}$，另一个 $T \in\{f_i< ret\}$。考虑直接按点权从小到大加点，尝试扩展 $S$。现在还有一个难点，在于 $Alice$ 和 $Bob$ 的转移。发现 $Alice$ 为先手的 $f_u$ 会取到 $max\{f_v\}$，而 $Bob$ 先手会取 $max(f_u,min\{f_v\})$，所以我们直接维护两种类型的点，我们称他们为 $Alice$ 点和 $Bob$ 点。进行以下操作即可：

对于 $u \to v$，反向建边 $v_B \to u_A$，$v_A \to u_B$。
从大到小枚举 $ret$，将点权等于 $ret$ 的点加入集合 $S$。
尝试用集合 $S$ 中的点去影响集合 $T$ 中的 $Alice$ 点。
当尝试影响的点 $v$ 的入度为 $0$ 时，可以影响到 $v_B$。

2023.10.21.CSP-S

posted @ 2024-01-12 16:40 Chax 阅读(112) 评论(0) 收藏举报

刷新页面返回顶部

Chx的博客

2023解题报告(CSP-S前)

2023.06.17

1.b

2.乘积筛

3.国战

4.烤串

2023.07.03

1.最小基因序列

2.等差数列

3.策略游戏

2023.07.05

1.舞

2.此后

3.选择

2023.07.07

1.异或平方和

2.除雪

3.天堂之战

2023.07.10

1.城市天际线

2.景点距离

3.排列

2023.07.12

1.生命游戏

表示要求这个格子有生命，.表示要求没有。

2.Bajka

3.序列修改

2023.07.14

1.valk

2.selotejp

3.papricice

2023.07.17

1.patkice

2.内鬼

3.诡意行商

2023.07.19

1.原题

2.撰写博客

3.顶级厨师

2023.08.07

1.骰子游戏

2.裁剪彩带

3.挑战 NPC

2023.08.09

1.genshin

2.arknights

3.arena

4.rail

2023.08.11

1.perm

2.tree

3.network

4.lis

2023.08.12

1.lock

2.path

3.xor

4.subgraph

2023.08.14

1.up

2.family

3.love live

4.izumi

2023.08.16

1.de

2.motive

\(f(l,r,p)=\sum\limits_{i=l}^p \sum\limits_{j=p}^r \frac{[j-i \ge 2]}{j-i-1}\)

\(h(l,r)=\sum\limits_{i=l}^r \sum\limits_{j=i}^r \frac{[j-i \ge 2]}{j-i-1}\)

\(f(l,r,p)=h(lr)-h(l,p)-h(r,p)\)

3.math

4.interval

2023.08.18

1.sequence

2.puxi

3.gnsi

4.tree

2023.08.19

1.sequence II

2.math II