密码工程-扩展欧几里得算法

任务详情

0. 在openEuler(推荐)或Ubuntu或Windows(不推荐)中完成下面任务，要用git记录实现过程，git commit不能低于5次
1. 严格按照《密码工程》p112伪代码实现ExtendedGCD（int a, int b, int *k, int *u, int *v）算法（10')
   2.根据ExtendedGCD 实现计算模逆元的函数int modInverse(int a, int m) ，返回a相对于m的模逆元（3‘）
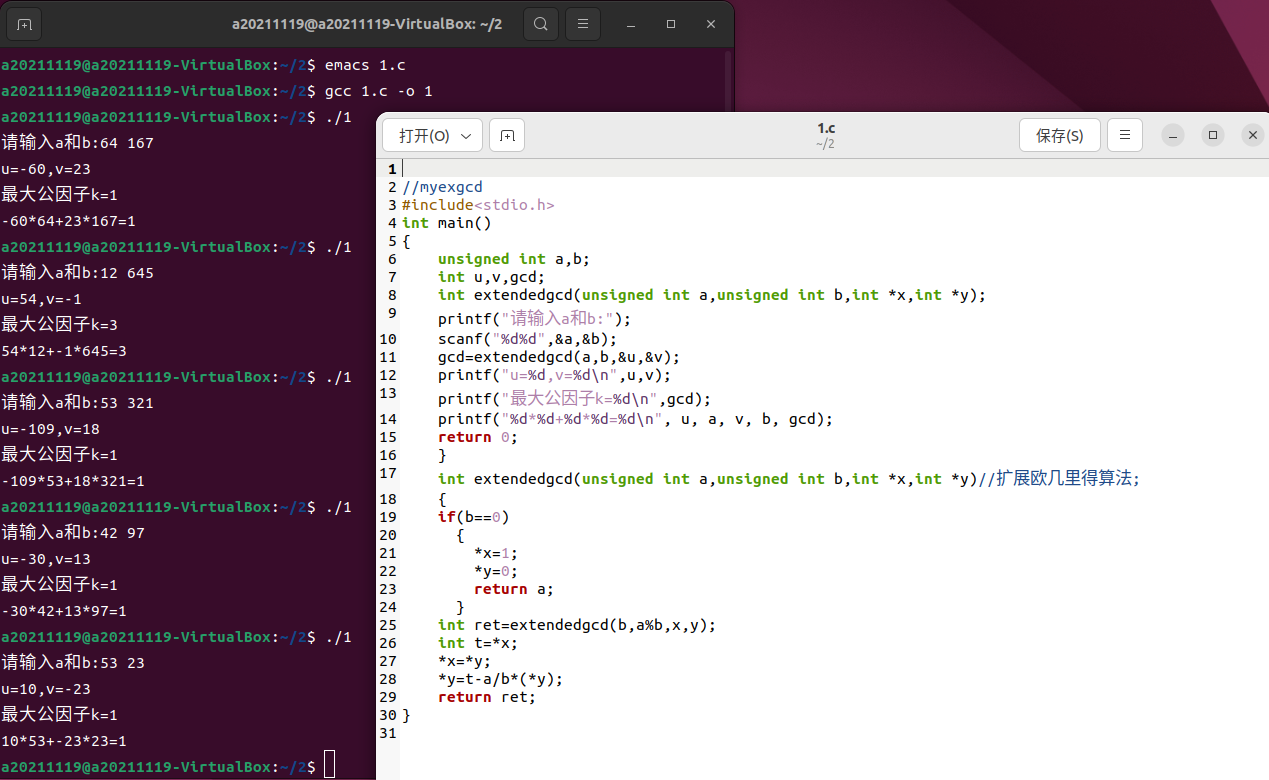
2. 在测试代码中计算74模167的模逆元。自己再设计至少两个类似测试代码。（2’）
3. 提交代码和运行结果截图，git log截图
4. 提交使用Markdown并转为pdf格式，或者使用doc、docx格式

严格按照《密码工程》p112伪代码实现ExtendedGCD（int a, int b, int *k, int *u, int *v）算法（10')

#include<stdio.h>
int main()
{
    unsigned int a,b;
    int u,v,gcd;
    int extendedgcd(unsigned int a,unsigned int b,int *x,int *y);
    printf("请输入a和b:");
    scanf("%d%d",&a,&b);
    gcd=extendedgcd(a,b,&u,&v);
    printf("u=%d,v=%d\n",u,v);
    printf("最大公因子k=%d\n",gcd);
    printf("%d*%d+%d*%d=%d\n", u, a, v, b, gcd);
    return 0;
    }
    int extendedgcd(unsigned int a,unsigned int b,int *x,int *y)//扩展欧几里得算法;
    {
    if(b==0)
      {
        *x=1;
        *y=0;
        return a;
      }
    int ret=extendedgcd(b,a%b,x,y);
    int t=*x;
    *x=*y;
    *y=t-a/b*(*y);
    return ret;
} 

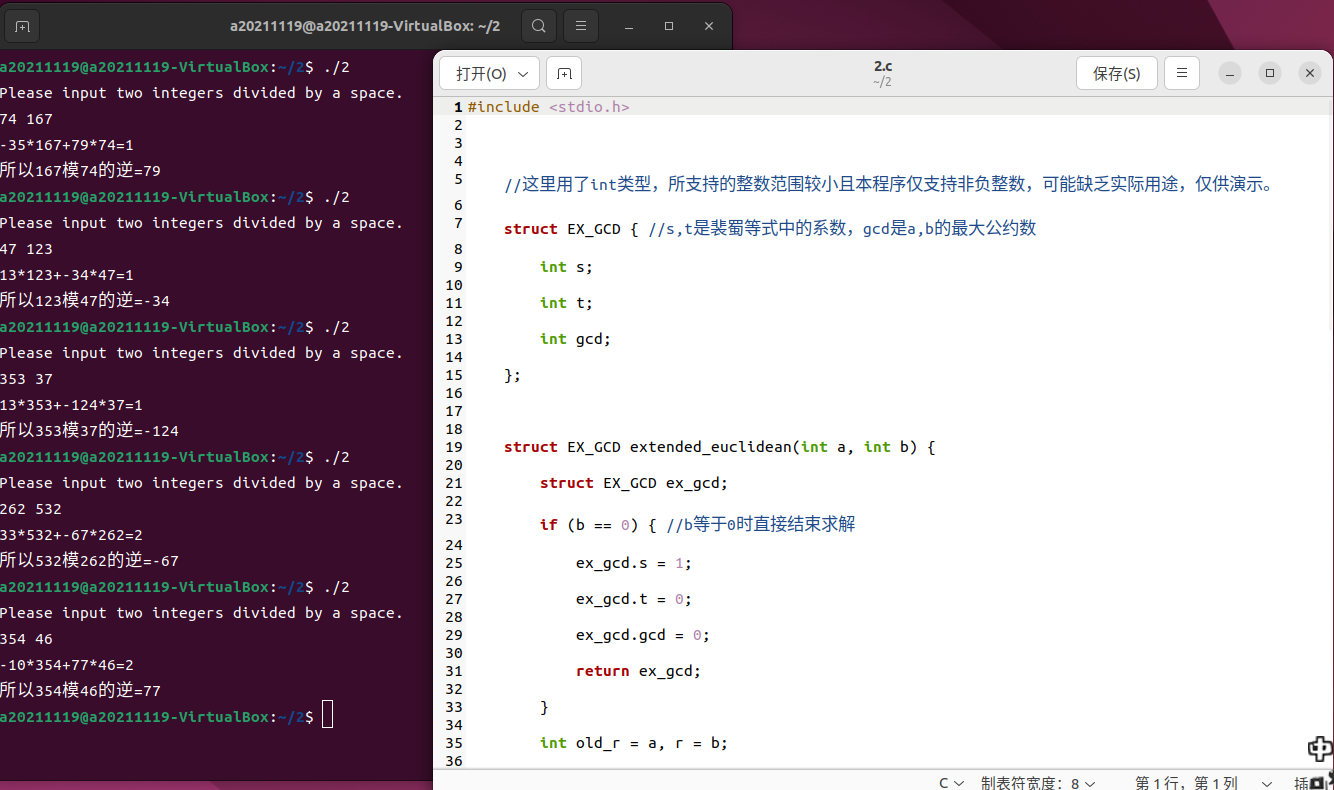
根据ExtendedGCD 实现计算模逆元的函数int modInverse(int a, int m) ，返回a相对于m的模逆元（3‘）

#include <stdio.h>

     

    //这里用了int类型，所支持的整数范围较小且本程序仅支持非负整数，可能缺乏实际用途，仅供演示。

    struct EX_GCD { //s,t是裴蜀等式中的系数，gcd是a,b的最大公约数

        int s;

        int t;

        int gcd;

    };

     

    struct EX_GCD extended_euclidean(int a, int b) {

        struct EX_GCD ex_gcd;

        if (b == 0) { //b等于0时直接结束求解

            ex_gcd.s = 1;

            ex_gcd.t = 0;

            ex_gcd.gcd = 0;

            return ex_gcd;

        }

        int old_r = a, r = b;

        int old_s = 1, s = 0;

        int old_t = 0, t = 1;

        while (r != 0) { //按扩展欧几里得算法进行循环

            int q = old_r / r;

            int temp = old_r;

            old_r = r;

            r = temp - q * r;

            temp = old_s;

            old_s = s;

            s = temp - q * s;

            temp = old_t;

            old_t = t;

            t = temp - q * t;

        }

        ex_gcd.s = old_s;

        ex_gcd.t = old_t;

        ex_gcd.gcd = old_r;

        return ex_gcd;

        }

     

    int main(void) {

        int a, b;

        printf("Please input two integers divided by a space.\n");

        scanf("%d%d", &a, &b);

        if (a < b) { //如果a小于b，则交换a和b以便后续求解

            int temp = a;

            a = b;

            b = temp;

        }

        struct EX_GCD solution = extended_euclidean(a, b);

        printf("%d*%d+%d*%d=%d\n", solution.s, a, solution.t, b, solution.gcd);

        printf("所以%d模%d的逆=%d\n", a,b,solution.t);

        return 0;

    }