二分的基础性学习

临近NOIP，身为蒟蒻的我开始了基础知识的回顾，希望可以拿到弱省的一个一（二）等奖orz

今天学习的是二分答案！

当我们做题是发现题目的描述中出现了：最大值最小   最小值最大    这两种说法时，我们就应当注意了，这个题目使用二分的几率是达到80%~90%的。

下面是二分的基础伪代码：

int left,right;
left=1,right=n;
while(left<=rignt)
{
    int mid=(left+right)/2;
    if(judge(mid)==false) //判断mid这个值成不成立
         left=mid+1;
    else right=mid-1;
}
//最后的答案是left或right，根据题目

 当然在c++中，我们用二分查找时有两个函数可以使用（忘记别的语言有没有了...）

就是 upper_bound()和lower_bound() ​​​​​​​

 

 

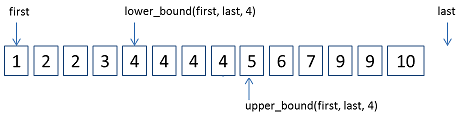
lower_bound(f,f+n+1,x)  返回不下降序列里第一个大于等于x数的 地址 所以使用时用int变量存储是应如下定义

int t=lower_bound(f,f+n1,x)-f;

int t=upper_bound(f,f+n+1,x)-f;

upper_bound(f,f+n+1,x) 同理，返回不下降序列里第一个大于x的数的地址

上述两个函数运行时使用二分的思想，所以查找一次的复杂度是O(nlogn)的。

注：使用二分查找只适用于顺序存储结构，包括上述两个函数

 

推荐一道经典题目：导弹拦截  洛谷数据加强版

使用二分O（nlogn）的复杂度求最长不下降子序列拿到200分哦

关于这个题的题解刚刚安排上了（挖个坑先）