Educational Codeforces Round 185 (Rated for Div. 2)
A. Maximum Neighborhood
void solve(){ int n; cin >> n; if(n == 1) { cout << 1 << endl; return ; } if(n == 2){ cout << 9 << endl; return ; } int t1 = 4 * n * n - n - 4; int t2 = 5 * n * n - 5 * n - 5; cout << max(t1, t2) << endl; }
B. Addition on a Segment
这样想,如果每次都是选一个区间,那么n次操作后,数组 a 的和就是 n。一旦计算得到数组 a 的和大于 n,则说明存在至少一个操作选的区间是大于1的,这一次操作能取到的最大值取决于 a 数组总和减去 n,并且最长不会超过数组 b 不为0的元素的长度;也就是说,取一个最长区间,总有n-1次操作能达到题目的要求。
void solve(){ int n; cin >> n; int sum = 0, x; int len = 0; for(int i = 0; i < n; ++i){ cin >> x; if(x) len++; sum += x; } cout << min(sum - n + 1, len) << endl; }
C. Quotient and Remainder
根据题目可推出上述不等式 ,为了尽可能得最大操作次数,我们将 (k - ri) / (ri + 1) 从大到小遍历,在b数组中搜索,一旦发现有比这个数小于等于的元素,说明符合题目要求,删除b数组的这个元素,ans++,直至 ri 遍历结束,得到答案。
void solve(){ int n, k; cin >> n >> k; vector<int> q, r(n + 1); for(int i = 1; i <= n; ++i){ int x; cin >> x; q.emplace_back(x); } for(int i = 1; i <= n; ++i) cin >> r[i]; vector<int> a; for(int i = 1; i <= n; ++i) a.emplace_back((k - r[i]) / (r[i] + 1)); sort(q.begin(), q.end()); sort(a.begin(), a.end()); int i = 0, j = 0; int ans = 0; while(i < n && j < n){ if(q[i] > a[j]) j++; else{ ans++; i++; j++; } } cout << ans << endl; }



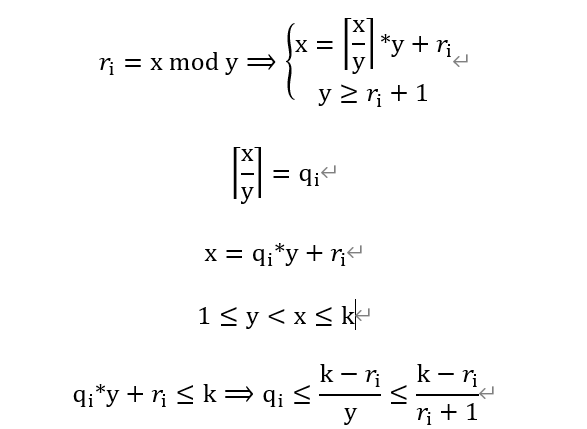

 浙公网安备 33010602011771号
浙公网安备 33010602011771号