树状数组
参考:y树状数组 - OI Wiki
1.常见的树状数组是一种支持单点修改,区间查询的数据结构,下面给出模版
int lowbit(int x) { return x & -x; }我们记 𝑥
二进制最低位
1以及后面的0组成的数为 lowbit(𝑥)注意:lowbit
指的不是最低位
1所在的位数 𝑘,而是这个
1和后面所有0组成的 2𝑘。
所以树状数组的索引最低位从1开始,因为索引为0时lowbit不存在,若题目中范围有取到0,记得向右偏移规避索引为0的情况。
void add(int x, int k) { x++; while (x < N) { tree[x] += k; x += lowbit(x); } }此函数方法主要用来实现单点修改,在 x 的位置上加入 k ,在构建树状数组时,常用于添加每个位置上的数构建树状数组。
int getSum(int x) { x++; int res = 0; while (x > 0) { res += tree[x]; x -= lowbit(x); } return res; }此函数主要用来实现区间访问,返回 区间 [1, x] 上区间和。
#include<bits/stdc++.h> using namespace std; #define int long long const int N = 5e5 + 5; int tree[N]; int lowbit(int x) { return x & -x; } void add(int x, int k) { x++; while (x < N) { tree[x] += k; x = x + lowbit(x); } } int getSum(int x) { x++; int res = 0; while (x > 0) { res += tree[x]; x -= lowbit(x); } return res; } void solve() { int n, m; cin >> n >> m; int t; for (int i = 1; i <= n; ++i) { cin >> t; add(i, t); } int op, x, y, k; for (int i = 1; i <= m; ++i) { cin >> op; if (op == 1) { cin >> x >> k; add(x, k); } else { cin >> x >> y; cout << getSum(y) - getSum(x - 1) << endl; } } } signed main() { ios::sync_with_stdio(false); cin.tie(0); solve(); return 0; }题目中要求
将某一个数加上 x; ------》 单点修改
求出某区间每一个数的和。 --------》区间访问
上面已经介绍getSum函数返回 [1, x] 区间和,先要求求区间 [l, r] 区间和, 利用前缀和知识 Sum([l, r]) = getSum(r) - getSum(l - 1);
2.还有一种树状数组要求区间修改,单点查询,这样的要求如何转化为传统方法求解呢?
对于单点查询,我们可以利用差分和前缀和的思想,定义差分数组
对于区间修改,根据差分的性质,只需对区间两边进行修改就行
#include<bits/stdc++.h> using namespace std; #define int long long const int N = 5e5 + 5; int tree[N]; int lowbit(int x) { return x & -x; } void add(int x, int k) { x++; while (x < N) { tree[x] += k; x += lowbit(x); } } int getSum(int x) { x++; int res = 0; while (x > 0) { res += tree[x]; x -= lowbit(x); } return res; } void solve() { int n, m; cin >> n >> m; vector<int> a(n + 1, 0); for (int i = 1; i <= n; ++i) { cin >> a[i]; add(i, a[i] - a[i - 1]); } int op, x, y, k; for (int i = 1; i <= m; ++i) { cin >> op; if (op == 1) { cin >> x >> y >> k; add(x, k); add(y + 1, -k); } else { cin >> x; cout << getSum(x) << endl; } } } signed main() { ios::sync_with_stdio(false); cin.tie(0); solve(); return 0; }



 二进制最低位
二进制最低位 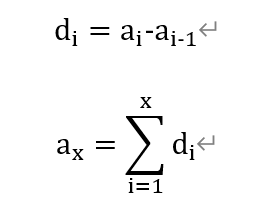

 浙公网安备 33010602011771号
浙公网安备 33010602011771号