牛顿迭代法
一、导数


导数可以理解为某点的斜率。
泰勒公式:

在x -> x0的情况下,可以看成是:
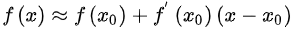
这也是后面牛顿迭代法所用到的公式
二、牛顿迭代法
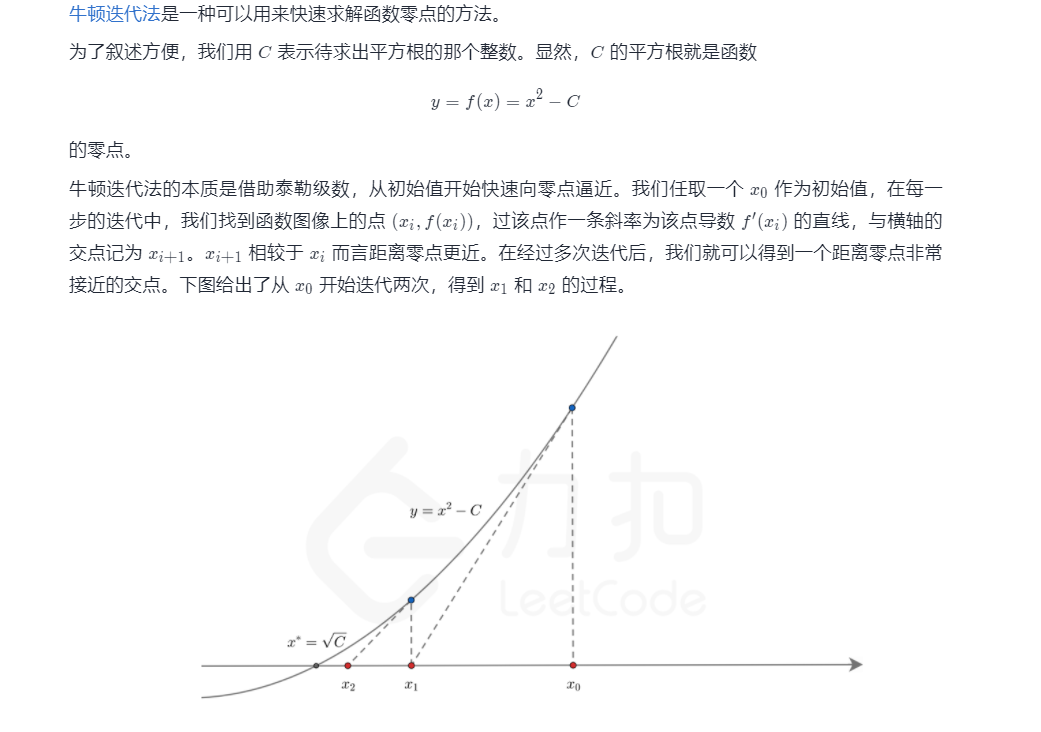
通过不断迭代,逐渐逼近零点,当迭代点X(n-1) - Xn -> ε 无穷小时,可以认为得到该解;
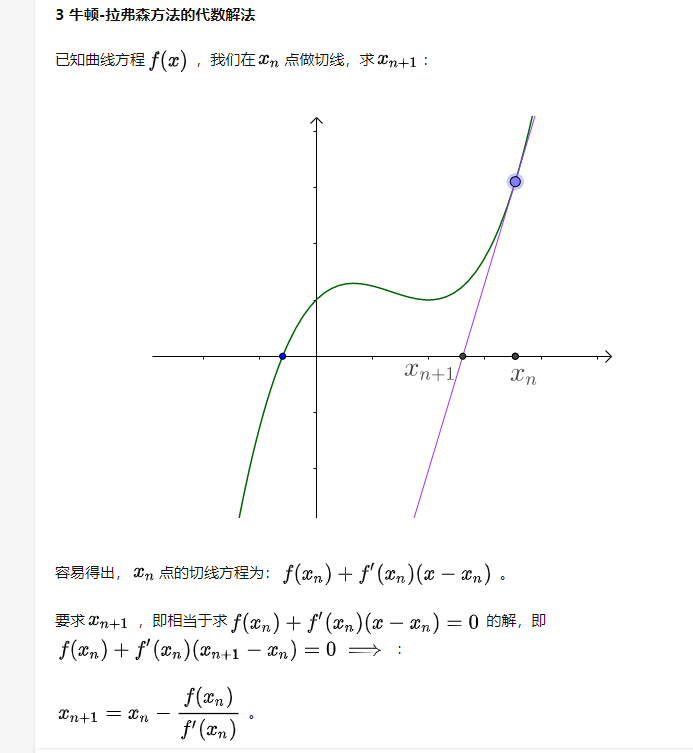
三、牛顿迭代应用
(1)https://leetcode-cn.com/problems/sqrtx/solution/x-de-ping-fang-gen-by-leetcode-solution/ 69. Sqrt(x) 求解x的平方更
class Solution {
public int mySqrt(int x) {
if (x == 0) {
return 0;
}
double C = x, x0 = x;
while (true) {
double xi = 0.5 * (x0 + C / x0);
if (Math.abs(x0 - xi) < 1e-7) {
break;
}
x0 = xi;
}
return (int) x0;
}
}
(2)https://www.nowcoder.com/practice/caf35ae421194a1090c22fe223357dca?tpId=37&&tqId=21330&rp=1&ru=/ta/huawei&qru=/ta/huawei/question-ranking

import java.util.Scanner;
public class Main{
public static void main(String[] args){
Scanner input = new Scanner(System.in);
while (input.hasNextDouble()){
double num = input.nextDouble();
double x = 1.0;
for (; Math.abs(Math.pow(x,3)-num)>1e-3; x=x-((Math.pow(x,3)-num)/(3*Math.pow(x,2))));
System.out.println(String.format("%.1f", x));
}
}
}
参考:
https://www.zhihu.com/question/264955988
https://www.zhihu.com/question/20690553


 浙公网安备 33010602011771号
浙公网安备 33010602011771号