特征选择

1、子集搜素与评价

在实际生活中一个样本或许有很多属性，例如一个西瓜样本，有色泽、敲声、纹理、触感等等。但有经验的人往往只看敲声或者纹理。其实并不是所有的特征都是有用的，大多数情况下是一部分有用，这一部分称为“”相关特征”，另外一部分没什么用的称为“无关特征”。从给定集合中选择出相关特征子集的过程称为特征选择。

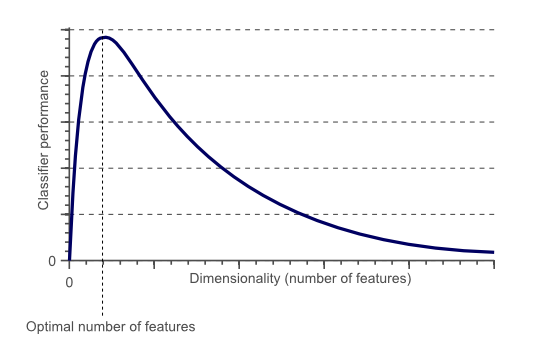
用个图(图片来自wiki)来形象的说明维数灾难，下图可以看到，随着选择的特征数的增大，聚类模型效果在中间某个合适的特征子集达到最大，随后随着特征数的增大下降。若能选择出这个重要特征子集，后续学习过程只需在这个子集特征上进行建模，则维数灾难问题会大大减轻。去除不相干的特征会降低学习任务的难度。

我们今天要做的就是如下图的工作：

如何从原始的特征集选择出重要特征子集？如有领域知识作为先验假设就直接用，比如有某个小学学生数据特征集为年龄、身高、体重、户籍、联系电话、生日等。若要研究年龄身高体重的规律则我们知道与户籍、电话、生日是无关的，即选择年龄、身高、体重特征子集作为相关特征研究即可。

如若没有领域知识作为先验假设，则只能遍历所有可能的子集，然鹅这个工作量是非常大的，常常因为组合爆炸进行不下去，所以有一个可行的做法就是产生一个“候选子集”然后进行评价，基于评价产生下一个“候选子集”，进行评价......直到无法再找到比上一个子集更好的候选子集为止。到这来就产生两个要解决的问题：

（1）如何根据评价选取候选子集？

（2）如何评价候选子集的好坏？

选取子集：

假设给定特征集合为：{ ${a_{1},a_{2},a_{3}...,a_{d}}$ } ,

向前搜索：将每一个特征看作一个单独的候选子集，然后对这 d 个特征子集进行评价，选取最高分胜出。假定 { $a_{2}$ } 得分最高，然后在上一轮的选定集中加入一个特征，产生 d-1 组候选子集，然后进行评分。假定 { $a_{2},a_{3}$ } 得分最高，然后加入一个........，直到加入一个特征评分不如上一次的选定子集，停止生成候选子集，选取上一轮的特征子集为特征选择结果。如下图：

向后搜索：将所有特征看作一个集合，然后评分；再去掉一个特征得到 d-1 组特征集，进行评分；......；直到删去任意一个的评分小于上一轮，结束，选取上一轮的结果作为特征选择结果。

双向搜索：同时进行向前、向后搜索。优点，省时间。

很明显，上述做法是贪心策略，每次只顾本轮得分最高，并不考虑全局。假设本轮 { $a_{2},a_{3}$ }最优，下一轮 { $a_{4},a_{7},a_{5}$ } 比任何的 { $a_{2},a_{3},a_{i}$ } 组合都优。应该是个动态规划问题。虽然贪心不能做到最优，但可能接近最优。遗憾的是，若不进行穷举搜索，则这样的问题无法避免（这句是机器学习清华大学出版社周志华版原话）。

子集评价：

这里介绍一种评价方法：信息增益。其实其他能判断两个划分差异的机制都能用于特征子集评价。假设数据是离散的。

信息增益公式： $G(x_{i})=H(Y)-H(Y|x_{i})$

解释：Y为标签，对于属性 $x_{i}$ ，系统在有它与没它时的信息量的差值就是能给系统带来的信息增益。

信息熵公式： $H(x_{i})=\sum p(x_{ij})*I(x_{ij})$

解释：i 用来区分属性，j 用来区分第 i 属性第 j 类。说的有点复杂了，比如呢！第 i 个属性为性别，取值有男女两种，那么 j 就可以取值为1,2；信息熵就是信息量的期望值。

信息量： $I_{i}=- log_{a} p_{i}$

贴一张图：

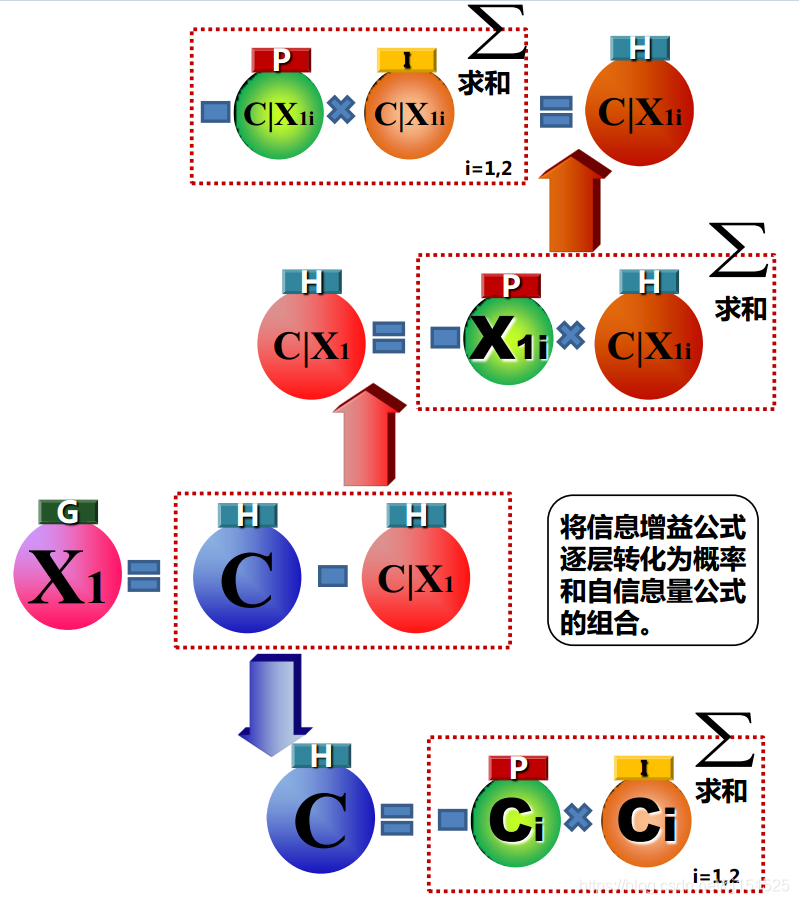
对于属性子集A,根据属性子集A的取值，将数据集D分为V了子集，{ $D^{1},D^{2},D^{3}.....D^{V}$ } ,于是就可以算子集A的信息增益：

$Gain(A)=Ent(D)-\sum_{v=1}^{V}(|D^{v}|/|D|)Ent(D^{v})$

其中信息熵定义为：

$Ent=-\sum_{k=1}^{|y|}p^{k} log_{2}p_{k}$

信息增益越大，意味着特征子集A包含有助于分类的信息越多。因此可以以信息增益为评分标准。

2、常见特征选择方法

（1）过滤式选择(Relief)

对数据进行特征选择，再进行训练学习，选完特征后后续学习与前面特征选择无关。该方法设计一个“相关统计量”来度量特征的重要性，统计量是一个向量。每一个分量对应于一个初始的特征，如下图：

特征	a1	a2	a3	....	an
相关统计量	2	-4	7		-3

特征子集的重要性由子集中每个特征对应的相关统计量分量之和来决定。最终指定一个阈值 $\tau$ ，然后选择大于 $\tau$ 的特征子集对应的相关统计量之和。也可指定特征个数k，选择k特征子集相关统计量和最大的一个。

显然，Relief的关键是确定相关统计量。易知Relief算法的核心在于如何计算出该相关统计量。对于数据集中的每个样例xi，Relief首先找出与xi同类别的最近邻与不同类别的最近邻，分别称为猜中近邻（near-hit）与猜错近邻（near-miss）。

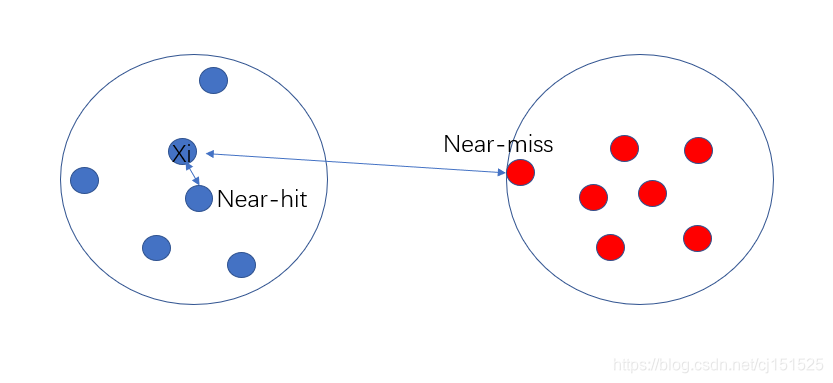
接着便可以分别计算出相关统计量中的每个分量。对于j分量：（已知类别标签，二分类）

è¿éåå¾çæè¿°

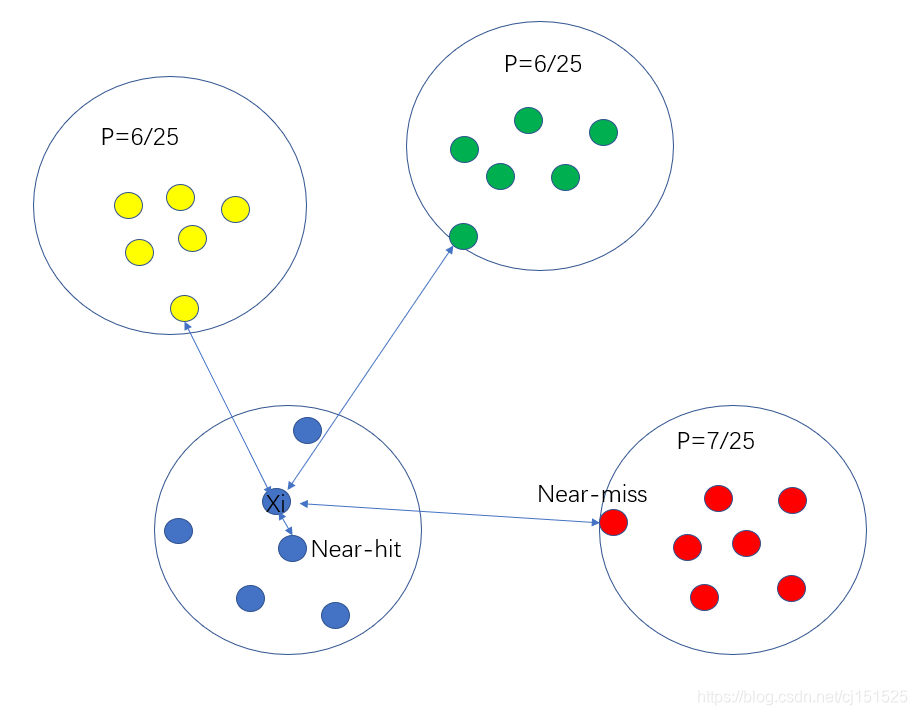
直观上理解：对于猜中近邻，两者j属性的距离越小越好，对于猜错近邻，j属性距离越大越好。更一般地，若xi为离散属性，diff取海明距离，即相同取0，不同取1；若xi为连续属性，则diff为曼哈顿距离，即取差的绝对值。分别计算每个分量，最终取平均便得到了整个相关统计量。标准的Relief算法只用于二分类问题，后续产生的拓展变体Relief-F则解决了多分类问题。对于j分量，新的计算公式如下：

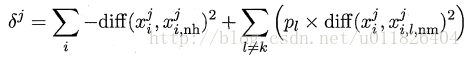
è¿éåå¾çæè¿°