Loading

【Joint Search-and-Training】2020-IJCAI-Beyond Network Pruning a Joint Search-and-Training Approach-论文阅读

Joint Search-and-Training

2020-IJCAI-Beyond Network Pruning a Joint Search-and-Training Approach

来源：ChenBong 博客园

  • Institute：Xidian University
  • Author：Xiaotong Lu，Weisheng Dong*
  • GitHub：/
  • Citation：/

Introduction

提出了一种联合搜索-训练的紧凑网络训练方法，无需使用pre-train model，直接从头开始在backbone网络上搜索-训练紧凑网络。

将backbone网络视为搜索空间，反复搜索、训练不同的子网，将最佳子网取出微调到收敛。


Motivation

传统的剪枝方法：

  • 需要训练一个过度参数化的网络（需要预训练模型），作为剪枝对象
  • 剪枝后需要继承结构和权重

本方法：

  • 把剪枝看做NAS的一个特例
  • 在backbone网络上反复搜索，训练不同的子网

Contribution


Method

Pipeline

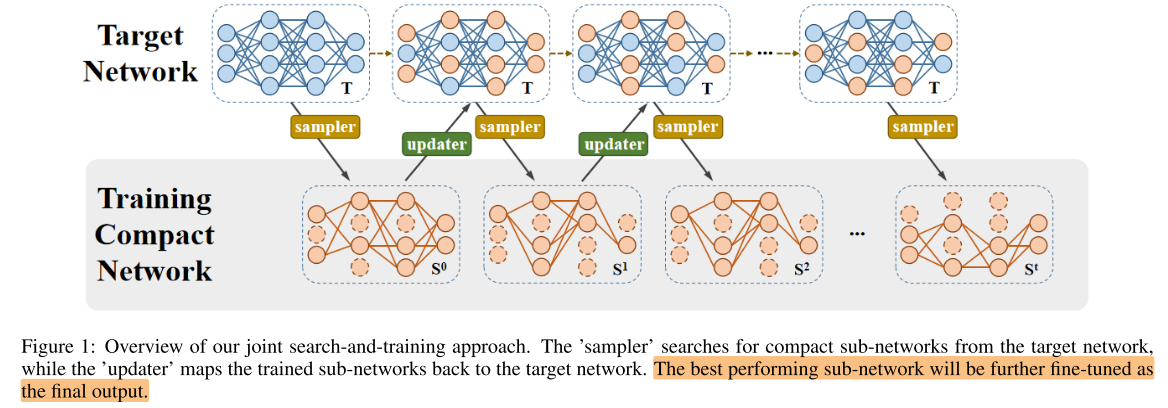
image-20200803170224376

图1说明：

在backbone网络T上反复采样子网络，更新子网络的权重，并将子网络的更新map回backbone网络T中，反复多次后，取出最佳子网络fine-tune到收敛。


Fix pruning rate vs. Our method

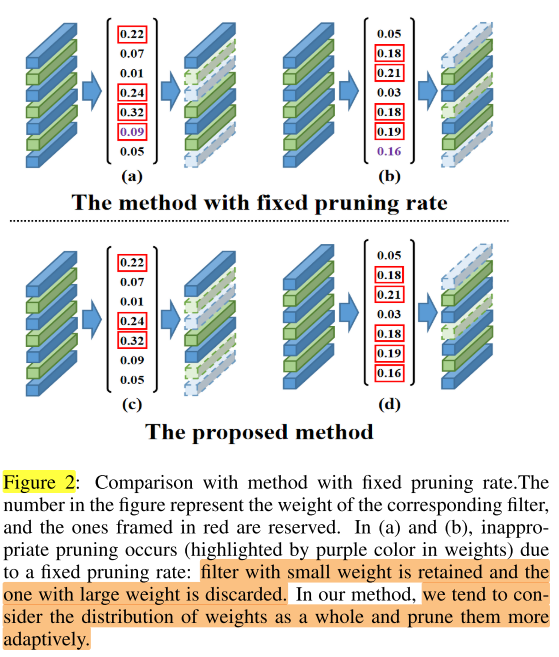
image-20200803170239585

图2说明：

每个filter对应一个 \(\alpha\) ，类似filter的重要性指标，

fix pruning rate是每一层都使用固定的剪枝率，会导致将有的层的某个filter重要性指标较大，但是因为该层未达到指定剪枝率，而把该filter剪掉；

本文的方法类似全局剪枝：

  • 全局剪枝是将重要性小于阈值的filter剪掉，而且全局的阈值是统一的；
  • 本文的方法是每一层对应一个“阈值”，将每层的卷积核重要性大到小排列，将每个卷积核的重要性从头开始逐一累加，当累加到大于该层的“阈值”时停止，此时保留的卷积核即已经累加的卷积核。

ThresNet-每层阈值的计算

image-20200803171321356

\(\beta=\Phi\left(\alpha\right) \qquad(2)\)

公式（2）说明：

  • \(\Phi\) 表示 ThresNet 的参数
  • \(\alpha\) 表示 backbone网络的结构参数（weights）
  • \(\beta\) 表示 backbone网络的各层阈值

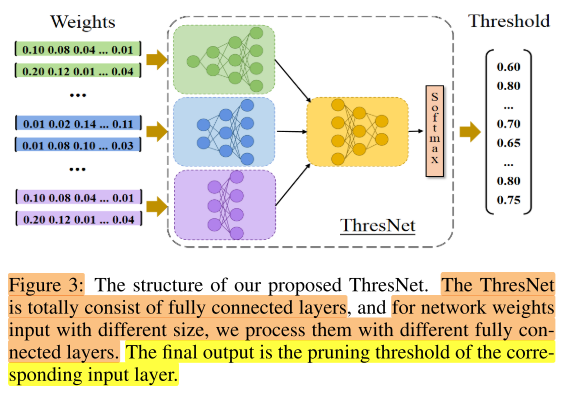
图3说明：

训练一个代理网络ThresNet，作用是根据backbone网络的不同状态（不同时刻，backbone网络的 \(\alpha\) 不同），计算该状态下backbone网络的各层filter的阈值 \(\beta^{l}\) 。

  • 网络输出：各层的阈值 \(\beta\) （e.g. T为16层，则输出为16维的向量）；

    输出是维度是固定的（e.g. 长度=16的向量）

  • 网络输入：各层的结构参数 \(\alpha\)（weights）；

    但输入的维度是不固定的（输入是16个向量，每个向量的长度=对应层的通道数），如一个backbone网络共有3种通道数（如16/32/64），那么输入的一组向量有的是16维，有的是32维，有的是64维，ThresNet网络分为2部分，第一部分就设置3个全连接网络，接收这3种不同维度的向量，将维度都统一到128；第二部分（应该）也是一个全连接网络，输入为3个128维的向量，输出为1个向量（e.g. 16维的向量，代表backbone网络16层每层的阈值）

  • ThresNet 使用强化学习进行训练，是在搜索-训练的过程中逐渐训练的，因此ThresNet也会随着 搜索-训练 的进行，而不断更新ThresNet的网络权重 \(\Phi\)

&& 为什么不能直接将 \(\alpha\) 展开成一维向量？同一个backbone网络，展开后的长度（即filter数量）应该也是固定的吧？


\(\left.R=-\left(l_{a v g}+\gamma \times \operatorname{param}(S)\right)\right) \qquad (3)\)

公式（3）说明：

R为训练ThresNet的奖励Reward


\(\nabla_{\Phi} J(\Phi) \approx \frac{1}{K} \sum_{k=1}^{K} \sum_{l=1}^{L} R_{k} \nabla_{\Phi} \log \pi_{\Phi}\left(\beta^{l} \mid \alpha^{l}\right) \qquad (4)\)

公式（4）说明：

&& 强化学习更新ThresNet的网络权重 \(\Phi\)

&& 应该是训练完 ThresNet 再进行 搜索-训练


算法细节

image-20200803181007793

A2.s1 初始化 backbone 网络

\(\mathbb{O}^{l}=\operatorname{Concat}\left(\mathbb{I}^{l} * W_{1}^{l}, \mathbb{I}^{l} * W_{2}^{l}, \cdots, \mathbb{I}^{l} * W_{\mathbb{C}_{l}}^{l}\right) \qquad (5)\)

公式（5）说明：

  • \(\mathbb{I}^{l}\) 表示第 l 层的输入feature map
  • \(W^l_c\) 表示第 l 层的第 c 个filter
  • *代表卷积操作

\(\mathbb{O}^{l}=\operatorname{Concat}\left(\mathbb{I}^{l} * \hat{\alpha}_{1}^{l} W_{1}^{l}, \mathbb{I}^{l} * \hat{\alpha}_{2}^{l} W_{2}^{l}, \cdots, \mathbb{I}^{l} * \hat{\alpha}_{C_{l}}^{l} W_{C_{l}}^{l}\right) \qquad s.t. \hat{\alpha}_{c}^{l}=\frac{\exp \left(\alpha_{c}^{l}\right)}{\sum_{k=1}^{C_{l}} \exp \left(\alpha_{k}^{l}\right)} \qquad(6)\)

公式（6）说明：

  • 引入结构参数\(\alpha\)，\(\alpha_c^l\) 对应第 l 层第c个filter
  • \(\hat{\alpha}\) 代表softmax后的 \(\alpha\)

kaiming normal 初始化网络T的权重W（parameter）和结构参数 \(\alpha\)（weight）

image-20200803181007793

A2.s3 粗训练 backbone 网络

\(\begin{aligned} \ell_{\text {coarse}}=& \text {CrossEntropyLoss}\left(y_{i}, \mathcal{T}\left(x_{i}, \Omega, \alpha\right)\right) +\lambda\|\alpha\|_{2} \end{aligned} \qquad(1)\)

公式（1）说明：

  • T是大网络（搜索空间）
  • \(\Omega\) 是网络权重（parameter），即上面的W
  • \(\alpha\) 是结构参数
  • \(\lambda\) 是超参

使用以上的loss粗训练网络100个epochs（for cifar），或40个epochs（for ImageNet）


A2.s4~s12 反复搜索（采样）与训练子网络

image-20200803181007793
A2.s5 采样子网络

重复采样T个子网络，实验中（T=30 for cifar，T=20 for ImageNet）

采样是逐层地采样，每一层都采样完即可组成一个子网络。

image-20200803165326149

算法1说明：

  • 输入：l 层的 \(\alpha^l\) 和 filter \(W_{1,2, \ldots, \mathrm{C}_{l}}^{l}\) ，\(C_l\) 是 l 层的通道数
  • 输出：子网络filter的结构参数：\(p^{l}\) ，子网络的 filter \(W_{1,2, \ldots, F_{l}}^{l}\)
  • 步骤：
    • A1.s1 给 \(\alpha^l\) 添加随机扰动，扰动后的结构参数记为 \(n^l\)
    • A1.s2计算 \(n^l\) 的softmax，记为 \(\hat{n}^l\)
    • A1.s3 使用ThresNet 计算 l 层的阈值 \(th^{l}\)
    • A1.s4~s5 将 l 层的卷积核按 \(\hat{n}^l\) 的大小逐一累加，直到累加和大于阈值 \(th^{l}\) 停止，此时累加的个数为c
    • A1.s6 取向量 \(\alpha^l\) （ \(C_l\) 维）的前c个元素，组成新向量 \(p^{l}\) （c维）
    • A1.s7 保留前c个filter

每一层都采样完即可组成一个子网络。


image-20200803181007793
A2.s6~s11 训练子网络

子网络有2组参数，一组是网络权重 \(\Theta\) ，一组是结构参数 \(\alpha\)

在 \(\mathbb{D}_{\text {train}}\) 上训练M个（实验中M=10 for ImageNet）epochs，更新网络权重 \(\Theta\) ：

\(\Theta=\underset{\Theta}{\operatorname{argmin}} \sum_{i=1}^{\mathbb{B}_{t}} \ell_{\operatorname{train}}\left(y_{i}, \mathcal{S}\left(x_{i}, \Theta, p\right)\right) \qquad (8)\)

在 \(\mathbb{D}_{\text {valid}}\) 上训练N个（实验中N=2 for ImageNet）epochs，更新结构参数 \(\alpha\) :

\(p=\underset{p}{\operatorname{argmin}} \sum_{i=1}^{\mathbb{B}_{v}} \ell_{v a l}\left(y_{i}, \mathcal{S}\left(x_{i}, \Theta, p\right)\right) \qquad (9)\)


image-20200803181007793

A2.s13 取出最佳子网fine-tune到收敛

训练到收敛，没有说具体的epochs


Experiments

CIFAR-10

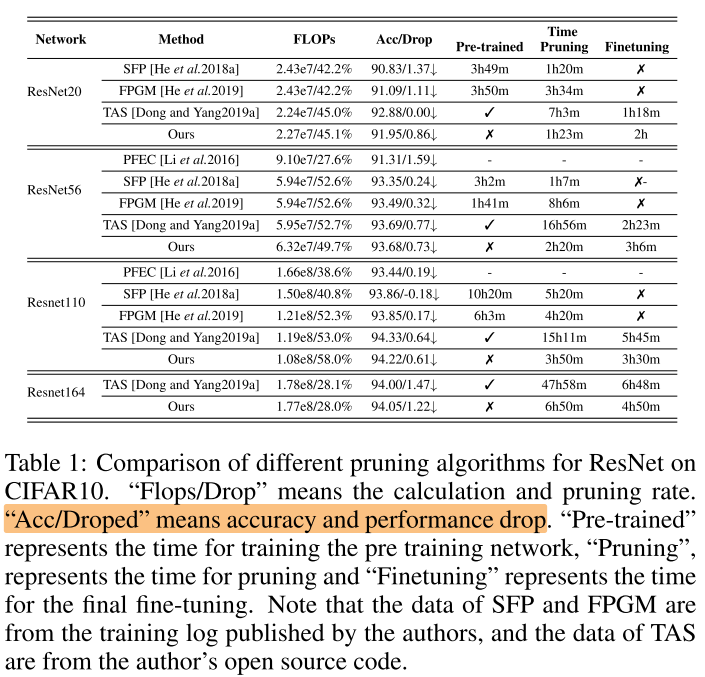
image-20200803193219534


CIFAR-100

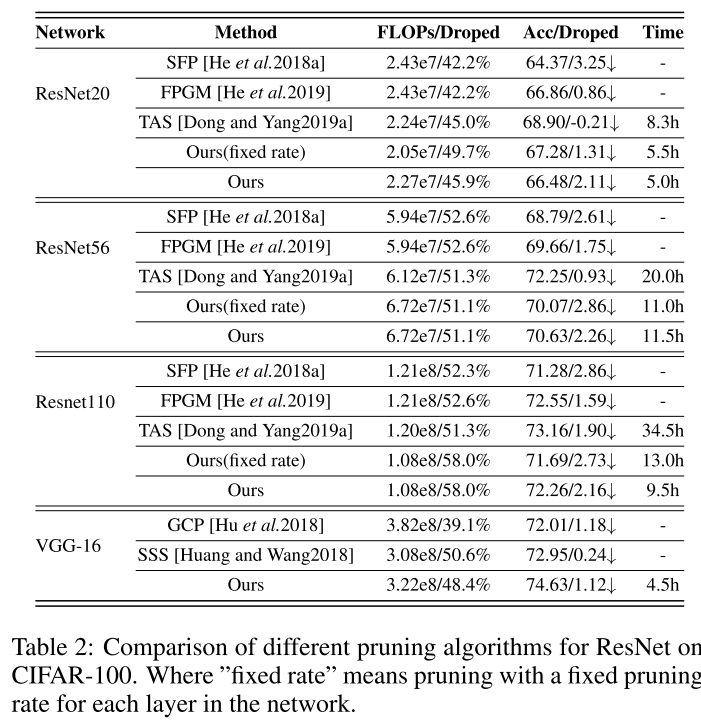
image-20200803193240867


ImageNet

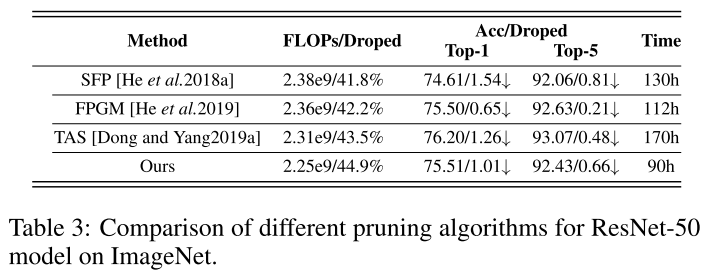
image-20200803193258930


Conclusion


Summary

  • 对比的都是比较早的文章？
  • 给每个filter赋予一个结构参数（表征该filter的重要性），不断从backbone网络中抽样（保留最重要的前k个filter）子网进行训练，迭代更新网络权重和结构参数（每个
  • 方法看起来很复杂，比如：
    • 在大网络中选取子网络不是用直观的概率抽样（nas中），也不是用全局的统一阈值（全局剪枝），而是用一个代理全连接网络 ThresNet 来预测每一层的阈值（这个阈值又不是直接小于阈值filter删除，而是累加最大的k个，直到达到阈值）
    • 使用全连接网络预测每一层的阈值，应该可以直接展开成一维，却要使用多级全连接层；还有sampler加的一些随机扰动等等，感觉为了复杂而复杂，不够简洁
  • 核心就是类似one-shot的在超网中抽样子网进行训练
  • 暂时没有开源

Reference


posted @ 2020-08-05 17:45  ChenBong  阅读(316)  评论(0)    收藏  举报