# Educational Codeforces Round 180 (Rated for Div. 2) 题解 A-E

Educational Codeforces Round 180 (Rated for Div. 2) 题解 A-E

目标：写（一堆废话） 详细的没有注意到和显然的题解

欢迎大家在评论区指出错误或说的不清楚的地方，或者分享被卡住的地方喵

A. Race

难度（个人感觉）：\(\star\)

猜答案是容易的，不过可能并不是很清晰。形式化一些可以看得更清楚。

不妨设 x < y

画出所有 (与 x 相差距离，与 y 相差距离) 的点
以 x = 3, y = 8 为例。

题目即询问， Alice 的点左下角存不存在其它点。
红线 (a < x) 与绿线 (a > y) 上点都符合，蓝线上的点不符合。

my submissioin

B. Shrinking Array

难度（个人感觉）：\(\star\star\)

先考虑如何从不满足转化为满足。

我们要将 \(a_i\) 和 \(a_{i+1}\) 变成一个中间值 \(mid\)。\(mid\) 与 \(a_{i-1}，a_{i+2}\) 的其中一个数 绝对值差不超过 1，我们考虑数组里什么样的三个数可以达到这种效果。

实际上，只要能变成绝对值差不超过 1，就一定变成能相等：

• 当三个数的中间值在左边或右边，即这是一个峰（中间的数是其中最大的或最小的），将另外两个数合并成中间值就行。

• 否则不存在峰，这三个数是单调的，操作后整个数组相邻数的差值不会变小，因此不可行。

吐槽：绝对值不超过 1 这个条件是没必要的，不自然的，会带来很多误导。

总之，这个数组有可能已经合法，否则若存在峰则有解且步数为 1，若不存在峰（即单调），则永远不能生成峰，所以无解。

my submissioin

C. Shrinking Array

难度（个人感觉）：\(\star\star\)

先排序。

设选 \(i < j < k\) , 那么 \(a[i] < a[j] < a[k] ①\)

为了防止 Bob 选其中的数，要求 \(a[k] < a[i] + a[j] ②\) 。

为了防止 Bob 选之外的数，要求 \(a[i] + a[j] + a[k] > max\{a\} ③\) 。

固定 i ， 从小到大枚举 j ，设 k 最小值为 l （初始为 N）， 最大值为 r （初始为 j） 。

对新的 j，

因为 j 变大了，所以为了保持 ①， l 与 \(j + 1\) 取 max 。

因为 \(a[j]\) 变大了，放宽了 ②，所以 r 在不越界和 ② 的限制下变大

因为 \(a[j]\) 变大了，放宽了 ③，所以 l 在大于 j 和 ③ 的限制下变小

之后加上答案 \(max(0, r - l + 1)\)。

my submissioin，我使用了左闭右开区间，即代码里 r 比文中 r 大 1。

D. Reachability and Tree

难度（个人感觉）：\(\star\star\star\)

路径数看起来有点困难，我们来分析这些路径的构成。首先每条边都是一条路径，有共同端点且方向相同的两条边是一条长度为 2 的路径。

那么 N 条边中，有 N - 1 条是长度为 1 的，剩下一条路径是长度为 2 的（更长会导致至少多两条边）。

直接构造比较困难（其实很简单），我们从答案推导做法，可以先把这两条边画出来。

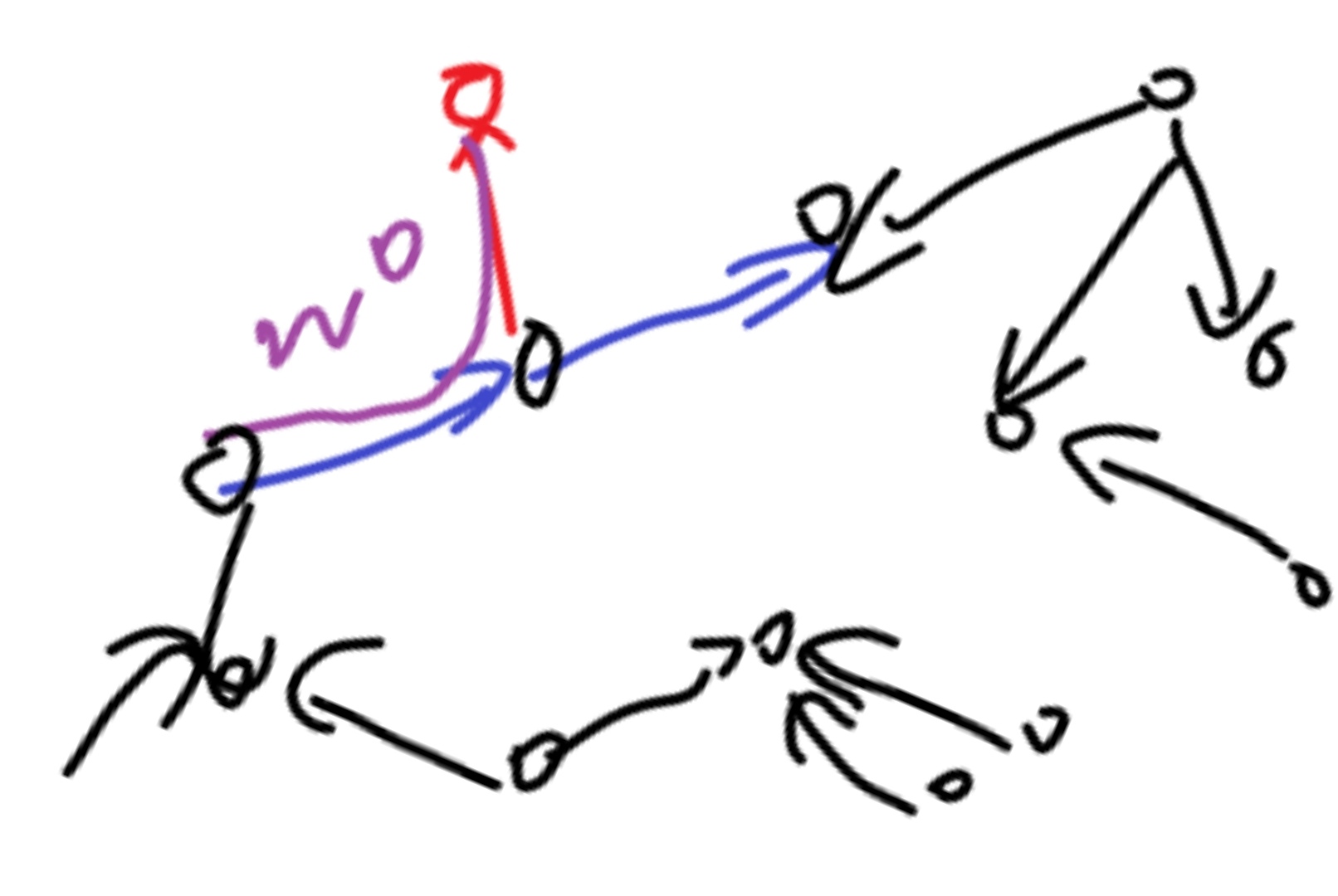
可以发现中间那个点之外不能继续延申，否则会和原始两条边之一形成路径。
而两个端点之外任何形态都可以。具体构造方法是以中间那个点为根，向外扩展。每个祖先到节点的边和节点到孩子的边都相反。

my submissioin

E. Tree Colorings

难度（个人感觉）：\(\star\star\star\)

首先看看着色方案数是多少。

首先一个点着黄必须子树全黄，否则违反第二条，即这个点的连通块把上面的连通块（因为根为绿色，所以存在）和下面的连通块（因为子树不全黄，所以存在）隔开了。
同理，蓝色的子树必须全蓝，否则违反第三条。

因为上面的选择会影响下面的，所以考虑分治。设树 T 的方案数是 way(T) 。对于一个确定的树，方案数是

\(\prod\limits_{v \in son_u} way(subtree(v)) + 2\)

这是因为，子树在原来的基础上，增加了全黄和全蓝两种方案。

这题的关键是没有限制，要（不可以重复）不遗漏的枚举所有形态。

那么朴素的想法是，当我们想知道方案数为 x 的树的最小节点数时，我们枚举每个子树的方案数分别是多少（要求上面的式子值为 x），得到这种情况下整个树的最小节点数（子树最小节点数之和 + 1（根节点）），取最小的节点数作为答案。

用 dp 优化一下就结束了。

具体来说，初始为根节点，方案数（作为键）为 1，最小节点数为 1。在原始已经有根节点和前几颗子树的基础上，不断加入一颗新的子树，方案数（这里作为键）乘上 \(way(this\;subtree) + 2\) ，最小节点数（作为值）增加这个子树的节点数。

这里比较怪异的事情是转移是 \(g[j] \rightarrow g[(i + 2) * j]\), 其中转移参赛 \(g[i]\) 是在过程中决定的。所以 i 只能从小到大枚举。

\(g ：way \rightarrow min\;size\)

g[1] = 1;
for(int i = 1; i <= MAX; i++){
  for(int j = 1; (i + 2) * j <= MAX; j++){
    chmin(g[(i + 2) * j], g[i] + g[j]);
  }
}

j 是原先的部分的方案数，i 是新加的子树的方案数。
这里是调和级数，时间复杂度 \(O(nlogn)\) 。

my submissioin