堆排序

堆排序

堆从根节点上是否比子节点的数值上更大从而分为大根堆和小根堆。
而从结构又分为，满二叉树和完全二叉树。
满二叉树是每个根节点都有两个子节点。
完全二叉树则是在最后一层从左到右依次存在节点，可以空缺。但是除了最后一层外，其余层都不能空缺。

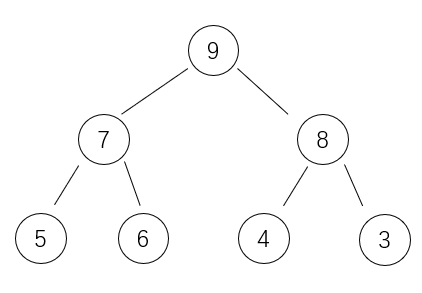
满二叉树（大根堆）

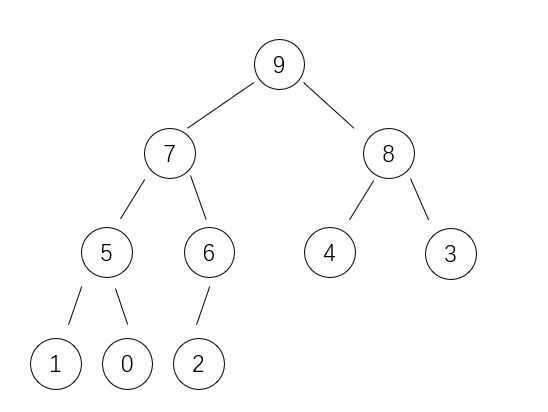
完全二叉树（最后一层可以有空缺，但是左边一定要依次填满）

建立堆

def sift(li, low, high):
    temp = li[low]
    i = low
    j = 2*i+1
    while j <= high:
        if j＋１ < high and li[j+1]>li[j]:
            j += 1
        if li[j] > temp:
            li[j], temp = temp, li[j]
            i = j
            j = 2 * i +1
        else:
            break
    else:
      li[i] = temp
def heap(li):
    n = len(li)
    # 1、建立堆
    for i in range((n-2)//2, -1, -1):  # 循环每一个小节点
        sift(li, i, n)                # 针对每一个小节点排序
    # 2、排序出数
    for i in range(n-1, -1, -1):    #　
        li[i], li[0] = li[0], li[i]
        sift(li, 0, i-1)