当那 光辉架构 分崩离析 围观者 满足了好奇 崇拜者 控诉着背弃 全世界只剩我陪伴你
test32
4-A 聚集 (gather.cpp)
匹配顺序排序显然,考虑滑动 \([l',r']\),向左右移动的字符是前后缀并且长度单调,双指针就好了。
#include<bits/stdc++.h>
#define int long long
#define up(i,l,r) for(int i=l; i<=r; ++i)
#define dn(i,r,l) for(int i=r; i>=l; --i)
using namespace std;
const int N=1000005, inf=1e13;
int n, m, p[N], pre[N], suf[N], Ans=inf;
char str[N];
int sum(int l,int r) { return (l+r)*(r-l+1)/2; }
signed main() {
// freopen("1.txt","r",stdin);
freopen("gather.in","r",stdin);
freopen("gather.out","w",stdout);
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n >> (str+1);
up(i,1,n) if(str[i]=='1') p[++m]=i;
up(i,1,m) pre[i]=pre[i-1]+p[i];
dn(i,m,1) suf[i]=suf[i+1]+p[i];
int j=1;
for(int l=1, r=m; r<=n; ++l, ++r) {
while(j<=m&&p[j]<=l+j-1) ++j;
// 1,...,j-1 ->,j,...,m <-
Ans=min(Ans,sum(l,l+j-2)-pre[j-1]+suf[j]-sum(l+j-1,r));
}
cout << Ans << '\n';
return 0;
}
4-B 火车 (train.cpp)
转移方式极度混乱无序,看着没办法简单、巧妙、polylog,那么考虑根号分治,\(x\leq B\) 的可以拿一个数组记录跳跃长度、余数一定的贡献,\(x>B\) 的暴力转移即可。
#define _CRT_SECURE_NO_WARNINGS
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#pragma GCC optimize("inline")
#pragma GCC optimize("-fgcse")
#pragma GCC optimize("-fgcse-lm")
#pragma GCC optimize("-fipa-sra")
#pragma GCC optimize("-ftree-pre")
#pragma GCC optimize("-ftree-vrp")
#pragma GCC optimize("-fpeephole2")
#pragma GCC optimize("-ffast-math")
#pragma GCC optimize("-fsched-spec")
#pragma GCC optimize("unroll-loops")
#pragma GCC optimize("-falign-jumps")
#pragma GCC optimize("-falign-loops")
#pragma GCC optimize("-falign-labels")
#pragma GCC optimize("-fdevirtualize")
#pragma GCC optimize("-fcaller-saves")
#pragma GCC optimize("-fcrossjumping")
#pragma GCC optimize("-fthread-jumps")
#pragma GCC optimize("-funroll-loops")
#pragma GCC optimize("-fwhole-program")
#pragma GCC optimize("-freorder-blocks")
#pragma GCC optimize("-fschedule-insns")
#pragma GCC optimize("inline-functions")
#pragma GCC optimize("-ftree-tail-merge")
#pragma GCC optimize("-fschedule-insns2")
#pragma GCC optimize("-fstrict-aliasing")
#pragma GCC optimize("-fstrict-overflow")
#pragma GCC optimize("-falign-functions")
#pragma GCC optimize("-fcse-skip-blocks")
#pragma GCC optimize("-fcse-follow-jumps")
#pragma GCC optimize("-fsched-interblock")
#pragma GCC optimize("-fpartial-inlining")
#pragma GCC optimize("no-stack-protector")
#pragma GCC optimize("-freorder-functions")
#pragma GCC optimize("-findirect-inlining")
#pragma GCC optimize("-fhoist-adjacent-loads")
#pragma GCC optimize("-frerun-cse-after-loop")
#pragma GCC optimize("inline-small-functions")
#pragma GCC optimize("-finline-small-functions")
#pragma GCC optimize("-ftree-switch-conversion")
#pragma GCC optimize("-foptimize-sibling-calls")
#pragma GCC optimize("-fexpensive-optimizations")
#pragma GCC optimize("-funsafe-loop-optimizations")
#pragma GCC optimize("inline-functions-called-once")
#pragma GCC optimize("-fdelete-null-pointer-checks")
#include<bits/stdc++.h>
#define int long long
#define up(i,l,r) for(int i=l; i<=r; ++i)
#define dn(i,r,l) for(int i=r; i>=l; --i)
#define pb push_back
using namespace std;
const int N=100005, M=320, P=1e9+7;
int n, B, g[M][M], d[N], x[N], f[N], Ans;
vector<int> del[N];
inline void add(int &a,int b) { a=(a+b)%P; }
signed main() {
freopen("train.in","r",stdin);
freopen("train.out","w",stdout);
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n, B=sqrt(n);
up(i,1,n) cin >> d[i] >> x[i];
f[1]=1;
up(i,1,n) {
up(j,1,B) add(f[i],g[j][i%j]);
add(Ans,f[i]);
// cout << "check " << i << " = " << f[i] << '\n';
if(d[i]) {
if(d[i]<=B) {
add(g[d[i]][i%d[i]],f[i]);
if(i+d[i]*x[i]<=n) del[i+d[i]*x[i]].pb(i);
}
else {
int j=i;
up(u,1,x[i]) {
j+=d[i];
if(j>n) break;
add(f[j],f[i]);
}
}
}
for(int j:del[i]) add(g[d[j]][j%d[j]],-f[j]);
}
cout << (Ans%P+P)%P << '\n';
return 0;
}
4-C 海战 (navy.cpp)
首先可以完全独立地分类讨论 6 种相撞方式,讨论出来放进优先队列里面比较得了,就是注意延迟删除(或者说 \(T\) 一致地一起删除)。赶着早退就只简略说一种情况了,能相撞的船肯定在同一条斜线上,那么只要保证斜线上相邻不同的那些点对被塞进优先队列里面就行了,用 set 动态维护即可,想要卡常也可以排序+双向链表但是本可没有那个心情 /wq
#define _CRT_SECURE_NO_WARNINGS
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#pragma GCC optimize("Ofast")
#pragma GCC optimize("inline")
#pragma GCC optimize("-fgcse")
#pragma GCC optimize("-fgcse-lm")
#pragma GCC optimize("-fipa-sra")
#pragma GCC optimize("-ftree-pre")
#pragma GCC optimize("-ftree-vrp")
#pragma GCC optimize("-fpeephole2")
#pragma GCC optimize("-ffast-math")
#pragma GCC optimize("-fsched-spec")
#pragma GCC optimize("unroll-loops")
#pragma GCC optimize("-falign-jumps")
#pragma GCC optimize("-falign-loops")
#pragma GCC optimize("-falign-labels")
#pragma GCC optimize("-fdevirtualize")
#pragma GCC optimize("-fcaller-saves")
#pragma GCC optimize("-fcrossjumping")
#pragma GCC optimize("-fthread-jumps")
#pragma GCC optimize("-funroll-loops")
#pragma GCC optimize("-fwhole-program")
#pragma GCC optimize("-freorder-blocks")
#pragma GCC optimize("-fschedule-insns")
#pragma GCC optimize("inline-functions")
#pragma GCC optimize("-ftree-tail-merge")
#pragma GCC optimize("-fschedule-insns2")
#pragma GCC optimize("-fstrict-aliasing")
#pragma GCC optimize("-fstrict-overflow")
#pragma GCC optimize("-falign-functions")
#pragma GCC optimize("-fcse-skip-blocks")
#pragma GCC optimize("-fcse-follow-jumps")
#pragma GCC optimize("-fsched-interblock")
#pragma GCC optimize("-fpartial-inlining")
#pragma GCC optimize("no-stack-protector")
#pragma GCC optimize("-freorder-functions")
#pragma GCC optimize("-findirect-inlining")
#pragma GCC optimize("-fhoist-adjacent-loads")
#pragma GCC optimize("-frerun-cse-after-loop")
#pragma GCC optimize("inline-small-functions")
#pragma GCC optimize("-finline-small-functions")
#pragma GCC optimize("-ftree-switch-conversion")
#pragma GCC optimize("-foptimize-sibling-calls")
#pragma GCC optimize("-fexpensive-optimizations")
#pragma GCC optimize("-funsafe-loop-optimizations")
#pragma GCC optimize("inline-functions-called-once")
#pragma GCC optimize("-fdelete-null-pointer-checks")
#include<bits/stdc++.h>
#define up(i,l,r) for(int i=l; i<=r; ++i)
#define dn(i,r,l) for(int i=r; i>=l; --i)
#define pii pair<int,int>
#define mp make_pair
#define pb push_back
using namespace std;
const int N=600005;
int n, tot, x[N], y[N], tag[N], Ans;
char opt[N];
map<pii,int> id;
set<pii> pos[N];
struct node {
int i, j, w;
bool operator<(const node &rhs) const { return w>rhs.w; }
}; priority_queue<node> q;
void remove(int i) {
if(opt[i]=='N'||opt[i]=='E') {
int u=id[mp(1,x[i]-y[i])];
pos[u].erase(mp(x[i],i));
if(pos[u].size()>1) {
auto R=pos[u].lower_bound(mp(x[i],i)), L=R;
if(R!=pos[u].end()&&L!=pos[u].begin()) {
int l=(*--L).second, r=(*R).second;
if(opt[l]=='E'&&opt[r]=='N') q.push((node){l,r,x[r]-x[l]});
}
}
}
if(opt[i]=='N'||opt[i]=='S') {
int u=id[mp(2,x[i])];
pos[u].erase(mp(y[i]/2,i));
if(pos[u].size()>1) {
auto R=pos[u].lower_bound(mp(y[i]/2,i)), L=R;
if(R!=pos[u].end()&&L!=pos[u].begin()) {
int l=(*--L).second, r=(*R).second;
if(opt[l]=='S'&&opt[r]=='N') q.push((node){l,r,(y[r]-y[l])/2});
}
}
}
if(opt[i]=='N'||opt[i]=='W') {
int u=id[mp(3,x[i]+y[i])];
pos[u].erase(mp(x[i],i));
if(pos[u].size()>1) {
auto R=pos[u].lower_bound(mp(x[i],i)), L=R;
if(R!=pos[u].end()&&L!=pos[u].begin()) {
int l=(*--L).second, r=(*R).second;
if(opt[l]=='N'&&opt[r]=='W') q.push((node){l,r,x[r]-x[l]});
}
}
}
if(opt[i]=='E'||opt[i]=='S') {
int u=id[mp(4,x[i]+y[i])];
pos[u].erase(mp(x[i],i));
if(pos[u].size()>1) {
auto R=pos[u].lower_bound(mp(x[i],i)), L=R;
if(R!=pos[u].end()&&L!=pos[u].begin()) {
int l=(*--L).second, r=(*R).second;
if(opt[l]=='E'&&opt[r]=='S') q.push((node){l,r,x[r]-x[l]});
}
}
}
if(opt[i]=='E'||opt[i]=='W') {
int u=id[mp(5,y[i])];
pos[u].erase(mp(x[i]/2,i));
if(pos[u].size()>1) {
auto R=pos[u].lower_bound(mp(x[i]/2,i)), L=R;
if(R!=pos[u].end()&&L!=pos[u].begin()) {
int l=(*--L).second, r=(*R).second;
if(opt[l]=='E'&&opt[r]=='W') q.push((node){l,r,(x[r]-x[l])/2});
}
}
}
if(opt[i]=='S'||opt[i]=='W') {
int u=id[mp(6,x[i]-y[i])];
pos[u].erase(mp(x[i],i));
if(pos[u].size()>1) {
auto R=pos[u].lower_bound(mp(x[i],i)), L=R;
if(R!=pos[u].end()&&L!=pos[u].begin()) {
int l=(*--L).second, r=(*R).second;
if(opt[l]=='S'&&opt[r]=='W') q.push((node){l,r,x[r]-x[l]});
}
}
}
}
signed main() {
freopen("navy.in","r",stdin);
freopen("navy.out","w",stdout);
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n;
up(i,1,n) cin >> x[i] >> y[i] >> opt[i];
up(i,1,n) {
if(opt[i]=='N'||opt[i]=='E') {
int val=x[i]-y[i];
if(!id[mp(1,val)]) id[mp(1,val)]=++tot;
pos[id[mp(1,val)]].insert(mp(x[i],i));
}
if(opt[i]=='N'||opt[i]=='S') {
int val=x[i];
if(!id[mp(2,val)]) id[mp(2,val)]=++tot;
pos[id[mp(2,val)]].insert(mp(y[i]/2,i));
}
if(opt[i]=='N'||opt[i]=='W') {
int val=x[i]+y[i];
if(!id[mp(3,val)]) id[mp(3,val)]=++tot;
pos[id[mp(3,val)]].insert(mp(x[i],i));
}
if(opt[i]=='E'||opt[i]=='S') {
int val=x[i]+y[i];
if(!id[mp(4,val)]) id[mp(4,val)]=++tot;
pos[id[mp(4,val)]].insert(mp(x[i],i));
}
if(opt[i]=='E'||opt[i]=='W') {
int val=y[i];
if(!id[mp(5,val)]) id[mp(5,val)]=++tot;
pos[id[mp(5,val)]].insert(mp(x[i]/2,i));
}
if(opt[i]=='S'||opt[i]=='W') {
int val=x[i]-y[i];
if(!id[mp(6,val)]) id[mp(6,val)]=++tot;
pos[id[mp(6,val)]].insert(mp(x[i],i));
}
}
up(u,1,tot) {
int j=0, y;
for(pii sav:pos[u]) {
int i=sav.second, x=sav.first;
if(j&&opt[i]!=opt[j]) {
if(opt[j]=='E'&&opt[i]=='N'
||opt[j]=='S'&&opt[i]=='N'
||opt[j]=='N'&&opt[i]=='W'
||opt[j]=='E'&&opt[i]=='S'
||opt[j]=='E'&&opt[i]=='W'
||opt[j]=='S'&&opt[i]=='W') {
q.push((node){i,j,x-y});
}
}
j=i, y=x;
}
}
int pre=0; vector<int> del;
while(q.size()) {
int i=q.top().i, j=q.top().j, t=q.top().w; q.pop();
if(t>pre) { pre=t; for(int u:del) tag[u]=1; del.clear(); }
if(tag[i]||tag[j]) continue;
remove(i), del.pb(i), remove(j), del.pb(j);
}
for(int u:del) tag[u]=1;
up(i,1,n) if(!tag[i]) cout << i << '\n';
return 0;
}
4-D 城市 (city.cpp)
首先对于边 \(i\),肯定会选择更美丽的道路中权值最大的边复制,即 \(\Delta_i=\max_{j>i}\{w_j\}\)。问题变成对每一个 \(i\in [1,m)\) 求出 \(w_i\to w_i+\Delta_i\) 后 \(1\to n\) 的最短路,分类讨论取 \(\min\) 就是新的最短路,如果经过这条边最短路变为 \(f_n+\Delta_i\),所以我们还要额外求出删除原 \(1\to n\) 最短路经上的边 \(e_1,\dots,e_m\) 后的最短路分别是多少。
不妨在最短路形成的 DAG 上考虑问题,特别的权为 \(0\) 的边按照计算最短路时的拓展序定向(原图上处理最短路的时候我们可以将 \(0\) 权边和连通的点视作一个整体,联通块对外的顺序是一定的,而拓展序符合这个关系)。现在考虑删除某一条边 \(e\) 的影响,首先如果 \(1\to n\) 的最短路不一定要经过 \(e\),那么答案不会变化。
所以我们进一步考虑 \(e\) 是最短路 DAG 的割边的情况,我们会选择 DAG 前半部分的 \(i\) 和后半部分的 \(j\),用一些在 DAG 外的边将其连接 \(i\to o_1\to ...\to o_t\to j\),绿边都是非 DAG 边,注意到 \(o\) 的前/后缀应该在 DAG 的前/后半部分不然肯定不是最短路,所以只要 \(o\) 上跨越前后缀的那一条非 DAG 边就足够了,别的直接用 DAG 边就不劣了。
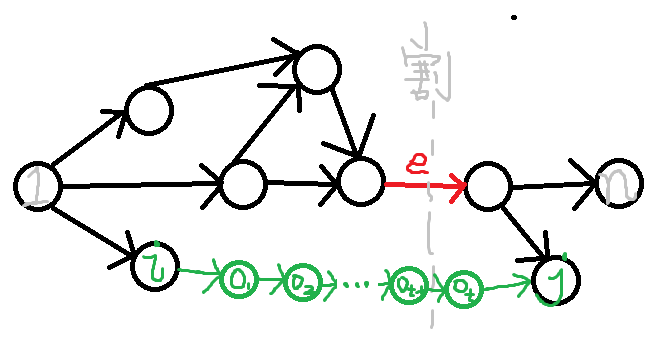
我们现在要想办法划分开前后缀的点集分别是什么(要在实际上需要划分的时候划分正确),顺便维护跨越的非树边 \(\{(u,v)\}\) 集合是什么、最小路径长度是什么。首先快速对 \((u,v)\) 求出答案可以预处理出反图的最短路 \(g\),答案就是 \(f_u+g_v+w(u\to v)\),维护边集只依赖点集划分的信息、而划分点集只要连通性充分就行了,所以不妨考虑随便来一棵 DAG 的生成树(比如说 dij 转移关系),当然也可以但我不建议写诡异到极点的另类拓扑排序(?),这样子非 DAG 边贡献给哪些 \(e\) 就很明了是 \(1\to n\) 路径的一个区间来的,类似差分把贡献打上去、用 multiset 求 rmq 即可。还有就是要让这个做法适应于 \(e\) 不是割边的情况,显然是把 DAG 上的非树边也扔进去贡献就好了。
实现的话可以 dij 的时候记录 \(f_u\) 从 \(fa_u\) 转移,然后写并查集,\(1\to n\) 的路径为并查集的祖先,别的点向 \(fa_u\) 合并,对于顺着 DAG 的可能贡献的边,并查集快速找到区间。还有什么别的可以去看 alenchoi 大神的题解。
#include<bits/stdc++.h>
#define int long long
#define up(i,l,r) for(int i=l; i<=r; ++i)
#define dn(i,r,l) for(int i=r; i>=l; --i)
#define pii pair<int,int>
#define mp make_pair
#define pb push_back
using namespace std;
const int N=300005, inf=1e18;
int n, m, tot, tag[N], dis[N], g[N], fa[N], Ans, dsu[N], val[N];
vector<pii> to[N];
vector<int> add[N], del[N];
map<pii,int> id;
priority_queue<pii,vector<pii>,greater<pii> > q;
multiset<int> qwq;
int get(int x) { return x==dsu[x]?x:dsu[x]=get(dsu[x]); }
signed main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n >> m;
up(i,1,m) {
int u, v, w;
cin >> u >> v >> w;
to[u].pb(mp(v,w));
to[v].pb(mp(u,w));
id[mp(u,v)]=id[mp(v,u)]=i;
val[i]=w;
}
dn(i,m,1) val[i]=max(val[i],val[i+1]);
up(i,2,n) dis[i]=inf;
q.push(mp(0,1));
while(q.size()) {
int x=q.top().second; q.pop();
if(tag[x]) continue;
tag[x]=1;
for(pii sav:to[x]) {
int y=sav.first, w=sav.second;
if(dis[x]+w<dis[y]) {
fa[y]=x, dis[y]=dis[x]+w;
q.push(mp(dis[y],y));
}
}
}
up(i,1,n) tag[i]=0, g[i]=inf;
g[n]=0, q.push(mp(0,n));
while(q.size()) {
int x=q.top().second; q.pop();
if(tag[x]) continue;
tag[x]=1;
for(pii sav:to[x]) {
int y=sav.first, w=sav.second;
if(g[x]+w<g[y]) {
g[y]=g[x]+w;
q.push(mp(g[y],y));
}
}
}
up(i,1,n) tag[i]=0;
for(int i=n; i; i=fa[i]) tag[i]=-(++tot);
up(i,1,n) dsu[i]=tag[i]?i:fa[i];
up(x,1,n) for(pii sav:to[x]) {
int y=sav.first, w=sav.second;
int xx=get(x), yy=get(y);
if(tag[xx]>=tag[yy]) continue;
if(tag[xx]+1==tag[yy]&&x==xx&&y==yy) continue;
int len=dis[x]+w+g[y];
add[yy].pb(len), del[xx].pb(len);
}
Ans=dis[n];
for(int i=n; i!=1; i=fa[i]) {
for(int v:add[i]) qwq.insert(v);
for(int v:del[i]) qwq.erase(qwq.find(v));
if(id[mp(i,fa[i])]<m) {
int ran=dis[n]+val[id[mp(i,fa[i])]+1];
if(qwq.size()) ran=min(ran,*qwq.begin());
Ans=max(Ans,ran);
}
}
cout << Ans << '\n';
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号