口胡赛 2025.2.5

link 喵 >_<

---

T1

首先不要 \(p\) 这个肯定是不能枚举 \(p\) 再直白处理的，因为最快的 Floyd 都要 \(O(n^3)\) 这样。

那么不要 \(p\) 的信息是合并得来的，但是直接合并复杂度也不够，考虑使用经典分治，先加入 \([l,mid]\) 然后递归 \((mid,r]\)，撤销 \([l,mid]\)，加入 \((mid,r]\)，在递归 \([l,mid]\)，这样子分治复杂度 \(O(n\log n)\)，加上加入的复杂度就是 \(O(n^3\log n)\)。

---

T2

首先出度最大的点 \(x\) 肯定满足条件，\(x\to S\)，\(T\to x\)，如果存在 \(S\to T\) 那么一定满足条件，所以不满足时一定有 \(T\to S\)，那么此时 \(T\) 中某点的出度更大，因为在有 \(|S|\) 的基础上多了 \(T\to x\) 的红边。

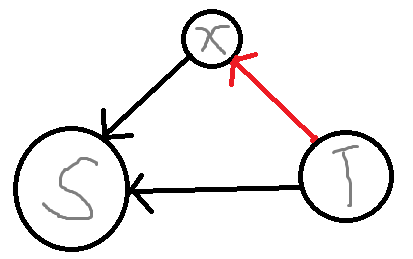
如果此时 \(T\) 为空，那说明这个图根本就无解嘛，因为 \(x\) 只有外向边。注意到 \(T\) 中的点可以通过 \(x\) 很快到达 \(S\)，那么第二个点只用考虑 \(T\) 这个子问题，求出 \(T\) 中出度最大的点 \(y\) 即可。

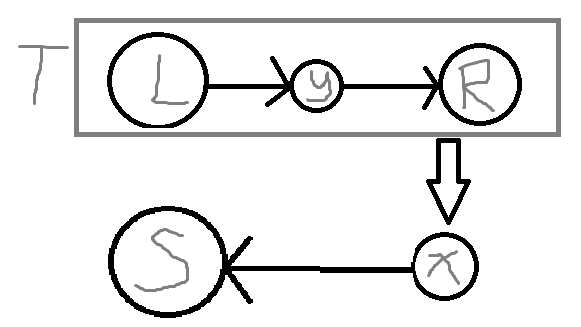
之后会变成如图所示的东西，如果 \(L\) 里面有东西那就同理递归子问题，如果 \(L\) 里面没有东西，我们再讨论。

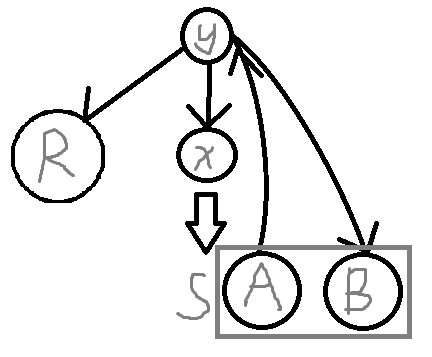
假设 \(S\) 没有到 \(y\) 的边那么无解，不然考虑 \(S\) 到 \(y\) 的点集 \(A\)，别的为 \(B\)，那么 \(A\to y\to x/R/B\)，在 \(A\) 里面做子问题即可。

---

T3

题目保证所有树有根，\(|A|,|B|\geq 2\)

先考虑 \(AX=C\) 怎么做，可以做一个树哈希，或者找到最深的点向上找到大小恰好为 \(\frac{|C|}{|A|}\) 的子树。

现在的问题主要是怎么区分 \(C\) 的子树成分，最大的子树一定是 \(maxsiz(sonA)\times |X|\) 或者 \(maxsiz(sonB)\times |Y|\)，不妨假定是前者，那么 \(X\) 就很好解出来了，现在考虑做 \(C-AX\) 得到 \(BY\)，这样子就很好解 \(Y\) 了。减法就暴力算出 \(AX\) 的每一颗子树，哈希匹配，暴力删去即可。

---

T4

首先看到这个 \(b_i\neq c_i\) 关心数字，那么乘上 \(\prod cnt(num)!\) 变成更好算的排列答案。

然后就变成了 AT_arc148_e，这个题目让人印象挺深刻的其实。

---

T5

困难题我还是不做了。

---

T6

我们从小到大考虑 \(i\) 可以成为那些 \(j\) 的 \(b_j\)，因为已经考虑了 \(b_j=0,\dots,i-1\) 的，那么剩下的 \(j\) 的区间 \(\text{mex}\) 集合里面一定有 \([0,i)\)，现在只用考虑存不存在 \(i\)。

现在我们想知道对于有没有长度为 \(j\) 包含 \([1,i)\) 的区间有没有 \(i\)，对于 \([l,r]:len,[1,v]:value\) 来说这是一个矩形的问题，考虑扫描线。用线段树维护对于每一个左端点想要包含 \([1,i]\) 右端点最小是多少，这个显然单调递增。现在考虑从 \(i-1\) 扫到 \(i\)，考虑 \(a_i=i\) 的位置带来的影响，是一个区间取 \(\max\)，线段树可以维护。然后一个单点修改影响区间对答案的贡献是 \(j\in[\min,fix)\) 的答案不为 \(i\)，所以对这个取并的补就是没确定的 \(j\) 中答案可以为 \(i\) 的母集，这部分暴力 + set 可以搞（其实应该说啥都能搞。