2024.9 做题记录 / 享受此刻虚伪 渴望被充实包围

AT_agc005_e

不会这个题目的去玩几把第五人格还不会可以再来几把然后就会了。

首先回头走不优，实在要停，如果非要停这等死最后再停不劣，A 牵制 B 大致有一下方式：

• 往离 B 远的地方走加长 B 的走路时间。

• 找到一个位置，可以一直跟 B 绕无限久，此时答案就是 \(-1\)，我们称可以一直绕的地方为无敌点。

我们先考虑怎么判定一个无敌点，我们手玩答案为 \(-1\) 的样例，发现无敌点形式是，对于树 B 上的简单路径 \(p_1\to\dots\to p_x(x\geq 4)\)，A 有一条 \((p_1,p_x)\) 这样的边，如此一来，只要通过这条边一直靠在离 B 远的点就永远不会被抓到了 w

我们考虑树 A 的边的对应点对 \(u,v\) 在树 B 上的距离，如果 \(距离\geq 3\)，那么 \(u,v\) 是无敌点，我们处理出 B 那棵树以 \(y\) 为根时（只是算无敌点的话根不是 \(y\) 也行）每个点的深度 \(g[]\)，判定的话，不妨设 \(g[u]\leq g[v]\)，分类讨论可得如果满足\(fa[v]=u,fa[fa[v]]=u,fa[u]=fa[v]\) 其中之一那么这个边没有无敌点的贡献。

然后考虑 A 有没有命活到点 \(i\)，需要 \(x\to pre(i)\) 上的点都有命到达，以及 \(i\) 也要有命到达，设 \(f[i]\) 表示 A 上 \(x\to i\) 的距离，然后 \(i\) 额外的条件感觉是一个 \(f[x]<g[x]\)，但是这样有一个问题，比如有两条路径 \(\alpha,\beta\) 分别可以被 B 阻止，可以保证 B 能同时挡下来嘛，是可以的，无敌点不需要继续拉点，于是 A 拉点的边在 B 连接的一定是距离为 \(1\) 或 \(2\) 的点，又因为 A 不能跳到 B 或者 B 相邻的位置，所以 A 一直会在树 B 以 B 为根的包含 A 的子树里面跳不出去，B 会一直往包含 A 的子树里面走，这样追捕关系是清晰的。

---

P10614

普通的 LCS 直接 dp 就可以了，设计 \(f[i][j]\) 表示 \(|LCS(S[0,\dots,i-1],T[0,\dots,j-1])|\)，转移显然是 \(f[i][j]=\max\{f[i-1][j],f[i][j-1],f[i-1][j-1]+[S_i=T_j]\}\)。

题目中的 \(T\) 不确定我们直接写进状态里面，设计状态 \(f[i][str]\) 表示 \(|LCS(S[0,\dots,i-1],str)|\)，以 \(|str|\) 为轮是容易转移的。这个第二维过于大了，不过所有的 \(f[i][str]\) 都非常小，我们想办法把 \(str\) 的个数换成 dp 的答案，\(LCS\) 长度换成 dp 的状态。

不可以很直白的直接换，因为对于一个串，这个位置此时最优不代表一直会最优，小的位置可能会转移出更大的答案，不妨把 \(f[0,\dots,n-1][str]\) 看成一个整体，设计 \(f[i][O]\) 表示 \(|str|=i\) 且与 \(S[0],S[0,1],S[0,1,2],\dots,S[0,\dots,n-1]\) 的 \(|LCS|\) 集合为 \(O\) 的答案，注意到 \(O\) 相邻两位差不超过 \(1\)，所以可以二进制存这个集合的差分，转移向后刷表是平凡的，空间优化可以加个滚动，具体而言对于一个差分 \(O\)，我们还原其前缀和为 \(d[]\)，枚举新加入一个字符 \(c=A/T/C/G\)，要求新的答案数组 \(d'[]\)，初始化 \(d'[]=d[]\)，对于 \(c=S_i\) 有 \(d'[i]=\max(d'[i],d'[i-1]+1)\)，最后前缀弄一下一下 \(d'[i]=\max(d'[i-1],d'[i])\)，把 \(d'\) 弄成二进制状态 \(N\)，然后 \(f[nxt][N]\) 可以获得一个 \(f[now][O]\) 的加法贡献。最后对每一种差分把答案累加进去就可以得出了。

---

P4590

跟上面一题几乎一样，不能有连续字串就额外一维表示 \(T\) 的末尾跟 NOI 的匹配长度即可，转移也是简单的。

---

P2371

首先不难想到对 \(\mod a_i\) 做一个同余最短路，然后就水灵灵做完了。

---

AT_arc044_b

手玩一下不难发现距离为 \(x\) 的点可以且仅可以和距离为 \(x+1\) 的点连边，按照这个计数即可，注意特判 \(a_i=0\) 的 \(i\) 只能有 \(i=1\) 一个。

---

P7897

先考虑朴素一点的 dp，假设现在的增量为 \(\Delta\)，设 \(f[x]\) 表示 \(x\) 处的答案，显然有 \(f[x]=(a_x+\Delta)+\sum \max(f[y],0)\) 这样子，瓶颈是要做 \(\max(f[i],0)\)，我们称呼 \(f[x]<0\) 的点为黑点，黑点的存在会清空这个子树对其父亲的贡献，于是我们维护黑点为根且白点向原来的父亲连边这种形式的森林的答案，具体而言我们需要维护每个点 \(i\) 在树上的子树大小和子树权值和 \(siz[i]\) 和 \(val[i]\)。

不难想到离线使得 \(\Delta\uparrow\)，这样子只会有黑点变成白点，好处有变化总次数为 \(O(n)\) 且只用做树合并。现在我们需要考虑的就是怎么快速查找要变色的点，怎么快速合并树。

对于一棵树，根的 \(f\) 要求就是 \(siz\times \Delta+val\geq 0\)，也就是 \(\Delta\geq \lceil\frac{-val}{siz}\rceil\)，把这个时间塞进优先队列里面就行了呗。

考虑把树 \(x\) 向上合并进树 \(y\)（快速找父亲捏一个 dsu），发现是对 \(fa(x)\to y\) 这条链上的任意 \(i\) 有一个 \(siz[i]\) 变大 \(siz[x]\)，\(val[i]\) 变大 \(val[x]\) 这样的影响，是一个树上链加，直接 dfs 序 + 差分 + 树状数组维护即可。

---

P9755

先二分一个 \(limit\) 问题变成了判断可不可以在 \(limit\) 天内完成任务，有了这个上界之后可以对每一个点 \(x\) 求出 \(t[x]\) 表示为了完成任务要在 \(\leq t[x]\) 的时刻完成任务，\(t[x]\) 为了方便可以二分一个 \(\alpha\) 然后求 \(f_i\) 在 \([\alpha,limit]\) 的增量，差分变成求 \(f_i\) 的一个前缀到 \(e\) 的和，我们分类讨论，若 \(c_i\geq 0\)，直接等差数列求和即可，若 \(c_i<0\)，考虑函数 \([1,pos]\) 的部分是 \(f_i(o)=c_i\times o+b_i\)，\([pos+1,\infty]\) 的部分是 \(f_i(o)=1\)，首先 \(c_i\times pos+b_i\geq 1\)，得到 \(pos\gets \lfloor\frac{1-b_i}{c_i}\rfloor\)，如果 \(e\leq pos\)，等差数列求和，如果 \(e>pos\)，等差数列求和再加上 \(e-pos\) 即可。

现在变成了能不能保证到达每个点的时间都小于等于其 \(t\)，考虑贪心每次去打通到 \(t[i]\) 最小的 \(i\) 的路径，不难发现这样子不劣。

---

P8866

Ad-hoc 标签的题目写了绝美 128 行，也是激战半个晚修大半个早上。

不从部分分开始做显然不太实际，我们先看 \(k=2\times (n-1)\)，引导我们把 \(2\times t-1,2\times t\) 分配进栈 \(t\)，然后剩下一个辅助栈。不难想到策略：对于同一栈的 \(x,y\)，相邻出现的 \(xx/yy\) 现在对应栈中消除，对于剩下的 \(xy\) 交替的放入对应栈和辅助栈中。这个策略是容易人话表达的，如果当前加入的 \(x\) 在栈里，直接消去或者利用辅助栈消去，不然直接塞入分配栈，人话表达之后不难发现栈的长度永远 \(\leq 2\)。

我们再看 \(n=2,k=2\times 2-1=3\)，此时无法沿用上面的策略，比如说序列 123123，如果编号分配栈的话一定会有数被封印在栈底，想要消除这个序列只能用会破坏上面那种编号对应栈规则的类似 12/.->123/.->123/1->23/. 这种办法，我们手动把这个分讨出来：

• 如果加入可以保持 xy/.,x/. 甚至 . 的结构，我们直接做相消。

• 如果出现 xy/. 硬要加入一个 \(o\)，硬加之后只能选择栈顶相消，那对于在栈顶的就一直消呗。硬变成的 xy/o 的：如果加入 \(o\) 可以消出空栈作为辅助栈，这要求加入序列中这两个 \(o\) 之间的数全都是栈顶；如果消去 \(y\) 再消去 \(x\) 可以消出空栈作为辅助栈，这要求加入序列中 \(o\) 和 \(x\) 之间的数全都是栈顶且有奇数个 \(y\)。硬变成 \(xyo/.\) 的话：可以加入 \(o\) 消去，要求加入序列中这两个 \(o\) 之间的数全都是栈顶且不能有 \(y\)（所以其实不如把 \(o\) 放进辅助栈）；用辅助栈把 \(x\) 消掉也可以消出空栈作为辅助栈，这要求加入序列中 \(o\) 和 \(x\) 之间只能有栈顶，特别的可以有 \(y\) 但是必须是偶数个。

总结一下就是，找到 \(o\) 后面第一个栈底的数 \(x\) 或者 \(o\)，如果是 \(o\) 直接消去，如果是 \(x\)：中间有奇数个 \(y\)，把 \(o\) 放进辅助栈 \(y\) 会自然消去，最后消去 \(x\)，更新辅助栈；中间有偶数个 \(y\)，把 \(o\) 放进 \(xy\) 栈，\(y\) 在辅助栈中会自然消去，最后用空的辅助栈把 \(x\) 消去。

对于 \(n\) 更大的情况，先尽量保持结构直接做（有就消去没有就加入，保持有辅助栈且非辅助栈长度 \(\leq 2\)），是在不行就是什么数都必须有一个的情况了，往后遍历操作序列，平凡栈顶数不太影响其实，对于第一个出现的栈底数或者 \(o\)，拿出那个栈和辅助栈做 \(n=3\) 的讨论即可，然后就做完了.....？

---

CF516D

先求出直径的端点 \(L,R\)，考虑点到 \(L/R\) 的距离为 \(f[]/g[]\)，显然有 \(dis[x]=\max(f[x],f[y])\)。

原本的题目是一个线段树分治的板子，但是题目有性质，考虑以 \(dis[i]\) 最小的 \(i\) 作为根，这显然是一个小根堆，我们将 \(dis\) 的定义修改为点到根的距离，现在要求每一个子树中到子树根距离 \(\leq l\) 的点数。

考虑一个点 \(x\) 对哪些根 \(y\) 贡献，应该满足 \(dis[x]-dis[y]\leq l\) 即 \(dis[y]\geq dis[x]-l\)，直接在搜索栈上二分然后树上差分一个 \(tag\) 就做完了。

---

CF1442E

先考虑没有灰色心情的情况，先把 黑/白 联通块缩在一起变成二分图，手玩发现答案只跟直径长度相关。

我们考虑 dp 直径长度的同时的时候最小化 dp 值，设 \(f[x]\) 表示离 \(x\) 最远距离是多少，设 \(sum[y]=f[y]-[col_x\neq col_y]\)，那么 \(f[x]=\max\{sum[y]\}+1\)，同时会有一条长度为 \(\max_{y_1\neq y_2}\{sum[y_1]+sum[y_2]+1\}\) 的路径可能成为直径。

在权不定（\(0/1/-1\)）的情况下做分类讨论就显得有点麻烦了（应该是我比较笨 wa 了），直接上一个有脑二分，黑白点直接 dp，灰色心情按照黑点白点分别 dp，在满足贡献路径合法的情况下最小化 \(f[x]\)，如果什么颜色 \(f[x]\) 都最小那就保持灰色心情，然后就做完了。

---

CF1038F

我们考虑在 ac 自动机上 dp，我们枚举 \(st=0,\dots,m\)，表示后半个串从 ac 机上哪个点开始转移，\(st\) 不同的串肯定是不同的。

设计 \(f[t][i][j][0/1]\) 表示目前构建了长度为 \(t\) 的串，前/后半部分在 ac 机上的位置为 \(i/j\)，目前有/没有碰到重点 的情况的方案数，转移是一个比较显然的向后刷表，\(Ans=\sum f[n][st][][1]\)。

---

AT_agc026_d

考虑一个类似笛卡尔树的 dp 顺序，先确定下面那个公有的大矩形然后递归处理问题。\([l,r]\) 中 \(\Delta\) 以下的部分已经被钦定了（\(\Delta\) 是 \(h_{fa(p)}\) 这种东西）且对上面的染色没有影响，设这个方案数为 \(f(l,r,\Delta)\)，假设 \(p\) 是区间 \([l,r]\) 中严格最矮的且 \(\Delta<h_p\)（如果没有就递归到有）。我们先钦定 \(p\) 这一列高度为 \((\Delta,h_p]\) 的格子的颜色，然后考虑 \([l,r]\) 中除了 \(p\) 别的列高度为 \((\Delta,h_p]\) 这部分（下文称之为染色地方）的染色，分类讨论：

• 如果存在 \(h_p[i]=h_p[i+1](\Delta<i<i+1\leq h_p)\)，\(p\) 的钦定方案数为 \(2^{h_p-\Delta}-2\)，\(h_{p\pm 1}[i],h_{p\pm 1}[i+1]\) 颜色固定，推下去要染色的地方都被确定了，且相邻两位顶的颜色相异（\(h_x[h_p]\neq h_{x+1}[h_p]\)），设 \(g(l,r,\Delta)\) 表示 \([l,r]\) \(\Delta\) 以上的部分在钦定了 \(h_i[\Delta+1]\) 的颜色且保证钦定方式为相邻两列的钦定不同的情况下的方案数，还要乘子问题 \(g(l,p-1,h_p)\) 和 \(g(p+1,r,h_p)\)。

• 如果不存在 \(h_p[i]=h_p[i+1](\Delta<i<i+1\leq h_p)\)，\(p\) 的钦定方案数为 \(2\)，此时可以随便钦定 \(h_x[h_p]\)，剩下的部分推下去可以被确定，发现是子问题 \(f(l,p-1,h_p-1)\) 和 \(f(p+1,r,h_p-1)\)。

现在问题只剩 \(g(l,r,\Delta)\) 怎么求了，设 \(p\) 是 \([l,r]\) 中 \(h\) 最小的，满足 \(h_p>\Delta\) 不然递归到满足，任意钦定 \((\Delta,h_p]\) 的颜色别的可以推出，得到子问题 \(g(l,p-1,h_p)\) 和 \(g(p+1,r,h_p)\)。哦 \(f\) 和 \(g\) 的边界是 \(f(l,r,)=1,g(l,r,)=1(l>r)\)。

---

CF1641D

这不是直接二分双指针然后容斥就做完了吗？有人被卡常了嘻嘻。但是不难发现可以去掉二分，然后就能通过了，顺便吐槽一下基数 233 的哈希无法通过。

我们先把这 \(n\) 个序列按照 \(w\uparrow\) 排序，按顺序分别考虑 \(w_i\leq w_1,\dots,w_n\) 时 \(w_j\leq w_{pos}\) 的 \(\min\{pos\}\) 然后让合法的 \(w_i+w_{pos}\) 贡献。我们对 \(1,\dots,i\) 和 \(1,\dots,pos\) 分别开桶，容斥计算合法对数然后双指针即可。

---

CF1365G

按位分讨考虑什么的因为位数太多感觉不太可以，那在 lsy 意义下只能考虑构造询问集合 \(Q_0,\dots,Q_{12}\) 使得所有 \(x\) 可以用 \(Q\) 并出去掉 \(x\) 的部分。

这个有一个非常显然的做法，考虑第 \(i\) 个二进制位为 \(0/1\) 的数的集合或和为 \(Q_{i}(0/1)\)，那么一个 \(p_i=\text{or}\{Q_j(i 的第 j 位\oplus 1)\}\)，正确性显然。但是在这样子要 20 次，瓶颈在于每一位做了 \(2\) 次，但是这个题目显然不支持我们每一位做 \(2\) 次，我们先考虑一下每一位做 \(1\) 次为什么不行，我们只做 \(Q_j(1)\) 的话，如果出现 \(i\) 是 \(i'\) 的子集，那就会寄掉一个。

现在问题变成了构造值域不超过 \(13\) 位的序列 \(id_1,\dots,id_n\) 使得 \(id\) 互不为子集，如果我们构造 \(id[x]=0\) 那就完蛋了，构造 \(id[x]=1/2/4/8\) 这种 \(bitcount=1\) 的就浪费一个二进制位，构造 \(id[x]=3\) 差不多就是浪费 \(\frac{1}{4}\) 的编号......构造 \(bitcound\) 不同的 \(id\) 感觉麻烦且难优，不妨考虑构造 \(bitcount\) 相等的 \(id\)，那么显然 \(\binom{13}{6}\) 和 \(\binom{13}{7}\) 是最棒的啦，而这个正好够 \(n\) 使用了，然后就做完了。

---

P8512

不会在线，在 lsy 意义下只能离线，现在要考虑加入右端点 \(i\) 和查询 \([l,i]\)。

首先类似 ODT 那样维护段，一个区间操作最多切割多 \(2\) 段，加入 \(1\) 段，暴力做总段数级别在 \(O(n)\)，那就暴力做，暴力加暴力删，用树状数组维护时间的答案即可。

---

P2801

分块，块中有部分修改就重新排序，整体修改打 lazytag，查询在整块里面二分，非整块暴力。

---

P5857

\(x/y\) 各自的方案数是好算的，所以比较想做成 \(x 的方案数\times y 的方案数\) 这种形式的东西，我们考虑什么情况下有 \(x\neq x',y\neq y'\) 但是 \(mat(x,y)=mat(x',y')\) 的，这要求不存在 \(x_i\oplus y_j\neq x_i'\oplus y_j'\)，也就是只能全部取反了捏。所以我们拿全局方案数减掉这部分即可，都是很好算的。

---

AT_arc114_e

这种过程难以描述贡献比较直白的题目考虑映射成别的游戏，过程的约束用贡献的约束取而代之。我们考虑如下游戏：随便选一条线，如果这条线会导致矩形分割那么贡献 \(+1\)。

对于一条线，有 \(s\) 条边可以在这条边之前选，总共有 \(tot=n+m-2\) 条边，枚举当前时间 \(i\)，那么这条边的期望 \(E(edge)=\frac{1}{tot}\sum_{i=0}^{\infty}(\frac{s}{tot})^i\)，改写成分数形式加起来就可以了，最终的答案加上死的那一下。

---

AT_abc221_h

如果没有 \(m\) 的限制，我们可以考虑 dp，设 \(f[i][j]\) 表示长度为 \(i\) 和为 \(j\) 的方案数，特别的可以有 \(0\) 单调性保持，\(f[i][j]=f[i][j-i]+f[i-1][j]\)，表示整体 \(+1\) 或者加一个 \(0\)。

现在加上 \(m\) 的限制，设 \(g[i][j]\) 表示 \(f[i][j]\) 中没有 \(0\) 的部分其实也就是 \(f[i][j-i]\)，转移可以写 \(f[i][j]=\sum_{t=1}^m g[i-t][j]+f[i][j-i]\)，前缀和优化可以做到 \(O(n^2)\)。

---

CF1239F

感觉这个题目多少有点那啥......？不断找特殊情况分类讨论讨论完就做完了。

设 \(col[x]=in[x]\mod 3\)，我们先处理处所有点的颜色。

• 如果存在 \(col[x]=0\)，如果 \(n=1\) 一定无解，否则只保留 \(x\) 一定是合法的。

• 如果存在颜色全为 \(2\) 的环，那么构造保留一个环，首先如果只有一个颜色全都是 \(2\) 的简单环是无解的，否则考虑在一个环上的点 \((x,y)\)（可以通过 dfs 树求出任意一组），然后找 \(x\to y\) 不经过 \((x,y)\) 的最短路跟这条边组成环。需要最短路是因为对于原图中的一个环我们希望不要有非环上边，最短路刚好满足这个。

如果只存在颜色为 \(2\) 的点但是形成森林一定无解，排除了上面情况现在一定存在且仅存在 \(col\) 为 \(1/2\) 的点，且只看 \(2\) 的子图一定是森林，我们继续分讨：

• 如果存在一个连通块里面有 \(x\neq y\) 使得 \(col[x]=2,col[y]=2\)，保留这两点间的最短路即可。特别的，如果出现形如 \(1-2-\dots-2-1\) 这样的图无解。

• 否则一个连通块中只有 \(1\) 个颜色为 \(1\) 的点 \(rt\)，我们考虑找两个只有 \(rt\) 一个交点的环形成一个 8 字形。注意到，假设一个 \(n\) 个点颜色全都为 \(2\) 连通块（一定是树）连了 \(lnk\) 条边到 \(rt\)，一定满足 \(2\times (n-1)+lnk\equiv 2n\pmod 3\)，也就是 \(lnk\equiv 2\pmod 3\)，换言之，\(rt\) 连接至少两个连通块。为了方便直接随便找两个连通块在里面分别找可以跟 \(rt\) 成环的路径。除非原图就是 8 字形不然一定有解，找的时候要尽量避免选到极大的环，随便选一个 \(rt\) 的连接的 \(x\)，考虑 \(rt\to x\) 不经过 \((x,rt)\) 的最短路即可。

---

AT_agc006_c

朴素 dp 化简之后是 \(f_i'=f_{i-1}+f_{i+1}-f_i\)，有 \(f_i'-f_{i-1}=f_{i+1}-f_i,f_{i+1}-f_i'=f_i-f_{i-1}\)，这个实质是交换差分。一轮等价于把差分的顺序从 \(1,\dots,n\) 变成了 \(p_1,\dots,p_n\)，轮数倍增和增加都是好做的，我们不断让轮数 \(\times 2\) 或者 \(+1\) 得到 \(k\) 最后还原 \(f\) 即可。

---

AT_agc035_e

如果删除一个数 \(x\)，连边 \(x\to x-2,x\to x+k\)，不难发现一种删除方式合法等价于图上无环，有环的一定不合法，没有环的按照 topu 序删就可以了。这个 \(x-2\) 启迪我们按照 \(k\) 的奇偶性分类 dp，我们分别做一下就行了。

对于 \(k\) 是偶数，奇/偶数位不可能互相影响成环，剖成两部分方案数乘起来即可。此时要求不连续选超过 \(\frac{k}{2}\) 个，设 \(f[i][j]\) 表示前 \(i\) 个最后连续选了 \(j\) 个的方案数，有 \(f[i][j]=f[i-1][j-1]\)，特别的 \(f[i][0]=\sum_{t=0}^{\frac{k}{2}}f[i-1][t]\)，最后 \(Ans=(\sum_{i=0}^k f[\lfloor\frac{n}{2}\rfloor][i])\times (\sum_{i=0}^k f[\lfloor\frac{n+1}{2}\rfloor][i])\)。

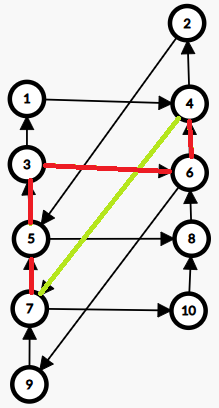
\(k\) 是奇数的稍微难一点，我们考虑按照上图方案按行 dp，\(L=2t-k/0\) 和 \(R=2t/0\) 一行，总共有 \(\lfloor\frac{n+k}{2}\rfloor\) 行。我们发现上图中不存在环的要求其实就是从 \(L\) 往上的最长的一条路径（形如上面的红线）长度 \(\leq k+1\)，所以考虑 \(f[t][i]\) 表示到第 \(t\) 层红色路径最长为 \(i\) 的方案数，但是这样还不够，如果左边被断开了我们需要知道右边连续选了多少个才能更新 \(i\)，所以设计状态 \(f[t][i][j]\) 新加入的一维是右边连续选了多少个。转移考虑 \(f[t-1][i][j]\) 通过 \(t\) 行的 \(L,R\) 能转移到哪里：

• 不删除 \(L,R\)，\(f[t-1][i][j]\to f[t][0][0]\)。

• 删除 \(L\) 不删除 \(R\)，如果 \(i>0\)，\(f[t-1][i][j]\to f[t][i+1][0]\)，否则 \(i=0\)，\(f[t-1][i][j]\to f[t][0][0]\)。

• 删除 \(R\) 不删除 \(L\)，\(f[t-1][i][j]\to f[t][i][j+1]\)。

• 删除 \(L,R\)，如果 \(i>0\)，\(f[t-1][i][j]\to f[t][\max(i+1,j+2)][j+1]\)，否则 \(j=0\)，\(f[t-1][i][j]\to f[t][j+2][j+1]\)。

最后显然是 \(Ans=\sum_{i=0}^{k+1}\sum_{j=0}^n f[\lfloor\frac{n+k}{2}\rfloor][i][j]\)。

---

P7914

首先普通的 dp 设计 \(f[i][(l,r)][k]\) 表示前 \(i\) 个左右括号数量状态为 \((l,r)\) 最后有连续 \(k\) 个，这样不能处理 (*A*) 的情况，如果非要处理要加入 \(2^n\) 这种不能接受的状压。

我们考虑区间 dp，设计 \(f[l][r][0/1/2/3]\) 表示区间 \([l,r]\) 序列形态为 */(...)/*(...)/(...)* 的方案数，dp 是平凡的，但是对于 ()()()/()()*() 这些形态的东西会算重，为了避免算重我们应该钦定序列的产生方式是从极小的地方划开（就是要求左边的 (...) 不能继续划分成 (...)...(...)，右边没有约束），这个不能划分相当于其最左最右的括号匹配。

我们重新设计状态 \(f[l][r][0/1/2/3/4]\) 表示区间 \([l,r]\) 序列形态为 */(...)/(...)/*(...)/(...)* 的方案数，\(opt=1\) 的左右括号匹配，\(opt=2\) 的左右括号不匹配，我们考虑转移：

• \(f[l][r][0]\)，直接暴力判断 \([l,r]\) 可不可以成为 \(长度\leq k\) 的全 * 区间。

• \(f[l][r][1]\)，剖去匹配括号就是子问题了，从 \(f[l+1][r-1][0/1/2/3/4]\) 转移，要求 \(str_l,str_r\) 可以组成 ()。

• \(f[l][r][2]\)，钦定了 1+else(1/2/3) 的转移方式，具体而言枚举分割点 \(i\in [l,r-1]\)，从 \(f[l][i][1]\times f[i+1][r][1/2/3]\) 转移。

• \(f[l][r][3]\)，钦定左边的 * 然后去拼，具体而言枚举分割点 \(i\in [l,r-1]\) 从 \(f[l][i][0]\times f[i+1][r][1/2]\) 转移。

• \(f[l][r][4]\)，与 3 类似，不多赘述。

最后答案就是 \(f[1][n][1]+f[1][n][2]\)。

---

P7916

\(k=2\) 可以类比最小割转对偶图最短路，具体做法不多赘述。然后我们考虑拓展到 \(k\) 更大的情况，首先黑点和白点之间的部分需要有出路径，我们把这部分涂成块，初始我们考虑相邻的块之间有路径，这样不仅不能求而且不能最优，更优秀的情况是这样的路径之间有交，合成大黑块。先预处理出块间最短路（注意这 traffic5.in 部分 dij 本地 3s 但是 spfa 有 40s /fn），然后考虑怎么合成大黑块，发现是环状的 \(s/t\) 匹配路径不交（假设不交的相邻匹配 \((s_1,t_1),(s_2,t_2),(s_3,t_3)\) 可以合成 \((s_1,t_2),(s_2,t_3),(s_3,t_1)\) 这样），dp 即可。

---

ARC083F

我们应该先思考怎样行动是合法的，对于每一个点 \((x,y)\) 连接 \((x,y+n)\)，这样子会形成一个基环树森林（否则存在点度数为 \(0\) 导致无解），我们把每一棵基环树抠出来分别处理，答案是各自的方案数相乘再乘上组合数的贡献，比如说到现在已经处理了 \(sum\) 个点，现在这个连通块有 \(x\) 个点方案数是 \(Ans\)，那么总的答案乘上 \(\binom{sum}{x}\times Ans\)。

对于一棵基环树，现在我们要给每一个点分配一条边，非环上点分配到的边是固定的，环上点可以顺时针/逆时针分配边，我们钦定顺/逆时针，每个点被哪条线（机器人）抓走就确定了。回到原问题，现在仅仅有一些某个机器人必须必某些机器人后行动的约束，不难发现约束形态容易写成森林（只需要钦定 \(0/1\) 个父亲），那么直接计算森林 topu 序数即可，这个是 \(\frac{n!}{\prod siz_x}\)。

---

ARC104F

简单题哈，首先这个东西是一个类似笛卡尔树数量的东西，所以我们考虑区间 dp，设 \(f[l][r][x]\) 表示区间 \([l,r]\) 全都不大于 \(h_x\) 的 \(P\) 的种类数，发现钦定根 \(p\) 必须是最大的下标最右的那个，意思是 \([p+1,r]\) 的子问题要不大于 \(h_x-1\) 这样子，我们考虑状态 \(f[l][r][x][d]\) 表示全都不大于 \(h_x-p\) 的方案数，然后发现因为 \(n\) 很小的话 \((x,d)\) 可以直接缩成 \(v\) 表示不大于某个值，换句话说最开始反正都可以 \(h_x\) 和 \(n\) 取 min 了那直接摊上去真实值呗。

---

AT_arc112_e

首先每个数只有最后一次操作是影响序列长相的，且假设一个前缀 \([1,x]\) 都是左移出的那么它们最后一次操作的顺序已经固定了，后缀同理。我们考虑钦定 \([1,i]\) 是左移出的，\([i+1,j-1]\) 是没有操作的，\([j,n]\) 是右移出的，中间段只要判断单调上升就行了，而两边要考虑的可就多了，我们需要知道 \(f[m][l][r]\) 表示做了 \(m\) 次操作有 \(l\) 个最后一次操作是左移有 \(r\) 个最后一次操作是右移的方案数，这个是 \(g[m][l+r]\times \binom{l+r}{l} \times 2^{m-l-r}\)，其中 \(g[i][j]\) 表示把 \(1,\dots,i\) 涂成恰好 \(k\) 种颜色的方案数。

---

AT_arc121_f

首先有一个很显然的贪心，先做 and 再做 or，所以其实结果能为 \(1\) 相当于存在一个全为 \(1\) 的 and 连通块。已经可以 dp 但是超级麻烦，我们考虑正烦则反，求出 and 连通块结果全为 \(0\) 的方案数，设 \(f[x][0/1]\) 表示子树 \(x\) 目前根所在连通块是不是全 \(1\) 的方案数，转移是好写的。

---

ARC070E

考虑 \(f[i][j]\) 表示第 \(i\) 条线段左端点在 \(j\) 的最优答案，那么 \(f[i][j]=\min_{k\in[j-(r_{i-1}-l_{i-1}),j+(r_i-l_i]}\{f[i-1][k]\}+|j-l_i|\)，是一个模板 slope trick，对顶堆维护即可。

---

P8820

对于 \(k=1\)，求的是路径权值和，求解 lca 之后差分一下就行了。

对于 \(k=2\)，设 \(f[i][0/1]\) 表示点 \(i\) 选/不选的最优价值，\(j\) 是 \(i\) 的前继节点，转移有 \(f[i][0]=\min\{f[j][0],f[j][1]\}+v_i\)，\(f[i][1]=f[j][0]\)，倍增+矩阵乘法优化即可，矩阵乘法这里定义为和的最小值（类似邻接矩阵快速幂那种乘法）。

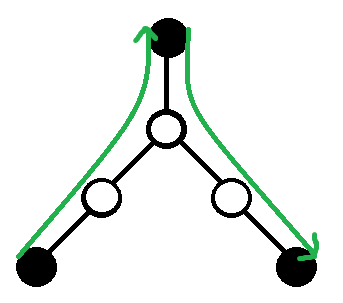
对于 \(k=3\)，首先发现点不一定在 \(s\to t\) 路径上，但是还好贡献方式非常的单一，只有上图一种，那我们可以沿用类似 \(k=2\) 的做法就行了，设 \(f[i][0/1/2]\) 表示还能填 \(0/1/2\) 个白的最优价值，转移有 \(f[i][0]=f[j][1]\)，\(f[i][1]=\min\{f[j][2],v'[i]+f[j][1]\}\)，\(f[i][2]=v_i+\min\{f[j][0],f[j][1],f[j][2]\}\)，其中 \(v'[i]\) 表示 \(i\) 围着的一圈的 \(v\) 的最小值。

---

P7078

整个过程如果不能终止的话就是 \(n-1\) 个二元组 \((x,y)\) 表示 \(x\) 吃掉 \(y\)，注意到有 \(n-1\) 个点被吃掉且一定联通，所以这是一棵外向树，且 \(x\to fa_x\) 一定比 \(fa_x\to fa_{fa_x}\) 早出现。

对于一个点 \(x\)，感觉影响比较大的只有 \(x\to fa_x\) 和最后出现的一条 \(y\to (fa_y=x)\)，后者留着一定能保证 \(x\) 不死，前者决定了 \(x\) 能不能贪刀（有时候 \(x\) 的父亲需要保留这条边来保证自己不死，此时 \(x\) 不需要留边保平）。我们称上述的第二类边为重(zhong)边，发现如果轮到了重边 \((x,y)\)，因为 \(fa_x\) 不可能最终吃掉 \(x\) 所以要么 \((x,y)\) 结束，要不然 \((fa_x,x)\) 结束，问题变成了 \(x\) 能不能贪刀。

首先只有这两条边出现时间之间出现的边才有用了，别的都被厌弃了，所以这个是子问题。首先如果这中间还有形如上面的边对（重边上面有边），那一定贪刀，然后递归子问题；否则中间一定是菊花边是无用的，这种情况相当于 \((x,fa_x)\) 之后直接轮到 \((fa_x,fa_{fa_x})\)，我们称一个需要重边保护的点是弱点，不需要重边保护的点是强点，如果重边上面是非重边那这一定是弱点，然后只需要考虑一条重链的情况，不难发现强点后面一定是弱点，弱点后面一定是强点，特别的，根是强点，于是就可以求出游戏进行到什么时候了。

还有一个预处理的问题，暴利是 set/大根堆之类的，但是怎么在低于 \(O(n\log n)\) 的时间求出抓人序列，首先猜测观察打表什么的应该可以发现 \(A_{\max}-A_{\min}\) 单调不升，所以我们维护两个单调的序列 \(p,q\)，分别表示原蛇（绝对没有谐音 Genshin）和新蛇，我们证明一下，首先 \(A_{\max}\) 单调性符合，\(A_{\min}\) 如果是原神的话单调性肯定也符合，如果是新蛇的话我们分析一下，假设 \(q2\) 是 \(x,\dots,x+\Delta\)，如果 \(\Delta>x\) 肯定不影响单调性，否则操作后变成 \(\Delta,\dots\)，其中 \(\dots\in[x,x+\Delta]\)，同时 \(q1\) 中的最大也满足 \(A_{top of q1}\leq x+\Delta\)，于是新的 \(A_{\max}-A_{\min}\leq \Delta\)，证毕。但是写完你会发现编号不一定有单调性，再手调一下就好了，复杂度好像不太被保证，但我真的懒了。

---

P5684

计算中间数的贡献后插入数字即可。

---

P5682

猜测有用的不多那塞点相邻不多位的结果取 max 就过了。

---

P9754

按照题意模拟即可。

---

P7075

按照题意预处理出一些年份 \(1.1\) 的儒略日，可以以 2000 年为上界方便后面计算闰日数，二分出年份，暴力一点计算出日期。

---

P8868

区间困难问题考虑扫描线，离线固定 \(r\) 来简化问题，这样子对于每个左端点 \(l\) 其 \(\max_{i\in[l,r]} x/y_i\) 容易用单调栈简单维护，在这之后我们还需要维护如下操作：

• \(i\in[l,r]，x/y_i\gets v\)

• \(ans_i\gets ans_i+x_i\times y_i\)

• 查询 \(\sum_{i\in[l,r]} ans_i\)

考虑使用线段树，容易发现困难点在于你至少有 \(tag_x,tag_y,c\) 三种 lazy_tag 分别是 \(x/y\) 的区间覆盖和 \(c\) 次版本和，为了复杂度不能下传标记而这三个又不能简单合并。我们不妨先考虑一下在当前节点，怎么将一串（线性长） lazy_tag 转化成一坨（常数长），然后再考虑对子孙的影响。

• \(ans_i\gets ans_i+x_i\times y_i\)

1. 有 \(tag_x,tag_y\)：

对于当前点，直接做 \(ans\gets ans+tag_x\times tag_y\times len\) 即可。

对于子孙来，影响关心的 \(len\) 不知道但可以提出来，所以应该下传 \(\sum tag_x\times tag_y\)，这个到后面累加进同类 lazy_tag 里面 & 乘上 \(len\) 加到 \(ans\) 里面就行了。

2. 只有 \(tag_x\) 没有 \(tag_y\)：

对于当前点，直接做 \(ans\gets ans+tag_x\times \sum y\) 即可，容易额外维护 \(\sum y\)。

对于子孙，影响关心的 \(\sum y\) 不知道但可以提出来，所以应该下传 \(\sum tag_x\)，这个到后面累加进同类 lazy_tag 里面 & 乘上 \(\sum y\) 加到 \(ans\) 里面就行了。

3. 只有 \(tag_y\) 没有 \(tag_x\) ：

显然相当于 2，需要额外维护 \(\sum x,\sum c\times tag_y\)。

4. 没有 \(tag_x,tag_y\)：

对于当前点，直接做 \(ans\gets ans+\sum x\times y\) 即可。

对于子孙，影响关系的 \(\sum xy\) 不知道但可以提出来，所以应该下传 \(\sum 1\)，这个到后面累加进同类 lazy_tag 里面 & 乘上 \(\sum xy\) 加到 \(ans\) 里面就行了。

• \(i\in[l,r]，x/y_i\gets v\)

发现是非常普的区间覆盖，暂时对别 \(ans\) 直接相关的标记没有影响。

对于当前点做 \(x\gets v,y\gets v\) 顺便修改 \(\sum x,\sum y,\sum xy\) 即可。

综上我们应该至少维护 \((tag_x,tag_y,uxy=\sum tag_x\times tag_y,ux=\sum tag_x,uy=\sum tag_y,u=\sum 1,\sum x,\sum y,\sum xy,ans)\) 这么多的信息，非常的恶心。

然后这么多标记信息还是不能太敷衍顺序的，依赖子树历史信息的就只有 \(u(x)(y)\)，先下传这些就行了。

---

P7962

首先对于巨大柿子进行化简，得到答案为 \(n\times \sum a_i^2-(\sum a_i)^2\)。

这个 \(a_i\gets a_{i-1}+a_{i+1}-a_i\) 不是很好搞，考虑转化一下操作，是一个很典典典的差分交换，特别的 \(d_1\) 是固定的（不难发现这个其实连贡献都没有 w）。

然后应该是要 dp 了，比较基础的想法是把 \(\sum a_i\) 当成一维状态不断往后填，但这样完全没办法确定用于转移的 \(\Delta\)，如果按照 \(\Delta\) 去枚举又完全没有办法确定位置。注意到这俩不太像可以优化的东西，只能猜测差分序列的排列方式有明显规律。

首先肯定是猜测单调上升/下降什么的，但是 simple 就是一个 hack 了，所以启动 打表 大法，然后发现 \(d\) 是单谷的 qwq

那我们按照 \(\Delta(d)\uparrow\) 的顺序填表，那有填在前面/后面两种方法，发现贡献需要知道一个 \(\sum a_i\)，于是设计状态 \(f[i][j]\) 表示填了前 \(i\) 个差分序列和是 \(j\) 的最大 \(\sum a_i^2\)，记 \(pre_i=\sum_{j=1}^i d_j\)，有以下转移：

• 放在左边，\(f[i][j]\to f[i+1][j+(i+1)\times \Delta]\)，变化 \(a_i^2\to (a_i+\Delta)^2\) 以及左边多出一个 \(a=\Delta\)，额外代价 \((i+1)\times \Delta^2+2\Delta j\)

• 放在右边，\(f[i][j]\to f[i+1][j+pre_{j+1}]\)，变化右边多出来一个 \(pre_{j+1}^2\)，额外代价就是这个

这样子 dp 复杂度是 \(O(n^2\times a)\) 的，无法通过，你盯着数据范围沉思半天你发现跑步过去的点有好多洛零，而这种转移没有贡献，于是复杂度剪一下就是 \(O(\min(n,a)\times an)\) 了。

---

P9118

设 \(f(i)/g(i)\) 表示 \(x=a^i(x\leq n)\) 要求/不要求最大化 \(i\) 的 \(x\) 的个数，显然 \(g(i)=\lfloor n^{\frac{1}{i}}\rfloor\)，\(g(i)=\sum f(ki)\)，于是倒序容斥即可，需要特殊处理 \(1\)。

---

P9119

发现相交只会劣，于是变成了一个类似交通规划 dp 部分的东西，考虑区间 dp，观察到最后点一定在边缘，设 \(f[l][r][0/1]\) 表示挂完 \(l,\dots,r\) 的情况下结尾在 \(l/r\) 的最优代价，转移和构造方案是简单的。