2024.5 总结2 / 共同看 浮岛尽数下坠 可笑又可悲
感觉五月一个五一假期 + APIO 搞得都没几天能做题了......?
P10102
感觉评绿低了,根本就秒不掉 /fad
随机一个 \(1\times n\) 的矩阵 \(V\),判定 \(D\times A\times B\) 是否等于 \(D\times C\) 即可。
CF1205C
曼哈顿距离为 \(2\) 的询问可以解决黑白之后的问题,再用询问翻一组看看需不需要取反即可,代码没写,因为感觉很 gosh。
CF1580B
很显然要求的等价于,由大小为 \(n\) 的排列构成的深度为 \(m\) 的点恰好有 \(k\) 个的方案数。
很显然可以 dp,这个深度很难剖出来,直接放在状态里面。不妨设 \(f[i][j][k]\) 表示大小为 \(i\) 的子树根的深度为 \(j\) 深度为 \(m\) 的点有 \(k\) 个的方案数,初始化 \(f[0][i][0]=1\),注意空子树的深度应该有假定为 \(n+1\) 的部分,转移也是很显然的嗷!
但是仍然无法通过此题,但是显然可以剪枝,剪剪就过了 qwq
CF1458C
比较容易显得人智力不佳的题目,嘻嘻。只有 UDLR 应该是直接做就行了的,但是 IC。
考虑离散一点的意义:对于 \((i,j,a_{i,j})\) 交换 \((i,a_{i,j})/(j,a_{i,j})\),然后前面那些 shaber 操作直接单点加量然后取模就是了。
所以维护每一个坐标最终位置以及增量就做完了......?
CF1491G
最近手气不佳,全都分类讨论题 /yun
考虑正常的置换环,发现有两个位置是负的,不行,两个环套一起做,行。
随便换一组,拼接环,然后直接做置换,最后换回那一组即可。
但是如果有奇数的剩余环,那就可以用后备隐藏能源,随便接在一个好点上做就行了。
如果是单独一个环,那就先置换一组,然后往里面做置换然后会出现 \((-y,-x)\) 的这种东西而非目标 \((y,x)\),手玩感觉步数不够,我们不妨停在 \((-x,-z,y)\) 这样一组来还原 \((y,z,x)\),步数刚好够。
AT_agc001_f
考虑一个新序列 \(a'\) 满足 \(a'_{a_i}=i\),可以看做值指向位置,现在交换要求是相邻差 \(\geq k\),目标是小的往左指,归并排序即可,需要维护一个后缀 \(\min\)。
CF1608F
怎么有人觉得 *3200 是下位紫 & 简单 dp 呢,点名批评 Lgx_Q。
首先状态设计,\(f[i][j][k]\) 表示考虑了前 \(i\) 个数,此时的 \(\text{mex}\) 为 \(k\),\(>k\) 的数有 \(j\) 种的方案数,核心思想是对于目前不关键的延算贡献,然后考虑 gosh 一样的转移,下面 \(\gets\) 表示加的贡献(
对于 \(\text{mex}\) 不变的:
-
放进已有种类 \(f[i][j][k]\gets f[i-1][j][k]\times (j+k)\)
-
创建一个不影响的种类 \(f[i][j][k]\gets f[i-1][j-1][k]\)
对于 \(\text{mex}\) 变化的:
- \(f[i][j][k]\gets f[i-1][j+k-p-1][p]\times A_{j+k-p-1}^{k-p-1}\)
不妨设 \(m\gets j+k-1\),那么有 \(j!\times f[i][j][k]\gets f[i-1][m-p][p]\times (m-p)!\)
可以使 \(g[i][m][t]\gets\sum_{i=0}^{t}f[i][m-p][p]\times (m-p)!\) 来优化,然后就做完了。
注意亿点点细节,或者贡献可以想办法直接在 \(f\) 里面展开。
CF573E
大暴力可过,乐乐乐乐乐乐乐乐乐。
ARC061F
简单题。
考虑构造双射这类东西,发现操作序列就够了,对操作序列的要求如下:结尾为 \(1\),\(1\) 有 \(n\) 个,\(2/3\) 分别不超过 \(m/k\) 个,其对应在原题目的方案数为 \(3^{n+m+k-序列长度}\),现在考虑怎么求一个长度为 \(n+d\) 的序列的方案数,不妨设其为 \(s(d)\),那么 \(Ans\gets \sum_{i=0}^{m+k}3^{m+k-i}s(i)\)。
首先抽出 \(1\),显然有 \(s(d)=\binom{n+d-1}{k}\sum_{j=0}^d [j\leq m][d-j\leq k]\binom{d}{j}\),前面那么没什么问题,后面那个可以线性递推,初二的时候 lby 给过一个差不多的,当时现场会了嘻嘻,然后就做完了。
AGC032E
随便猜猜就过了,详细证明没想,主要写思路。
首先不难发现题目等价于做 \(0\text{~}n\) 次单点 \(-M\) 之后两两匹配的最大值最小是多少,但是多了一个额外的要求最小匹配的权 \(\geq 0\)。
不考虑这个唐诗的条件,显然直接使得 \(a\uparrow\) 然后在一个后缀上面 \(-M\),这串后缀按照新的大小应该移到开头,然后最大最小匹配就行了。在下面的给最大的不劣性可以交换试试.....?
有时候这个最大最小直接匹配可能会有 \(<0\) 的喵那怎么办呢,如果最大匹配最小不行的话,别的就更不行了,交换也不优(假设 \(a'\leq a\leq 0\leq b\leq b'\) 有 \(a+b\geq 0,a'+b'<0\),此时 \(a'+b\) 还是会 \(<0\),不会让可行性更好,更不会让答案更好),所以肯定有次数直接匹配能取到全局最优解。
这样子还是平方的,考虑操作次数越来越多的话,不考虑限制的话,答案会越来越好的,那么考虑操作 \(n,\dots,0\) 次,对应的情况应该是先不可行,然后答案越来越差,所以二分出第一个可行的位置就是最优秀的了捏 qwq
AGC010E
显得我唐诗题,首先对于一组不互质的数,其相对顺序应该在先手序列里面直接被给出,否则随意。
考虑对不互质的数连边,问题变成了钦定一个 DAG 使得最大字典序最小,后手的操作就直接求出最大字典序的拓扑序,考虑先手怎么做,首先连通块互不影响,考虑一个连通块怎么做。
肯定钦定最小的为没有入度的点,然后发现割开了若干无所谓的连通块,分别求解,一个子连通块也是直接钦定能选的最小就行了,然后这个能选的最小一定跟父亲有边,所以钦定的部分写一个 dfs 即可。
P4066
费用流做法是唐诗,然后 \(O(n^3)/O(n^2\log n)\) 的 dp 也很显然,感觉 dp 优化之后跟贪心等价,但是我基本功不够好。
贪心证明,膜拜 lyl,但是不明白为什么讨论区有人觉得降黄降绿,我觉得很困难且不显然啊!
比如序列 1,6,14,2,11,7,3,15,8,4,9,10,5,我们画出贪心的图。
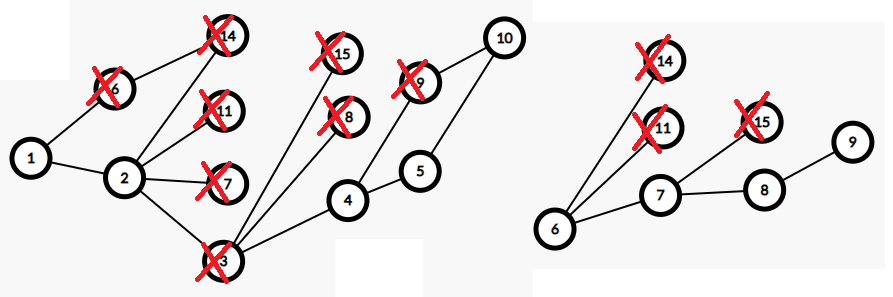
首先对于每一个时刻都有竖着每一个位置的单调递减,横着每一个位置单调不降,这保证了进入第二个辅助数组的顺序正确并且大小关系一定!换句话说,其实第二个数组的结构是第一个数组去掉 顶/底,为什么呢?一个杀掉一个组成双射的话,这两个是等价的。
拓展的说,这个类似双射也就是 lyl 说的 “替换” 关系其实是很强的很普遍的!然后要求最优的两个嘛,你会发现扣掉一条不劣是吧,剩下的部分就是在辅助数组里面再求一次,辅助数组就是扣掉之后的结构(
启发大概是要学会画画 & 对于一些很强的性质要想的大胆一点。
膜拜 zxy,现在我也觉得这玩意显然了。
CF896C
随机数据暴力能过(狗头。推平之后相等区间实际长度不多,期望只有 \(\log\),可以用一个 set 维护,注意 split 先右再左。
AT_joi2013ho5
离散化之后就是 loj 花火,注意贡献和条件有一点点不一样。
CF1733E
首先合并是假的,曼哈顿距离是定的,一个时刻某一个点有没有不好求,但是直到某一个时刻到过某一个点的是好求的,递推求出然后差分即可。
具体而言,考虑一个点 \(d(x,y)\) 往旁边的贡献,显然是向右 \(\lceil\frac{d(x,y)}{2}\rceil\to d(x+1,y)\),\(\lfloor\frac{d(x,y)}{2}\rfloor\to d(x,y+1)\)。
P6860
考虑怎么求解 \(p(a,b)\),充分必要条件是可以走到 \((1,0)\),本质不同的行走方式只有 \((a,b),(b,a),(-a,b),(-b,a)\),不妨设分别用了 \(x_1/x_2/x_3/x_4\) 次,不难化简到 \((a-b)X+(a+b)Y=1\),比起普通的裴蜀定理只是多了一个系数奇偶性相同,分讨一下不难得到多出来的是一个奇偶性不同的约束,所以 \(p(a,b)=[a\bot b][a,b异奇偶]\)。
我们考虑 \(w(x)\) 表示 \(1,\dots,x\) 中跟 \(x\) 互质的奇数,礼貌特判掉 \(1\),首先对于偶数,\(w(x)=\phi(x)\),然后对于奇数,\(\gcd(x,k)=1\Leftrightarrow \gcd(x,x-k)=1\),所以其实是一一对应的,所以 \(w(x)=\frac{\phi(x)}{2}\)。
不妨考虑奇数/偶数的前缀和分别为 \(Ans_1/Ans_2\),不妨对每个数 \(/2\) 来递推 \(Ans_2\),考虑欧拉函数的变化,不难发现 \(Ans_2=2Ans_2(\lfloor\frac{n}{2}\rfloor)+Ans_1(\lfloor\frac{n}{2}\rfloor)\),容斥之后可以得到 \(Ans_1(n)=\sum_{i=1}^{n}\phi(i)-Ans_2(n)\),已经可以做了,但是显然 \(Ans_1(n)+Ans_2(n)\) 这个东西的递推式很美观,就直接 \(Ans(n)=Ans(\lfloor\frac{n}{2}\rfloor)+\sum_{i=1}^{n}\phi(i)\),实现的时候需杜教筛预处理需要多给一点。
AGC027F
考虑枚举第一个操作修改父亲的点为 \(i:(x\to y)\),这样子之后 \(i\) 就不能动了,可以钦定为根。
然后考虑怎么求出答案?首先求出每个点 \(i\) 在 \(A/B\) 中的父亲为 \(L[i]/R[i]\),父亲一样的点不需要操作,因为操作了就操作不回来了,这样的话,有一个条件就是父子关系,父亲操作孩子必然需要被操作,不然无法成功操作。那么操作的点集很好钦定,我们再考虑操作点的顺序,在 \(A\) 中,先操作孩子再操作父亲,在 \(B\) 中,先操作父亲再操作儿子,这要求关系必须是拓扑图,判定一下就行了。
P10454
绿题,考虑移动空格对拍下来的序列的逆序对的影响,发现不影响其奇偶性,于是判定两个状态奇偶性是否相同即可。
必要性显然,充分性大概可以考虑一圈一圈围起来,大小为 \(3\) 之后考虑爆搜数字华容道还原发现只有本质不同的两组。
CF1699E
数据范围给了 \(\sum m\) 的约束,不妨考虑枚举只使用 \(\geq d\) 的情况(相当于左端点),然后考虑最小的右端点,不妨设 \(f[i]\) 表示当前值为 \(i\) 的数在只用超过 \(\geq d\) 的分解的情况下的最小右端点,特别的,无解的令 \(f[i]\gets \infty\),\(d\) 的答案就是 \(\max_{i\in a}\{f_i\}-d\),这个东西的最小值就是答案。
从 \(d+1\) 递推到 \(d\),显然只有 \(f[i](d|i)\gets f[\frac{i}{d}]\) 这样的更新,哦还有 \(f[d]\gets d\),箭头表示取 \(\min\) 的贡献,诶那这个暴力更新复杂度就只有 \(O(m\log m)\) 了,那个动态最大值可以用优先队列维护,然后做完了。
P4363
考虑对轮廓线进行 dp,首先有效状态只有 \(\binom{n+m}{n}\) 这么多,哦这不是很多,不妨用 \(0/1\) 表示向上/向右,一个长度为 \(n+m\) 的 \(n/m\) 个 \(0/1\) 的二进制串就能表示轮廓线。
转移就直接转移就可以了喵,但是注意博弈论的效性这个题目要倒着转移,拓扑关系不明显可以 dfs 来算 /fad
CF1612F
首先不难发现,对于 \(\leq \min(n,m)\) 的部分,可以倍增的这样子取非常的优秀,上界只有 \(2\log \min(n,m)\),然后对于剩下的部分,通过一个的 \(\max\) 一步一步取一定不劣,我们考虑用答案作为轮进行 dp 知道一个达到顶,剩下的部分直接贪心。
不妨钦定 \(n\leq m\) 否则交换,迭一个当前轮数 \(Ans\),考虑 \(f_i\) 表示在 \(L\) 中选到 \(i\) 的情况下在 \(R\) 中最大选到 \(R_{f_i}\),然后这个转移还是比较 navie 的,就比如我们现在要变换状态 \(f\to g\),然后 \(\gets\) 表示一个取 \(\max\) 的贡献,大概是这样一个东西。
打造 \(L\) 中的:\(g_j\gets f_i(i\leq j\leq f_i+i)\),打造 \(R\) 中的:\(g_i\gets f_i+i\)。但是还有一个列表的贡献,不难发现这个 \(+1\) 的贡献比较的滑稽,就是完全无法跨越的,对于一对 \((i,j)\),如果 \(f_i\geq j\),有一个 \(f_{i+j+1}\gets f_i,f_i\gets i+j+1\) 这样的贡献。
这个东西 \(O(n)\) 暴力做直到 \(f[n]\geq n\),这个只有 \(O(\log n)\) 轮,复杂度 \(O(n\log n)\),那个区间 \(\max\) 可以直接塞一个优先队列维护,之后只需要 \(f[n]\) 就不劣了,暴力跳出去就行了喵 qwq
AT_joi2017ho_b
模拟赛题,考场想麻烦了一点时间。
考虑对每一段进行贪心的放,我们先处理出 \(t'\gets t-(s_i-1)\times C\),然后当成普通一段好的,不妨设标号为 \(0,\dots,len\),我们考虑不用额外次数能跳多少,显然是 \(\lfloor\frac{t'}{C}\rfloor\) 对吧,我们再考虑继续放车站,显然是要放在第一个不能跳到的地方(前面的不用放就有贡献了,后面的有一个尽量后的站是不劣的),那么能多放几个站呢?不妨设以前能到的最后一个站是 \(pre\),显然是 \(\lfloor\frac{t'-pre\times C}{A}\rfloor\) 个站点,由于 \(pre\uparrow\),所以 \(new\downarrow\),直接把贡献塞进数组里排序贪心取即可喵。
AT_joi2017ho_c
模拟赛题,考场想麻烦了亿点时间。
肉眼有一个二分,现在考虑极差能不能 \(\leq d\) 啦,然后不难发现省份分界是轮廓线。
不难发现最大最小值(不妨设为 \(L,R\))肯定有贡献,可以的话一定分到不同的省份,并且是该省份的 rmq,所以得到了两个省份的范围分别是 \([L,L+d],[R-d,R]\),我们就能知道每个小格子能不能属于某一个省,然后我们分类讨论之后 dp 求出能不能划分出合法省份即可。
CF1245F
直接数位 dp 即可。
AT_abc138_f
首先 \(y\mod x<x\),所以这里的 \(x\oplus y<x\),所以 \(y<2x\),然后 \(y=x\oplus y\) 的话 \(x=0\) 不合法,所以 \(y-x=x\oplus y\),数位 dp 求出即可。
P5369
考虑一个前缀和 \(\sum_{i=1}^{x}p_i\) 充要的条件:对于前缀 \([y,x](y<x)\) 要有 \(\sum_{i=y}^x p_i<0\),以及对于后缀 \([x,y](x<y)\) 要有 \(\sum_{i=x}^y p_i\geq 0\),对着这个做状压 dp 即可。
CF1320D
不难发现就是可以将 \(0\) 位移 \(2\),但是不能跨越,于是考虑 \(0\) 的奇偶性序列是否一致即可,不妨哈希,需要维护两种,取模卡 \(10^9+7\),\(998244353\) 过了。
AT_arc135_d
转换操作,黑白染色的一种点取反权,然后发现操作 行/列 和不变,考虑行/列和为 \(x/y\),然后不难发现可以取到理论下界 \(\max(\sum|x_i|,\sum|y_i|)\),然后考虑随便构造就行了。
AT_joi2018ho_b
lgj 模拟赛复活一下。
先使 \(a\uparrow\),然后任意区间合法,线段树优化 dp 即可,直接贪心也行的喵。
AT_joi2018ho_c
lgj 模拟赛复活两下。
我们用 \(G\) 代表一个串,不容易但是可以发现对于一个 \(G\) 来说,如果另一个 \(G\) 所代表的串跟其重合,只有可能这个 \(G\) 在其右上角或左下角(对角线上距离为 \(1\))且方向不同,那么不同对角线贡献不影响,于是不妨设 \(f[i][j][0/1/2]\) 表示在 \(i,j\) 所在的对角线上面 dp 到了 \((i,j)\) 且其 取/取横/取竖 的最优答案,直接 dp 即可。
AT_joi2018ho_d
lgj 模拟赛复活三下。
不难发现是要将一条 \(s\to t\) 的最短路置成 \(0\) 之后的 \(u\to v\) 的最短路,不难想到这个置零的最短路在一个 DAG 上面,那么现在要在图上对 \(u\to v\) 做一个置 \(0\) 权都在一条 DAG 路径上的最短路。
这个一条 DAG 路径在最短路意义下面好像不好直接表示,但是其实不难发现最多走一段就不劣了,于是直接分层图最短路就做完了,置 \(0\) 路径按照 DAG 的同方向,走正着一次反着一次就行了。
AGC016E
不妨考虑 \(f[i][j]\) 这种东西表示如果想留下 \(i\) 是否需要炖掉 \(j\),然后发现这个东西应该倒序考虑,考虑一个新的含义:在某一个时刻想要留下 \(i\) 是否需要留下 \(j\),这个直接做就行了(
然后现在是要想办法判定一对 \((i,j)\) 是否可以共存,考虑留下 \(x\) 需要保留的鸡的集合为 \(S_i\),如果有一个 \((i,x)\) 的操作,那么为了保证 \(x\) 不被删除,\(x\) 应该受到与 \(x\) 同等的保护,所以条件是 \(S_i,S_j\) 不能有交。
CF441E
不妨考虑 \(f[i][j]\) 表示操作了 \(i\) 次有 \(j\) 次增加的期望,考虑转移,首先 \(f[i][2j]\gets f[i-1][j]\),还有 \(f[i][j]=\gets [i-1][j+1]\),注意转移的是期望相同的状态。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号