归并排序

归并排序

将两个的有序数列合并成一个有序数列，我们称之为"归并"。
归并排序是使用分而治之策略作为提高排序算法性能的一种方法。

1. 分解 :将当前区间一分为二；
2. 求解: 递归地对两个子区间进行归并排序，递归的终结条件是子区间长度为1。
3. 合并：将已排序的两个子区间归并为一个有序的区间。

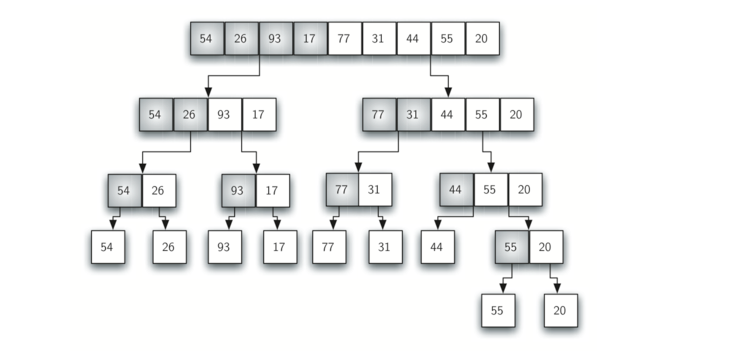
下图展示将列表进行分割的操作过程：

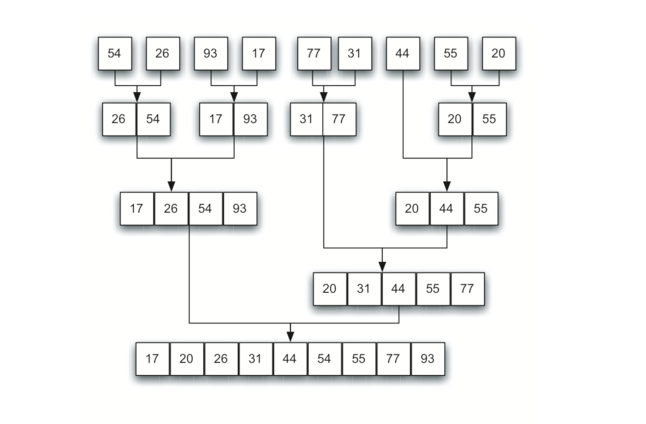
下图展示将排序后的链表进行合并的过程：

归并排序实现

def mergeSort(alist):
    print("Splitting ",alist)
    #列表元素个数小于等于1是基本情况
    if len(alist)>1:
        mid = len(alist) // 2
        lefthalf = alist[:mid]
        righthalf = alist[mid:]

        #递归调用归并排序
        mergeSort(lefthalf)
        mergeSort(righthalf)

        i=0
        j=0
        k=0

        #左右两边比较取小者添加到列表中
        while i < len(lefthalf) and j < len(righthalf):
            if lefthalf[i] < righthalf[j]:
                alist[k]=lefthalf[i]
                i=i+1
            else:
                alist[k]=righthalf[j]
                j=j+1
            k=k+1    

        while i < len(lefthalf):
            alist[k]=lefthalf[i]
            i=i+1
            k=k+1

        while j < len(righthalf):
            alist[k]=righthalf[j]
            j=j+1
            k=k+1
    print("Merging ",alist)

测试：

alist = [54,26,93,17,77,31,44,55,20]
mergeSort(alist)
print(alist)

结果：

Splitting  [54, 26, 93, 17, 77, 31, 44, 55, 20]
Splitting  [54, 26, 93, 17]
Splitting  [54, 26]
Splitting  [54]
Merging  [54]
Splitting  [26]
Merging  [26]
Merging  [26, 54]
Splitting  [93, 17]
Splitting  [93]
Merging  [93]
Splitting  [17]
Merging  [17]
Merging  [17, 93]
Merging  [17, 26, 54, 93]
Splitting  [77, 31, 44, 55, 20]
Splitting  [77, 31]
Splitting  [77]
Merging  [77]
Splitting  [31]
Merging  [31]
Merging  [31, 77]
Splitting  [44, 55, 20]
Splitting  [44]
Merging  [44]
Splitting  [55, 20]
Splitting  [55]
Merging  [55]
Splitting  [20]
Merging  [20]
Merging  [20, 55]
Merging  [20, 44, 55]
Merging  [20, 31, 44, 55, 77]
Merging  [17, 20, 26, 31, 44, 54, 55, 77, 93]
[17, 20, 26, 31, 44, 54, 55, 77, 93]

参考:

1. 演示动画