二分查找

二分查找从中间项开始，而不是按顺序查找列表。 如果该项是我们正在寻找的项，我们就完成了查找。 如果它不是，我们可以使用列表的有序性质来消除剩余项的一半。重复这个过程，直到找到我们的查找项或者确定查找项不存在。
下图展示了该算法如何快速地找到54：

def binarySearch(alist,item):
    first = 0
    last = len(alist) - 1
    found = False

    while first <= last and not found:
        midpoint = (first + last) // 2
        if alist[midpoint] == item:
            found = True
        else:
            if item < alist[midpoint]:
                last = midpoint -1
            else:
                first = midpoint +1

    return found


testlist = [0, 1, 2, 8, 13, 17, 19, 32, 42,]
print(binarySearch(testlist, 3))
print(binarySearch(testlist, 13))

递归实现：

def binarySearchRec(alist,item):
    if len(alist) == 0:
        return  False
    else:
        midpoint = len(alist) // 2
        if alist[midpoint] == item:
            return True
        else:
            if item < alist[midpoint]:
                return binarySearchRec(alist[:midpoint],item)
            else:
                return binarySearchRec(alist[midpoint+1:], item)


testlist = [0, 1, 2, 8, 13, 17, 19, 32, 42,]
print(binarySearchRec(testlist, 3))
print(binarySearchRec(testlist, 13))

查找性能情况：

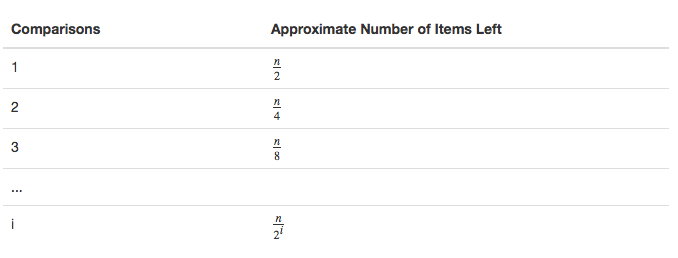
求解 i 得出 i=logn 。 最大比较数相对于列表中的项是对数的。 因此，二分查找是 O(logn)。
Python中的 slice 运算符实际上是 O(k)。这意味着使用 slice 的二分查找将不会在严格的对数时间执行。幸运的是，这可以通过传递列表连同开始和结束索引(第一种实现方式)来纠正。
即使二分查找通常比顺序查找更好，但重要的是要注意，对于小的 n 值，排序的额外成本可能不值得。事实上，我们应该经常考虑采取额外的分类工作是否使搜索获得好处。如果我们可以排序一次，然后查找多次，排序的成本就不那么重要。然而，对于大型列表，一次排序可能是非常昂贵，从一开始就执行顺序查找可能是最好的选择。