使用位运算计算一个二进制数中值为1的个数
使用位运算计算一个二进制数中值为1的个数
二进制
电脑采用二进制的原因其实很简单!
因为二进制的0和1正好对应了计算机中逻辑电路开和关两种状态
所以为了方便表示,就用1代表高电平,0代表低电平
(不止开关,很多元器件的状态大多数也只有两种)
这样更加容易表示,运算规则也比较简单(计算机比较笨!)
传输数据是也可以只用电压高低就能表示数据
(网线就是八根铜丝儿电压高高低低的传输数据)
十六进制
十六进制的存在更多是为了服务二进制
毕竟一个正常的二进制数都老长老长了
(一个字节有8位二进制数,但是转化成十六进制就只有2位)
(0xFF和0B11111111的差别)
为了方便运算,而且不让程序员看0和1看的头晕眼花,所以有了十六进制
与十进制不同的是,十六进制由于基数(就是逢多少进一)的问题
所以每四位二进制数对应一位十六进制数
所以二进制和十六进制间的转换非常容易
2to16:从小数点开始,分别向左、右按四位一组转换成对应的十六进制数字字符,最后不满四位的,补0
16to2:每位十六进制转化成四位二进制即可
位运算
因为计算机的本质还是各种电路集成起来的
想要完成复杂的运算首先要学会1+1等于几
那么计算机中最简单的小盒子可以完成的运算我们就叫位运算(门电路)
按位或 |
|两边只要有1结果就为1
0|0=0, 0|1=1, 1|0=1, 1|1=1
按位与&
&两边只要有0结果就为0
0&0=0, 0&1=0, 1&0=0, 1&1=1
按位异或^
^两边不同则为1,相同则为0
0&0=0, 0&1=1, 1&0=1, 1&1=0
所有的复杂运算都是通过位运算完成的
开始我们提到的1+1(二进制中)由于涉及到进位可以看成
1
+ 1
----------------
(1&1) (1^1)
也就是10
这样我们所有一位的二进制加法就掌握了(好耶!)
相比于+、-、*、/位运算速度更加的快(不是一个量级)
这是我们用位运算的主要原因
x>>1和x/2都是除以二的意思,但是速度差了好几倍
而且位运算也有一些神奇的用法(这里不详细说了)
计算一个二进制数中值为1的个数
先贴一下源码
x = (x & 0x55555555) + ((x >> 1) & 0x55555555);
x = (x & 0x33333333) + ((x >> 2) & 0x33333333);
x = (x & 0x0F0F0F0F) + ((x >> 4) & 0x0F0F0F0F);
x = (x & 0x00FF00FF) + ((x >> 8) & 0x00FF00FF);
x = (x & 0x0000FFFF) + ((x >>16) & 0x0000FFFF);
终于到正题了,呼呼~
想要算值为1的位数的数量有很多办法
(字符串处理啊,不断对2取余再除以2啊)
但是位运算是坠快滴!
首先!
我们的问题是数出二进制中值为1的个数
这个问题其实数据已经给我们答案了
因为这个二进制数上每一位记录的就是这一位上1的个数
(这当然是废话,1就是有1个1,0就是没有呗)
但是!
在分支思想中,我们已经完成了对小问题的解答!
(分治就是把一个大问题拆分成很多小问题,再把小问题拆成更小的问题)
我们要做的是求总体的数量,但是现在还存储在每一位上,我们要做的就是把他们加起来。
一个int型有四个字节
转换成二进制有32位(太长啦)
我们这里就拿两个字节做演示
假设
x=0B 1011 1101 0011 1100
(它的每一位上都是数字1的个数,废话!)
但是通过x = (x & 0x5555) + ((x >> 1) & 0x5555)
计算过程:
x & 0x5555:
1011 1101 0011 1100
& 0101 0101 0101 0101
\---------------------------------------
0001 0101 0001 0100
(x >> 1) & 0x5555 :
101 1110 1001 1110
& 0101 0101 0101 0101
---------------------------------------
0101 0100 0001 0100
我们可以看到位运算的好处是不会产生进位,所以看着很庞大的数据其实每两位所做的运算都是一样的。
对0x5555按位与留下了奇数位上的数字
而右移一位再对0x5555按位与留下了偶数位上的数字(右移了一位,所以结果也显示在奇数位)
(x & 0x5555) + ((x >> 1) & 0x5555):
0001 0101 0001 0100
+ 0101 0100 0001 0100
---------------------------------------
0110 1001 0010 1000
那么这步的运算有什么意义呢
刚刚我们每一位放的1的个数被拿出来了!
加号左边奇数位上的数字保存着奇数位1的个数
而加号右边奇数位上的数字保存着偶数位1的个数
这样一加每两位二进制数存储的就是这两位上1的个数(质的飞跃!)
与原数对比也可以看到
10 11 11 01 00 11 11 00(原来)
01 10 10 01 00 10 10 00(计算后)
1 2 2 1 0 2 2 0(每两位转换成十进制)
计算后每两位代表原数分别存储着1,2,2,1,0,2,2,0个1
即相邻 2 位中 1 的个数
(因为数据会越来越小所以不用担心放不下)
那么!
我们需要做的就是重复这么做,直到整个数代表每一位上1的个数
第二步
x=0110 1001 0010 1000(现在)
x = (x & 0x3333) + ((x >> 2) & 0x3333)
计算过程:
x & 0x3333:
0110 1001 0010 1000
& 0011 0011 0011 0011
\---------------------------------------
0010 0001 0010 0000
(x >> 2) & 0x3333:
01 1010 0100 1010
& 0011 0011 0011 0011
---------------------------------------
0001 0010 0000 0010
(x & 0x3333) + ((x >> 2) & 0x3333):
0010 0001 0010 0000
+ 0001 0010 0000 0010
---------------------------------------
0011 0011 0010 0010
即计算相邻 4 位中 1 的个数
与原数对比也可以看到
0110 1001 0010 1000(原来)
0011 0011 0010 0010(计算后)
3 3 2 2(每四位转换成十进制)
计算后每四位代表原数分别存储着3,3,2,2个1
同理后面的计算也是这样
原数的变化过程为
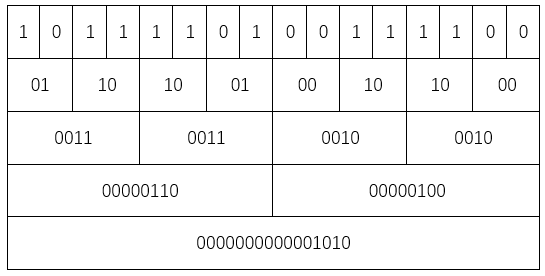
最后
x=0B0000000000001010=10
即共有10个1,4个字节的也同理
结束!



 浙公网安备 33010602011771号
浙公网安备 33010602011771号