CF1491G - Switch and Flip

CF1491G - Switch and Flip

题目大意

有\(n\)个硬币，编号\(1-n\)，第\(i\)个位置上当前放了编号\(a_i\)的硬币

每次交换\((a_i,a_j)i\ne j\)，且将硬币\(a_i,a_j\)翻转

求方案使得最终使得\(a_i=i\)且每个硬币恰好为原先方向

\(n\ge 3\)，方案步数\(\leq n+1\)

分析

显然要先对于\(a_i\)求出置换环，步数\(\leq n+1\)说明

1.general的情况可以用\(n\)步解决\(n\)个点

2.存在至多一个特殊情况要\(n+1\)步

手玩发现我们无法\(n\)步解决一个大小为\(n\)的环

但是如果环上恰好已经有两个硬币被翻过，那么可以

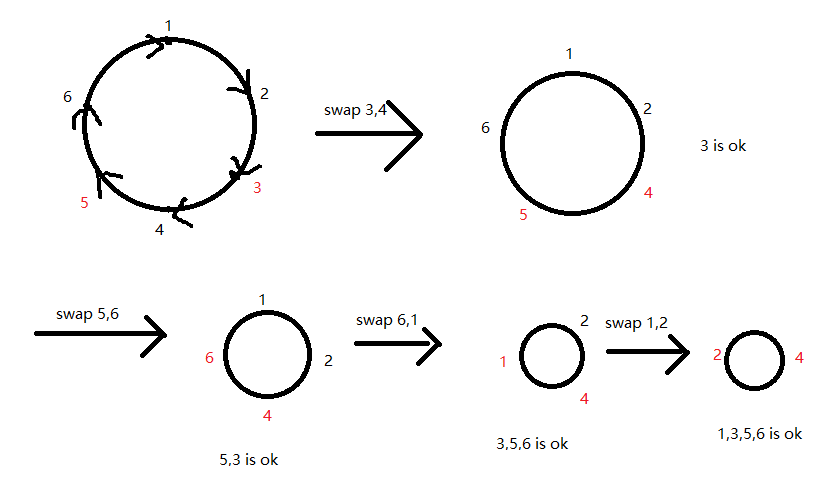
图上点表示硬币编号，箭头所指是这个硬币应该在的位置

我们从一个已经翻转的点开始，不断交换\(i,a_i\)上的硬币，会将\(a_i\)移动到到应该在的位置上

同时下一个位置被翻转

不断进行这个操作，直到这个点消去了半边环，遇到了下一个点也是被翻过的点

此时再从下一个点开始将环的另外半边消去

那么考虑如何让一个环有两个已经翻转的点

假设提取出了\(c\)个环，我们可以先尽量成对匹配两个环

通过一次跨过环的交换操作合并两个大小\(x,y\)的环，同时生成两个翻转点

然后进项上面的操作，需要\(x+y-1\)次，恰好一共\(x+y\)次

那么对于最后剩下的一个环

1.如果前面已经有环被匹配过

那么随便选择一个当前\(a_i=i\)的自环与其合并即可

2.整个图为一个大环

先通过交换\(1,a_1\)将\(a_1\)弹出，然后\(a_1\)再和环上另外一个元素交换

此时\(a_1\)变成未翻转状态，环又并成一个环+2个翻转点

const int N=2e5+10,INF=1e9+10;

int n;
int a[N],vis[N],b[N],c;

int X[N],Y[N],C,col[N];
void Swap(int x,int y){
	X[++C]=x,Y[C]=y;
	swap(a[x],a[y]),col[a[x]]^=1,col[a[y]]^=1;
}
void Solve(int i){ 
	while(!col[a[i]]) i=a[i];
	while(!col[a[a[i]]]) Swap(i,a[i]);
	i=a[i];
	while(i!=a[i]) Swap(i,a[i]);
}

int main(){
	n=rd();
	rep(i,1,n) a[i]=rd();
	rep(i,1,n) if(!vis[i]) {
		for(int j=i;!vis[j];j=a[j]) vis[j]=1;
		b[++c]=i;
	}
	for(int i=1;i<c;i+=2) {
		Swap(b[i],b[i+1]);
		Solve(b[i]);
	}
	if(c&1) {
		if(c==1) {
			int t=a[1];
			Swap(1,a[1]),Swap(t,a[1]);
			Solve(i);
		} else {
			rep(i,1,n) if(a[i]==i) {
				Swap(i,b[c]);
				Solve(i);
				break;
			}
		}
	}
	printf("%d\n",C);
	rep(i,1,C) printf("%d %d\n",X[i],Y[i]);
}