斜率优化学习笔记
题解并不是特别详细 , 代码可能会有细节问题 ,题目排列比较诡异
方法总结:
一、列出暴力dp的式子 用\(dp[i]=dp[j]....\)
二、找出里面的量,通常分三种:
1只与\(i\)有关
2.只与\(j\)有关的
3.对于同时与\(i,j\)有关的
三、固定 \(i\) ,对于\(x,y\)属于\(j\)的范围且 \(y \leq x\) ,设\(x\)比\(y\)更优,列出不等式,分离分母和分子的量
四、确定询问和加点的单调性 , 考虑单调队列还是二分之类的
T1 : MAX Average Problem - HDU 2993
当我们枚举右端点j时
有 $ sum_r , r $ 均递增
这时我们可以维护一个 斜率递增的 下凸包
(你可以画个图理解一下,事实上 上凸包时其中间的点一定不会更新答案)
然后就是查询
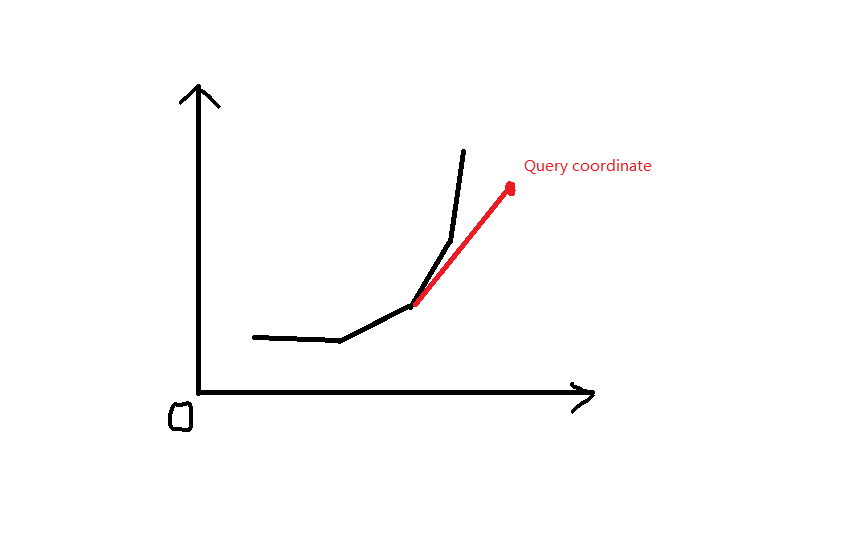
对于每一次插叙 , 并不具有单调性
(即不能使用单调队列去点)
所以要用单调栈+二分找到第一个如下图的点
int n,m;
int a[N];
int A[N],B[N],top;
int main(){
n=rd(),m=rd();
rep(i,1,n) a[i]=rd()+a[i-1];
double ans=0;
rep(i,m,n){
while(top>1&&1ll*(B[top]-B[top-1])*(i-m-A[top])>1ll*(a[i-m]-B[top])*(A[top]-A[top-1])) top--;
A[++top]=i-m;
B[top]=a[i-m];
int l=2,r=top-1,res=top;
while(l<=r){
int mid=(l+r)>>1;
if((1ll*B[mid+1]-B[mid])*(i-A[mid])>1ll*(a[i]-B[mid])*(A[mid+1]-A[mid])) res=mid,r=mid-1;
else l=mid+1;
}
//cout<<res<<endl;
ans=max(ans,1.0*(a[i]-B[res])/(i-A[res]));
}
printf("%.2lf\n",ans);
}
T2 : 羊羊列队
题目大意:
有一群羊可以随意排列,排列后分成m组,求每组之中高度差的总和的平方的最小值
例如队列中共有t只羊,高度依次为A1,A2……,At。那么不整齐度为:(|A1-A2|+|A2-A3|+……+|At-1-At|)2。即相邻两只羊高度差之和的平方。
样例:
Input :
4 2
4 1 3 2
Output
2
样例解释1 , 2 ; 3 , 4
其实就是一个模板题 , 将高度sort后转移
令\(dp[i][j]\)表示前\(i\)只羊,已经分了\(j\)组
对于每个\(o\)的已知量 $w=dp[o][j-1]+a[o+1]*a[o+1] $
对于每个\(i\)的已知量 $b=a[i]*a[i] \( 同时关系到\)i,o$的量 \(k=-2* a[i]*a[o+1]\)
(这里我们给出详细的推导过程,以后的题可能就不给了)
对于一个\(i\)
我们设\(x\)比\(y\)更优且\(y \leq x\),则有
可以看到式子里的量都是递增的
所以直接维护 \(w/k\) 递减
每次将大于\(2 \cdot a[i]\)的斜率去除
用单调队列!
int n,m;
ll a[N],dp[N][M];
ll A[N],B[N];
int L,R;
bool ed;
// dp[i][j]= min(dp[o][j-1]+(a[i]-a[o+1])*(a[i]-a[o+1]) ) ( 0<=o<i )
// w = dp[o][j-1]+a[o+1]*a[o+1]
// k = - 2* a[i]*a[o+1]
// b = a[i]*a[i]
// 维护 w/k 递减
// 每次将 大于 2*a[i] 的斜率去除
int main(){
n=rd(),m=rd();
rep(i,1,n) a[i]=rd();
sort(a+1,a+n+1);
memset(dp,63,sizeof dp),dp[0][0]=0;
rep(j,1,m) {
L=1,R=0;
rep(i,j,n) {
ll w=dp[i-1][j-1]+a[i]*a[i];
while(L<R && (B[R]-B[R-1])*(a[i]-A[R])>=(w-B[R])*(A[R]-A[R-1]) ) R--;
A[++R]=a[i];
B[R]=w;
while(L<R&&(B[L+1]-B[L])<=2*a[i]*(A[L+1]-A[L])) L++;
dp[i][j]=B[L]-2*a[i]*A[L]+a[i]*a[i];
}
}
printf("%lld\n",dp[n][m]);
}
基本上斜率优化的整个程序就是这样了
T3 : 斜率
题目描述:
平面中有 n 个点 (xi,yi) ,有 m 条直线,斜率 k 已经确定,需要在给定的 n 个点中,选出一个点 (x,y) ,使得 kx+y 最大。
真正的模板题,不想多讲
注意维护时先构造单调性!
const int N=1e5+10,K=20;
int n,m;
struct node{
ll x,y;
bool operator < (const node &__) const {
if(x^__.x) return x<__.x;
return y<__.y;
}
}p[N],A[N];
ll ans[N];
ll X[N],Y[N],L=1,R;
int main(){
n=rd(),m=rd();
rep(i,1,n){
ll x=rd(),y=rd();
p[i]=(node){x,y};
}
rep(i,1,m) A[i]=(node){rd(),i};
sort(p+1,p+n+1),sort(A+1,A+m+1);//构造单调性
rep(i,1,n){
while(L<R&&(p[i].y-Y[R])*(X[R]-X[R-1])>=(Y[R]-Y[R-1])*(p[i].x-X[R]) ) R--;
X[++R]=p[i].x,Y[R]=p[i].y;
}
rep(i,1,m){
while(L<R&&(Y[L+1]-Y[L])>=-A[i].x*(X[L+1]-X[L])) L++;
//cout<<A[i].x<<' '<<X[L]<<' '<<Y[L]<<endl;
ans[A[i].y]=A[i].x*X[L]+Y[L];
}
rep(i,1,m) printf("%lld\n",ans[i]);
}
T4: USACO - 土地征用 Land Acquisition
开始考虑更优的dp设计
首先注意到对于两个矩形\(i,j\),若\(x_i<=x_j , y_i<=y_j\)
则我们可以认为覆盖了\(j\)就一定覆盖了\(i\)
当我们把这些可以被覆盖的矩形去掉后,一定就能得到一个
\(x_i\)递增\(y_i\)递减的序列(真的很显然)
接下来我们就能将\(n\)块土地分成一段段去购买了,而且买连续的一段一定是最优的
剩下的就和上面讲的步骤一样
int n,m;
struct node{
int x,y;
bool operator < (const node __) const {
if(x!=__.x) return x<__.x;
return y>__.y;
}
}A[N];
// s - Que(j) + i * j
// rep(i,1,n) dp[i]=min(dp[j-1]+bj*ai)
// dp[x-1]+bx*ai<=dp[y-1]+by*ai
// (dp[x-1]-dp[y-1])/(by-bx) <= a[i]
// 维护一个下凸包
ll X[N],Y[N];
int L=1,R;
ll dp[N];
int ma[N];
int main(){
n=rd();
rep(i,1,n) A[i].x=rd(),A[i].y=rd();
sort(A+1,A+n+1);
drep(i,n,1) ma[i]=max(ma[i+1],A[i].y);
int t=0;
rep(i,1,n) if(ma[i+1]<A[i].y) A[++t]=A[i];
sort(A+1,A+t+1);
rep(i,1,n=t){
while(L<R&& 1ll*(Y[R]-Y[R-1])*(A[i].y-X[R]) < 1ll*(dp[i-1]-Y[R])*(X[R]-X[R-1]) ) R--;
X[++R]=A[i].y;
Y[R]=dp[i-1];
while(L<R&&(Y[L+1]-Y[L]) <=1ll*A[i].x *(X[L]-X[L+1]) ) L++;
dp[i]=Y[L]+1ll*X[L]*A[i].x;
}
printf("%lld\n",dp[n]);
}
T5 : USACO - 16FEB 再探圆形谷仓
注意只能顺时针走!
这题的\(dp\)方程式略显复杂
首先要维护从那个点建第一个谷仓
转移
我们要开两个数组维护这个\(distance-sum\)
一个\(sum[i]=\sum i*pos[i] ,a[i]=\sum pos[i]\)
则有$ distance-sum(i,j) = (sum[j]-sum[i]) - i*(a[j]-a[i])$
其实挺好理解的对吧
这样复杂度是 \(O( n^3 \cdot log(n) )\)
然后优化和上面一样自己推一下
哦,还有一个细节,就是选完m个点后后面肯能还有点,这里其实我们可以在\(st+n\)的地方放一个点,总共放\(m+1\)个点,就不用特判之类的了
int n,m;
ll a[N<<1],sum[N<<1];
ll dp[N<<1][M];
//dp[j][o]=min(dp[k][o-1]+sum[j-1]-sum[k]-(a[j-1]-a[k])*k
//dp[j][o]=min(dp[k][o-1]+sum[j-1]-sum[k]-a[j-1]*k - a[k]*k
// w=-sum[k]+a[k]*k+dp[k][o-1]
// k=-a[j-1]*k
// b= sum[j-1]
//(wx-wy)/(x-y) <= a[j-1]
// 维护一个递增的下凸包
ll A[N],B[N];
int L,R;
int main(){
n=rd(),m=rd();
rep(i,1,n) a[i]=a[i+n]=rd();
rep(i,1,n<<1) {
sum[i]=sum[i-1]+a[i]*i;
a[i]+=a[i-1];
}
ll ans=1e18;
rep(i,1,n) {
memset(dp,10,sizeof dp);
dp[i][1]=0;
rep(o,2,m+1) {
L=1,R=0;
rep(j,i+1,i+n) {
ll x=(j-1),y=-sum[j-1]+a[j-1]*(j-1)+dp[j-1][o-1];
while(L<R&&(B[R]-B[R-1])*(x-A[R]) > (y-B[R])*(A[R]-A[R-1])) R--;
A[++R]=x;B[R]=y;
while(L<R&&(B[L+1]-B[L]) <= a[j-1]*(A[L+1]-A[L])) L++;
dp[j][o]=-A[L]*a[j-1]+B[L]+sum[j-1];
//cout<<i<<' '<<j<<' '<<o<<' '<<dp[j][o]<<endl;
}
}
ans=min(ans,dp[i+n][m+1]);
//if(i==2) cout<<"#"<<dp[i+n][m+1]<<endl;
}
printf("%lld\n",ans);
}
[Ceoi2009]harbingers
题面:
给一个N个点的有根树,每条边有一个长度。从一个点出发,需要一个准备时间Si,有一个速度,表示每个单位路程需要的时间Vi。去根的路上,会经过其他点 j,可以选择花费Sj的时间准备后,按Vj的速度再次启程。
除了根节点,1号为根节点。
出发时没有速度,也需要花费时间来调整速度。
输入
第一行为一个整数N;
接下来N−1行,每行三个整数u,v,d,表示从编号为u的点到编号为v的点之间有一条边,长度为d;
接下来N−1行,第N+i行为两个整数Si+1,Vi+1
输出
输出N−1个整数,表示从编号为i+1的点到根节点的最小时间,每两个数之间用空格隔开。
样例
Input:
5
1 2 20
2 3 12
2 4 1
4 5 3
26 9
1 10
500 2
2 30
Output:
206 321 542 328
树上优化的鬼题
设\(dp[i]\)表示从\(i\)出发的最小时间
转移方程
\(dp[i]=dp[j]+ S[j] + (dis[i]-dis[j])*V[i]\)
仿佛很好优化的样子
其中\(dis[i]\)表示根到\(i\)路径总长,\(j\)是\(i\)的祖先
然后就是关键了
显然查询不具有单调性,必须二分
由于我们维护的单调栈是仅存储根到i路径上转移方案的
所以在子树之间会互相影响
如何避免这种影响呢?
对于当前的一个栈
我们用二分来寻找第一个可以维护单调性的点p
将其用当前方案替换并且更改top,同时记录被修改的点和原来的top
这里我们就在保证复杂度的前提下保留了栈内原来的点
(直接一个个退出栈再放进辅助数组里会让复杂度退化到\(n^2\))
递归结束时,我们一个个还原栈的情形,最后就能找到原来的样子
注意两次二分的细节很多
int n,m;
ll S[N],V[N];
struct Edge{
int to,nxt;
ll len;
}e[N<<1];
int head[N],ecnt;
void AddEdge(int u,int v,int len){
e[++ecnt]=(Edge){v,head[u],len};
head[u]=ecnt;
}
#define erep(u,i) for(int i=head[u];i;i=e[i].nxt)
// dp[u]= min( dp[fa] + s[u] + (dis[u]-dis[fa]) * v[u]) )
// dp[u]= min( dp[fa] + s[u] + dis[u]*v[u] - dis[fa] * v[u] )
// w=dp[fa]
// k=-dis[fa]*v[u];
// b=dis[u]*V[u]+s[u]
//(dp[x]-dp[y])/(dis[x]-dis[y]) <= V[u]
//维护一个递增的凸包
ll dp[N];
ll dis[N];
struct node{
ll x,y;
}stk[N];
int top;
int binary_search(int x){
int l=1,r=top-1,res=top;
while(l<=r){
int mid=(l+r)>>1;
if((stk[mid+1].y-stk[mid].y)>(long double)x*(stk[mid+1].x-stk[mid].x)) res=mid,r=mid-1;
else l=mid+1;
}
return res;
}
int Insert(int u){
if(top<2) return top+1;
int l=2,r=top,res=1;
while(l<=r){
int mid=(l+r)>>1;
if((long double)(stk[mid].y-stk[mid-1].y)*(dis[u]-stk[mid].x) <= (long double)(dp[u]-stk[mid].y)*(stk[mid].x-stk[mid-1].x) ) res=mid,l=mid+1;
else r=mid-1;
}
return res+1;
}
void dfs(int u,int f){
int p=Insert(u);
int t=top;
node x=stk[p];
top=p,stk[p]=(node){dis[u],dp[u]};
erep(u,i) {
int v=e[i].to;
if(v==f) continue;
dis[v]=dis[u]+e[i].len;
int t=binary_search(V[v]);
dp[v]=S[v]-stk[t].x*V[v]+stk[t].y+dis[v]*V[v];
dfs(v,u);
}
top=t,stk[p]=x;
}
int main(){
n=rd();
rep(i,2,n){
int u=rd(),v=rd(),c=rd();
AddEdge(u,v,c),AddEdge(v,u,c);
}
rep(i,2,n) S[i]=rd(),V[i]=rd();
dfs(1,0);
rep(i,2,n) printf("%lld",dp[i]),putchar(i==n?'\n':' ');
}
终极应用:COCI 2012/2013 contest#2 Inspektor 市场监控
这个原题着实不好找
题面:
S镇上的自由市场开业了。自由市场一共有N个摊位,会有不同的小贩来这里做买卖。身为自由市场的监管员,小C会不定时的抽查一些摊位的营业状况。一个小贩来到自由市场做生意需要以下信息(以下的时间都以S镇自由市场开业的那天作为起点计时):
T – 表示他是在自由市场开业后第T天来到自由市场做生意的;
K – 表示他在K号摊位做生意;
Z – 表示他从入驻的第二天开始每天的利润(又是生意不景气也可能亏损,所以Z可能为负)
S – 表示他一开始的拥有的财富(有些人是欠着债来做生意的,所以S可能为负)
如果一个摊位已经有人在做生意了,那么当有新的小贩来的时候,那个原来的小贩就会自动退出自由市场。一个小贩除非到退出自由市场,否则他拥有的财富就会每天以Z的速度增长或减少。
而小C监管自由市场也需要一些信息:
T – 表示他是在自由市场开业后第T天进行的检查;
A、B – 表示他将检查摊位编号在[A,B]的小贩目前的拥有的财富,并且记录下其中财富最大的一位的财富。
由于小C总是在当天自由市场闭市之后才去检查,所以小贩当天的收入也算在拥有的财富之内。
请你帮小C算算账,他每一次检查记录下来的最大财富值为多少。
输入
第一行包括2个正整数N,M,分别表示摊位的数量,以及事件的数量。
接下来M行,每行表示一个事件,第一个数字表示事件的类型,即小贩入驻自由市场
1 T K Z S
或小C进行检查:
2 T A B
给出的事件是按照时间顺序给出的。从S镇自由市场开业以来的每一天,最多发生一个事件,也就是说,每个事件中的T是严格递增的。
输出
对于每一次小C的检查,都要输出目前在他检查的范围内小贩拥有的财富值的最大值。如果检查范围内的所有摊位都没有小贩入驻,输出“nema”
样例
Input:
2 4
1 1 1 2 4
1 2 2 3 2
2 5 1 2
2 7 1 2
3 6
1 1 1 4 -2
1 2 2 2 6
2 3 3 1
2 4 3 1
1 5 3 -6 20
2 6 2 3
5 9
1 1 5 4 -5
2 2 3 5
1 3 4 6 9
2 4 1 2
1 6 2 2 3
2 8 2 1
1 9 4 0 17
2 10 5 5
2 11 1 4
Output:
12
17
8
10
14
-1
nema
7
31
17
分块正解!
分块维护动态的单调栈!
这题有点特殊
T是递增出现的,你可以二分,也可以将栈的顶弹出来查询(代码里有讲)
斜率优化的式子我就不讲了
我们可以先将\(S\)减去\(T*Z\)方便处理
对于每个块内
我们需要维护一个单调性方便加点
但显然题目中的\(S,Z\)不具有单调性
这时我们就要构造单调性
对于\(S_i,S_j,Z_i,Z_j\)
若\(S_i>=S_j , Z_i>=Z_j\)
那我们显然不需要考虑\(j\)了
所以我们又可以维护一个\(Z[i]\)递减,\(S[i]\)递增的序列
(插排你可会?)
每次更改后将整个块内的点全部重新维护一遍
然后就分块AC了啊!
const int N=1e5+10,SN=410;
// 令s[i]-=starttime*z[i];
// 则当前财富为 s[i] + T * z[i]
// 若i比j更优 s[i]+T*z[i] >= s[j]+T*z[j]
// (s[i]-s[j])/(z[j]-z[i]) >= T
// 维护了一个递减凸包
// 然后你会惊奇得发现这个T是递增的,不能直接单调队列(因为每次要去掉比T大的斜率)
// 然后你又会发现这个栈预处理后不会改变,你可以每次直接在栈里找到最后一个大于T的斜率,top--
// (奇葩)
// 显然s[i]与z[i]没有单调性
// 所以我们维护sort 以z[i]递减为第一关键字
// 对于一个z[i],如果比它大的z[i]出现了比它大的s[i]那么它一定没有用!
// 所以我们维护出了s[i]递增z[i]递减的一个顺序,就能搞了
int n,m,len;
int top[SN];
bool vis[N];
ll A[SN][SN],B[SN][SN];
int num[N],pos[N];
struct node{
ll x,y;
bool operator < (const node &__) const {
if(x!=__.x) return x>__.x;
return y>__.y;
}
ll Get(int t){ return y+t*x;}
} a[N];
inline void Upd(int p,ll S,ll Z){
int p1=p/len;
vis[p]=1;
a[p]=(node){Z,S};
reg int now=pos[p];
while(now>p1*len && a[num[now]]<a[num[now-1]]){
swap(pos[num[now]],pos[num[now-1]]);
swap(num[now],num[now-1]);
now--;
}
while(now<(p1+1)*len-1 && a[num[now+1]] < a[num[now]]){
swap(pos[num[now]],pos[num[now+1]]);
swap(num[now],num[now+1]);
now++;
}
reg ll ma=-1e18;
top[p1]=0;
rep(i,max(1,p1*len),min(n,(p1+1)*len)) if(vis[num[i]] ) {
if(ma>=a[num[i]].y) continue;
ma=a[num[i]].y;
while(top[p1]>1 && (long double)(B[p1][top[p1]]-B[p1][top[p1]-1])*(A[p1][top[p1]]-a[num[i]].x)<(long double)(a[num[i]].y-B[p1][top[p1]])*(A[p1][top[p1]-1]-A[p1][top[p1]])) top[p1]--;
B[p1][++top[p1]]=a[num[i]].y;
A[p1][top[p1]]=a[num[i]].x;
}
}
inline ll Que(int l,int r,int t){
int p1=l/len,p2=r/len;
//cout<<"Que "<<l<<' '<<r<<' '<<p1<<' '<<p2<<endl;
reg ll res=-1e18;
if(p1==p2) {
rep(i,l,r) if(vis[i]) res=max(res,a[i].Get(t));
return res;
}
rep(i,l,(p1+1)*len-1) if(vis[i]) res=max(res,a[i].Get(t));
rep(i,p1+1,p2-1) {
if(!top[i]) continue;
while(top[i]>1 && (long double)(B[i][top[i]]-B[i][top[i]-1]) <= (long double)t*(A[i][top[i]-1]-A[i][top[i]])) top[i]--;
res=max(res,B[i][top[i]]+t*A[i][top[i]]);
}
rep(i,p2*len,r) if(vis[i]){
//cout<<"res "<<i<<' '<<s[i]+z[i]*t<<endl;
res=max(res,a[i].Get(t));
}
return res;
}
int main(){
n=rd(),m=rd();
rep(i,1,n) a[i]=(node){(ll)-1e17,(ll)-1e17},pos[i]=i,num[i]=i;
len=min(n,(int)sqrt(n)+1);
rep(i,1,m){
int opt=rd();
if(opt==1){
int t=rd(),k=rd(),z=rd(),s=rd();
Upd(k,s-1ll*t*z,z);
} else {
int t=rd(),l=rd(),r=rd();
if(l>r) swap(l,r);
ll res=Que(l,r,t);
if(res<=-1e17) puts("nema");
else printf("%lld\n",res);
}
}
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号