状压dp【炮兵阵地】题解

毕竟我是蒟蒻，所以我只能写和常规做法，在注释里加上了一点自己的理解，不嫌弃可以康康~

 

题目描述

原题来自：NOI 2001

司令部的将军们打算在  的网格地图上部署他们的炮兵部队。一个  的地图由  行  列组成，地图的每一格可能是山地（用 H 表示），也可能是平原（用 P 表示），如下图。在每一格平原地形上最多可以布置一支炮兵部队（山地上不能够部署炮兵部队）；一支炮兵部队在地图上的攻击范围如图中黑色区域所示：

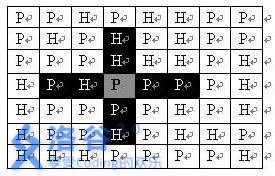
如果在地图中的灰色所标识的平原上部署一支炮兵部队，则图中的黑色的网格表示它能够攻击到的区域：沿横向左右各两格，沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。
现在，将军们规划如何部署炮兵部队，在防止误伤的前提下（保证任何两支炮兵部队之间不能互相攻击，即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内），在整个地图区域内最多能够摆放多少我军的炮兵部队。

输入格式

第一行包含两个由空格分割开的正整数，分别表示  和 ；
接下来的  行，每一行含有连续的  个字符(P 或者 H)，中间没有空格。按顺序表示地图中每一行的数据。

输出格式

仅一行，包含一个整数 ，表示最多能摆放的炮兵部队的数量。

样例

样例输入

5 4
PHPP
PPHH
PPPP
PHPP
PHHP

样例输出

6

 

 

#include<iostream>
#include<iomanip>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<cctype>
#include<algorithm>
#define ll long long
#define re register int
#define ull unsigned long long
#define mem(x,y) memset(x,y,sizeof(x))
#define sandom signed
#define mx 105
using namespace std;
int n,m,can_tot;//can_tot是用来合法情况的总数
char s[mx];
int cant[mx],allow[mx],cnt[mx];//cnt是当前行1的个数，sit是情况
int f[mx][mx][mx];//f[i][j][k]表示【前】i行，当前行状态为j，上一行状态为k，能放置的最多方案
//m<=10,n<=100
inline int read(){
	int x = 0;char c;bool f = false;
	while(!isdigit(c = getchar())){
		if(c == '-'){
			c = getchar(),f = true;
			break;
		}
	}
	do{
		x = (x << 3) + (x << 1) + (c & 15);
	}while(isdigit(c = getchar()));
	
	if(f == true) return -x;
	return x;
}
int lowbit(int x){
    return x & (-x);
}
int get_one_num(int x){
    int res = 0;
    while(x > 0){
        x -= lowbit(x),++ res;
    }
    return res;
}
void work(){
    //n行m列
    n = read(),m = read();
    for(re i = 1 ; i <= n ; ++ i){
        scanf("%s",s+1);
        for(re j = 1 ; j <= m ; ++ j){
            cant[i] <<= 1;//因为cant[]的初始值是0，因此让他一直左移没问题，然后如果有不能放的位置就加上1，继续该左移左移，该结束结束

            if(s[j] == 'H'){
                cant[i] |= 1;//也就是加上1
            }
            /*模拟一下：
            s:PPPHP
            so,cant[i] = {0 0 0 1 0}
            你已经注意到了，这么着是按照正序排的，所以一会用的时候要对应好
            */
        }
    }
    for(re i = 0 ; i < (1 << m) ; ++ i){//枚举每一种情况
        if((i & (i << 1)) == 0 && (i & (i << 2)) == 0){//如果他左边1列没有1，左边2列也没有1
            //因为我们是递推的，你画个图从0 -> 5就能知道了，只用判断他左边就行
            allow[++can_tot] = i,cnt[can_tot] = get_one_num(i);
        }
    }
    for(re i = 1 ; i <= n ; ++ i){//枚举第i行
        for(re j = 1 ; j <= can_tot ; ++ j){//枚举当前行状态
            for(re k = 1 ; k <= can_tot ; ++ k){//枚举上一行状态
                for(re l = 1 ; l <= can_tot ; ++ l){//枚举上上行状态
                    if((allow[j] & allow[k]) == 0 && (allow[j] & allow[l]) == 0 &&(allow[j] & cant[i]) == 0){
                        //这三种情况(上上行，上一行，当前行)都不冲突，而且当前行与地形也不冲突
                        f[i][j][k] = max(f[i][j][k],(f[i-1][k][l] + cnt[j]));
                        //+cnt[j]我来解释一下，这个的意思是说当前枚举的当前行状态j所拥有的1也就是放了的炮兵，上一行之前有了的加上当前行的情况新增的
                    }
                }
            }
        }
    }
    int final_ans = 0;
    for(re i = 1 ; i <= can_tot ; ++ i){//枚举当前行状态
        for(re j = 1 ; j <= can_tot ; ++ j){//枚举上一行状态
            //因为我们是递推，最后的答案都推过来了，又因为是三维，第一维肯定是最终推到了第n行，所以只需要循环当前行状态和上一行状态，并且不用判断合不合法，不合法不会影响
            final_ans = max(f[n][i][j],final_ans);
        }
    }
    printf("%d",final_ans);
}
sandom main(){
    work();
    return 0;
}