特征放缩 scaling

Feature scaling

主要有以下四种计算方法:

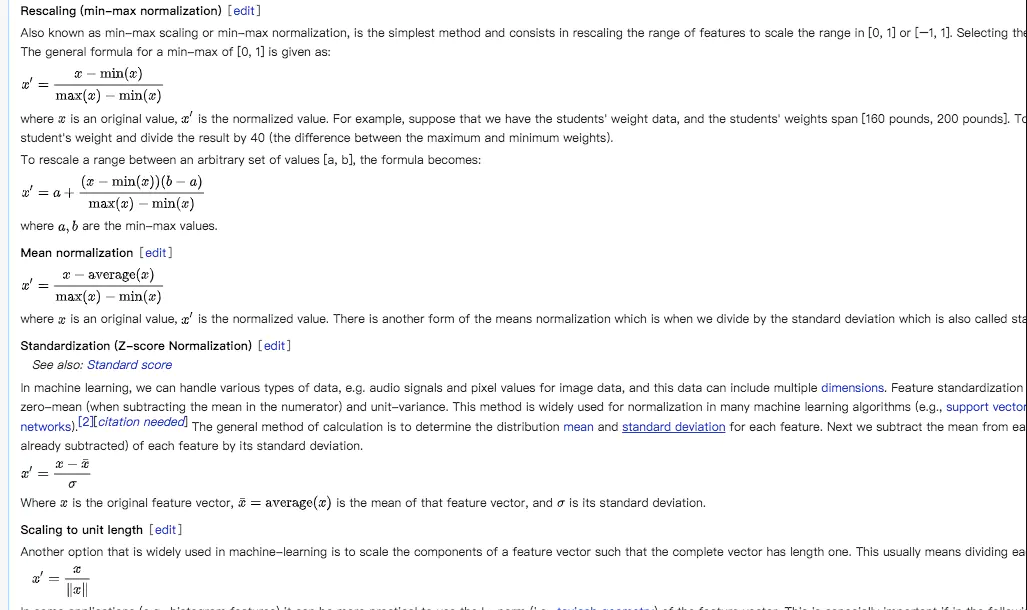
正如上图所示，实现的方法主要是Rescaling(min-max normalization)、Mean normalization、Standardization(z-score normalization有的地方叫做zero-mean normalization)和Scaling to unit length。

要说明的是对于归一化(normalization)(也有地方是说正则化，但是正则化应该是指regularization，到底是怎么翻译还是要根据具体情况看)和标准化(standardization)都是属于特征缩放(feature scaling)的方法，用于实现对数据的预处理。

这也算是历史遗留问题了，在kaggle中也提到Scaling vs. Normalization: What's the difference?。

文中是这样说的:

One of the reasons that it's easy to get confused between scaling and normalization is because the terms are sometimes used interchangeably and, to make it even more confusing, they are very similar! In both cases, you're transforming the values of numeric variables so that the transformed data points have specific helpful properties. The difference is that:

in scaling, you're changing the range of your data, while

in normalization, you're changing the shape of the distribution of your data.

正如文中所提到的，它们是一个意思。

实现方法：Scaling and Normalization | Kaggle

那么为什么要特征缩放？

1. 提升模型的准确性&统一权重

因为在机器学习中，如果某列数据极差很大（比如在预测房价的趋势的时候，比如有影响因素--房间面积，最大是上千，但又比如影响因素--房间数量最小1）这就会让模型感到迷惑，不利于机器学习模型的学习，所以需要对该列数据进行缩放。（将数据大小控制在一个合理的范围）。在随机梯度下降法中，特征缩放有时能加速其收敛速度。而在支持向量机中，他可以使其花费更少时间找到支持向量，特征缩放会改变支持向量机的结果。

2. 提高梯度下降算法的收敛速度

在使用梯度下降法求解最优化问题时，归一化/标准化数据后可以加快梯度下降的求解速度。

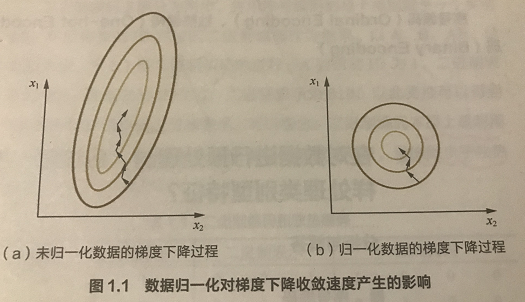
归一化(normalization)

针对一个数据维度的操作，将数据范围缩放至[0,1]或者[-1,1]。将数据按比例缩放，使之落入一个小的特定区间。在某些比较和评价的指标处理中经常会用到，去除数据的单位限制，将其转化为无量纲的纯数值，便于不同单位或量级的指标能够进行比较和加权。

Rescaling (min-max normalization)

举例来说明：

假设有一个数据集[120,180,90]，那么根据$x' = \frac{x-min(X)}{max(x)-min(x)}$可知，归一化的结果是:

$x1 = \frac{120-90}{180-90}=30/90=0.333 \\ x2 = \frac{180-90}{189-90}=1 \\ x3=\frac{90-90}{180-90}=0$

可以看出数据是在[0,1]的范围内的。

Mean normalization

还是以数据集[120,180,90]为例，根据$x'=\frac{x-mean(x)}{max(x)-min(x)}$，归一化的结果是:

$x1=\frac{120-130}{180-90}=-10/90=-0.1111 \\ x2 = \frac{180-130}{180-90}=50/90=0.556 \\ x3 = \frac{90-130}{180-90}=-40/90=-0.444$

数据的范围为[-1,1]，同时归一化数据之和是0。

Standardization

standardization也叫做-score 标准化(zero-mean normalization)，最常见的标准化方法就是Z标准化，也是SPSS中最为常用的标准化方法，spss默认的标准化方法就是z-score标准化。也叫标准差标准化，这种方法给予原始数据的均值（mean）和标准差（standard deviation）进行数据的标准化。经过处理的数据符合标准正态分布，即均值为0，标准差为1. 一般的计算方法是确定每个特征的分布均值和标准差。接下来从每个特征中减去平均值，将每个特征的值（平均值已被减去）除以其标准差。

z-score标准化方法适用于特征最大值和最小值未知的情况，或有超出取值范围的离群数据的情况。该种归一化方式要求原始数据的分布可以近似为高斯分布，否则归一化的效果会变得很糟糕。

Scaling to unit length

缩放特征向量的分量，使得整个向量的长度为1。这通常意味着将该向量的每个元素除以向量的欧几里德长度。

哪些算法需要用到特征缩放

通过梯度下降法求解的模型需要进行特征缩放，这包括线性回归（Linear Regression）、逻辑回归（Logistic Regression）、感知机（Perceptron）、支持向量机（SVM）、神经网络（Neural Network）等模型。此外，近邻法（KNN），K均值聚类（K-Means）等需要根据数据间的距离来划分数据的算法也需要进行特征缩放。主成分分析（PCA），线性判别分析（LDA）等需要计算特征的方差的算法也会受到特征缩放的影响。

决策树（Decision Tree），随机森林（Random Forest）等基于树的分类模型不需要进行特征缩放，因为特征缩放不会改变样本在特征上的信息增益。

言外：normalization, standardization, regularization

normalization(归一化), standardization(标准化), regularization(正则化)还是有区别的，但是主要的区别还是两大类。

通过前面的论述可以知道normalization和standardization是差不多的，都是把数据进行前处理，从而使数值都落入到统一的数值范围，从而在建模过程中，各个特征量没差别对待。

normalization一般是把数据限定在需要的范围，比如一般都是[0,1]，从而消除了数据量纲对建模的影响。
standardization 一般是指将数据正态化，使平均值0方差为1，数据范围是[-1,1].
因此normalization和standardization 是针对数据而言的，消除一些数值差异带来的特种重要性偏见。经过归一化的数据，能加快训练速度，促进算法的收敛。

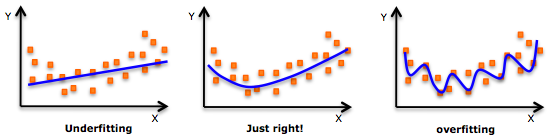
而regularization是在cost function里面加惩罚项，增加建模的模糊性，从而把捕捉到的趋势从局部细微趋势，调整到整体大概趋势。虽然一定程度上的放宽了建模要求，但是能有效防止over-fitting的问题(如图，来源于网上)，增加模型准确性。因此，regularization是针对模型而言。