线性回归方程的理解

什么是一元线性回归方程呢？这篇文章提出了概念，并且还利用正态分布与cost function的表达式的关系。

文中引言也通俗地提出了什么是回归——本质上就是确定一种非确定的关系。

任何一个合格的大学生，都肯定在高中数学的《选修2-3》中接触过回归(regression)，在那个时候我们就知道，回归分析就是给了一些数据点，根据这些数据点画一条直线，然后我们就根据这条直线去做预测。所有学统计的人也应该都会有一种感觉，就是说，统计一定程度上，破坏了数学的严谨性。出现这一条鄙视链的原因是，统计研究的是一种非确定性关系。

作为一个学数学的人，在没接触统计学之前，最烦的就是“不确定”。一加一等于几，你不能说它又是2，又是3。抽象一层来说，就有点“函数”的意思。在初中第一次接触函数就知道，给定一个自变量 ，你必须要告诉我确定的 是多少。这就是确定性关系。它不打马虎眼的，结果是确定的。

那么为什么说统计“不严谨”呢？比方说你研究一个人身高与体重的联系，这个时候，你告诉我一个人的身高 ，我是没有办法告诉你一个确定的体重 的。出现这样的问题的原因归因于世界的概率和未知。换句话说，世界上任何一个事情，都是有自己的概率分布的。比如说“太阳不可能从西边升起”这句话，实际上暗含的意思是“太阳从西边升起的概率为0”（当然细究一下这句话确实也不够严谨，因为概率为0并不代表不会发生）。所以只能说使用统计去找到某一个“最有可能发生的地方”，然后认为这个“概率最大”的地方就是我们要的结果。比如说我告诉你我身高是184cm，那么通过统计，你可以认为我“最有可能”体重是75kg，那么一般来说，如果作预测，你可能就会说，你“预测”我是75kg。但是实际上不一定是75kg的。

那么回归分析是怎么回事呢？如果我知道对于每一个 都有一个确定的 ，那么就没统计什么事了。但是如果对于每一个 都有一个确定的 的概率分布，你就会发现坏事了。下面一个图展现了这个问题，也展现了具体的“非确定性关系”。

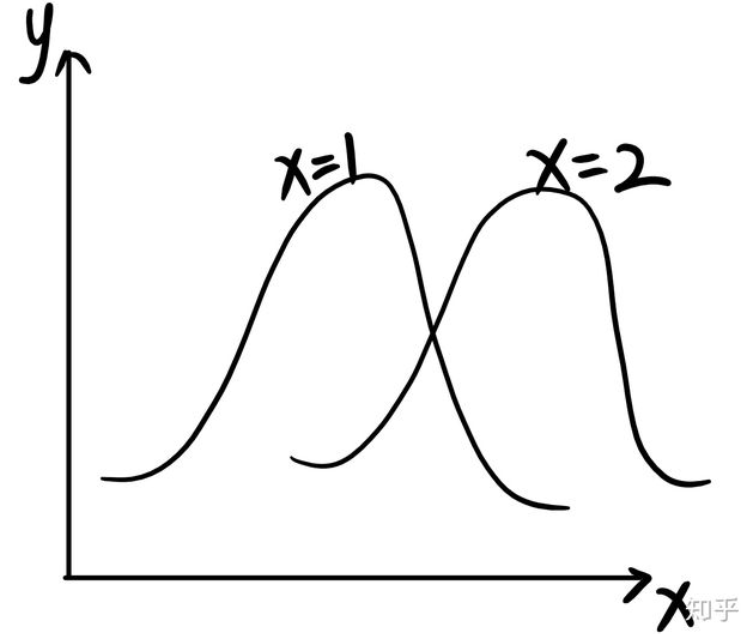
（对于每一个具体的x，都会有不同的概率分布，那么想给定一个确定的y就不可能了，因为在概率分布上的每一个值y都有可能是最终的结果。）

为了勾勒出这种“非确定性关系”，我们引入了相关分析和回归分析。相关分析就是很单纯的，研究两个变量之间的关系。我当然可以认为两个变量都是随机变量。但是回归分析，是要研究因果关系的。要求给定的 ，也就是“原因”，要明确。这会引出我们之后说的回归分析的三大基本假设之一。而回归分析，本质上，就是把可能概率最大的点给找出来，然后画在图上。

一开始我在想，为什么会有最小二乘法的应用，cost function可以去那么写，线性回归的依据又是什么……；

现在我可以想到的假设就是，依据极大似然估计可以构建出一个参数未知数学模型;

什么要假定为“正态分布”呢？除去正态分布的满足的比较好的一些性质以外，还有一个考虑是，它让回归“有办法”能够捕获到“概率最大”的点。下面的图就说明了这一点。

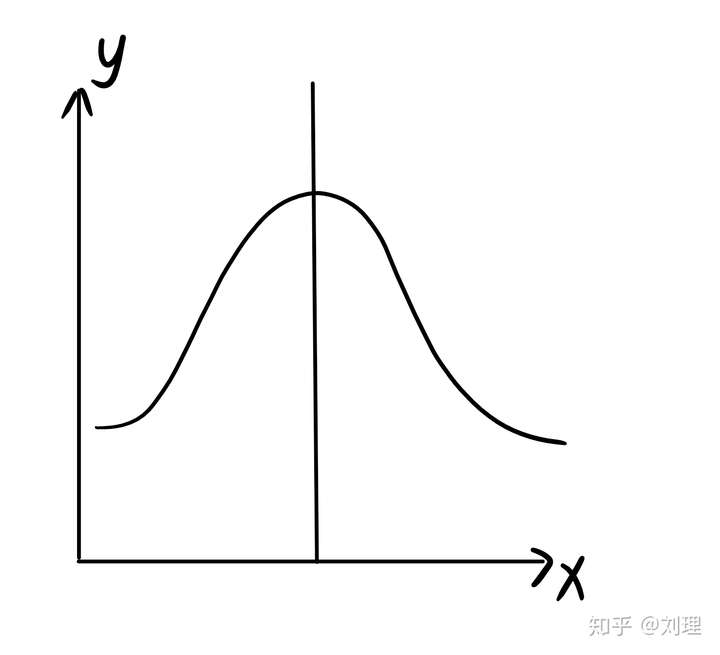
因为正态分布的期望值就正好落在最高处，也就是说，我们要求的E(y|x)对应的那个x值就正好是概率最大的点，符合我们的预期。（我记得看过一篇文章，文中说到依据大数定律，而正态分布又是生活中常见的一种模型）

依据概率论的知识，我们将自己预测的模型(其实我感觉就是概率密度的相乘，即P(x|\(\theta\)))相乘，因为这是概率的结果相乘，我们需要让结果尽可能的大，那就需要求导即可了。