机器学习笔记4

19. Recommender Systems

两种算法，一种是基于推荐内容的推荐算法，另一种是叫做协同过滤的推荐算法;

19.1 Content-based recommendations

这一节主要是以电影推荐为例进行讲解，我们要做的就是，根据用户已经评价过的电影分数来预测还没看的电影的评分。

在开始之前，先说明一些变量的声明问题：

• \(n_u\)表示用户的数量；

• \(n_m\)表示电影的数量；

• \(r(i,j)=1\)表示用户j评价了电影j；

• \(y^{(i,j)}\)表示用户j对电影i的评分(评分范围为0~5)；

---

如下图所示，“？”表示用户还没看的电影，也就是我们需要预测的数值，我们假设用两个feature来描述电影的情况，其中\(x_1\)衡量电影的爱情片程度，\(x_2\)衡量电影的动作片程度：

有了这些形象化的定义之后，再用向量的形式进行表示：

定义：\(x^i=\begin{bmatrix} x_0 \\ x_1 \\ x_2 \end{bmatrix}\)​​表示第i个电影的种类程度，其中\(i \in[1,n_u]\)​​，n=2，表示特征数。\(x_0\)​​还是一个恒等于1的偏移量。

对于每一个用户j，需要拟合一个参数\(\theta^j\)​(3*1的矩阵，会在下面讲到这个是怎么求的)，那么预测电影i的评分可以用：\((\theta^j)^Tx_i\)来表示。

---

有了上述的分析之后，再次重申一下符号的定义，以便能够表示出计算过程：

• \(n_u\)表示用户的数量；
• \(n_m\)表示电影的数量；
• \(r(i,j)=1\)表示用户j评价了电影j；
• \(y^{(i,j)}\)表示用户j对电影i的评分(评分范围为0~5)；
• \(\theta^j\)​​​表示用户j需要拟合的参数矩阵(也即观众对影片的喜爱程度)；
• \(\theta_k^j\)​​表示用户j需要拟合的第k参数的参数矩阵；
• \(x^i\)表示对于电影i的所有feature数值，也是一个矩阵；
• \(m^j\)表示用户j评价的电影数量；

以一个用户为例，参考线性回归的拟合过程可以得出我们Optimization Objective(regularization 项不包含偏移量)：

\(min\{\theta^j\}\;\frac{1}{2}\sum \limits_{i:r(i,j)=1}((\theta^j)^Tx_i-y^{(i,j)})^2+\frac{\lambda}{2}\sum\limits_{k=1}^n(\theta^j_k)^2\),其中\(i:r(i,j)=1\)​​​表示所有的i中r(i,j)=1的j。

那么对于全体的用户表示就是再添加一个求和符号即可：

\(min\{\theta^1,...,\theta^{n_u}\}\; \frac{1}{2}\sum \limits_{j=1}^{n_u}\sum \limits_{i:r(i,j)=1}((\theta^j)^Tx_i-y^{(i,j)})^2+ \frac{\lambda}{2}\sum \limits_{j=1}^{n_u}\sum \limits_{k=1}^n(\theta_k^j)^2\)​

有了Optimization Objective之后，剩下要做的就是梯度下降了：

19.2 Collaborative filering

这一节来讲解另一种推荐算法——协同过滤；

这种算法有一种很有趣的特性叫做特征学习，这种算法可以自行学习所需要的特征。

上面这句话是什么意思呢，还是看电影的这个问题：

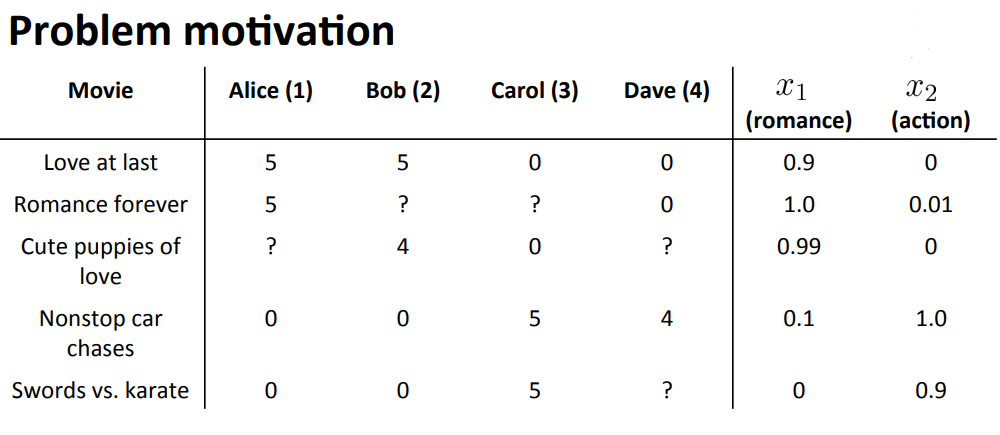
每个电影的romance程度和action程度都是由用户给出的，那么如果一开始并没有这两个属性，那么该如何判断影片的这两个属性呢?这就是协同算法要做的事情。

---

现在的问题变成了如下图所示的问题：

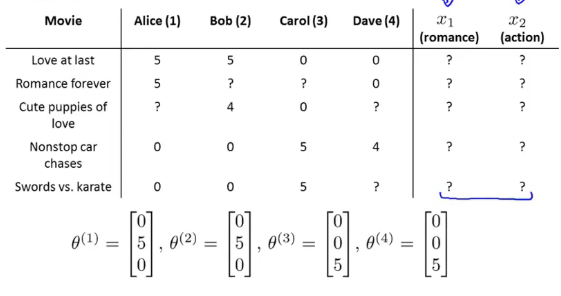
建立一个场景：我们不可能花重金去让每一个观众去看所有的电影，并根据电影的所具备的属性去打标签，也就是我们定义的\(x_i\)(这里就举两个属性的例子)​，这是不现实的。但是我们可以根据每一位观众对影片的评分，以及其对哪种系列的电影的热爱程度，通过这两个条件，便可以推断出观众所看电影所具备的属性程度(有点意识流了)。

定义\(\theta^i_j\)​表示第i个观众对\(x_i\)​类型影片的喜爱程度。

具体来说就是\(\theta^1=\begin{bmatrix} 0 \\ 5 \\ 0 \end{bmatrix}\)​​表示Alice用户对\(x_1\)类型(romance)的电影喜爱程度为5分，对\(x_2\)类型(action)的电影喜爱程度为0分。其他的以此类推。

通过上图中给出的\(\theta^j\)​，可以电影\(x^1\)​很有可能是爱情类的电影，因为Alice 和 Bob非常喜欢，那么由19.1中提到计算公式：\((\theta^j)^Tx^i=y^{(i,j)}\)​;

那么可以由\((\theta^1)^Tx^1=5,(\theta^2)^Tx^1=5,(\theta^3)^Tx^1=0,(\theta^4)^Tx^1=0\)​​​

得出\(x^1=[0\;1.0\;0]^T\)，其中\(x_1^1=1\)​​,这也就是说影片1的romance属性达到了1的程度。

---

那么类比于19.1中提到的Optimization Objective，那么Collaborative filtering的Optimization Objective就是：

\(min\{x^1,...,x^{n_m}\}\; \frac{1}{2}\sum \limits_{i=1}^{n_m}\sum \limits_{j:r(i,j)=1}((\theta^j)^Tx_i-y^{(i,j)})^2+ \frac{\lambda}{2}\sum \limits_{i=1}^{n_m}\sum \limits_{k=1}^n(x_k^i)^2\)

19.3 Collaborative filtering algorithm

这一节是对19.1和19.2中提出的计算方法来进行整合到一起。

这里提出一个非常有趣的想法，类似一个“先鸡后蛋还是先蛋后鸡”的问题，为了更好地拟合模型，可以不断地去迭代计算上述的两个式子，具体来说就是假设一开始有了\(\theta^j\)​，那么就可以估计出\(x^i\)​,进而再估计出新的\(\theta^i\)​，……就这样不断迭代最后达到收敛。

但是这样的方法由于迭代导致计算复杂，因此采用另外下面的方法来实现：

Minimizing \(x^i\) 和 \(\theta^j\) simultaneously

\(min\{(x^1,...,x^{n_m}),(\theta^1,...,\theta^{n_u})\}= \\ J(x^1,...,x^{n_m},\theta^1,...,\theta^{n_u}) \frac{1}{2}\sum \limits_{(i,j):r(i,j)=1}((\theta^j)^Tx^i-y^{(i,j)})^2+\frac{\lambda}{2}\sum \limits_{i=1}^{n_m} \sum \limits_{k=1}^n(x_k^i)^2+ \frac{\lambda}{2} \sum \limits_{j=1}^{n_u} \sum \limits_{k=1}^n (\theta^j_k)^2\)

需要说明的是：

• 这个式子在计算关于x的优化的话，关于\(\theta\)的regularization项就会没有，变成了19.1中的式子，同理，如果是最小化关于\(\theta\)的，那么公式就会变成19.2中说的式子。
• 这个式子不同于迭代时候的公式，其是不包含intercept term(\(x_0,\theta_0\))的，也就是说x和\(\theta\)​项都是n维向量，不是原来的n+1维向量了，因为在计算的过程中可以拟合恒为1的截距项的，前提是如果需要的话。

---

总结一下Collaborative filtering algorithm过程：

19.4 Vectorization： Low rank matrix factorization(低秩矩阵分解) & Other things with alogrithm

这一节主要讲如何向量化表示参数和如何推荐相关的产品。

---

首先是如何向量化表示参数：

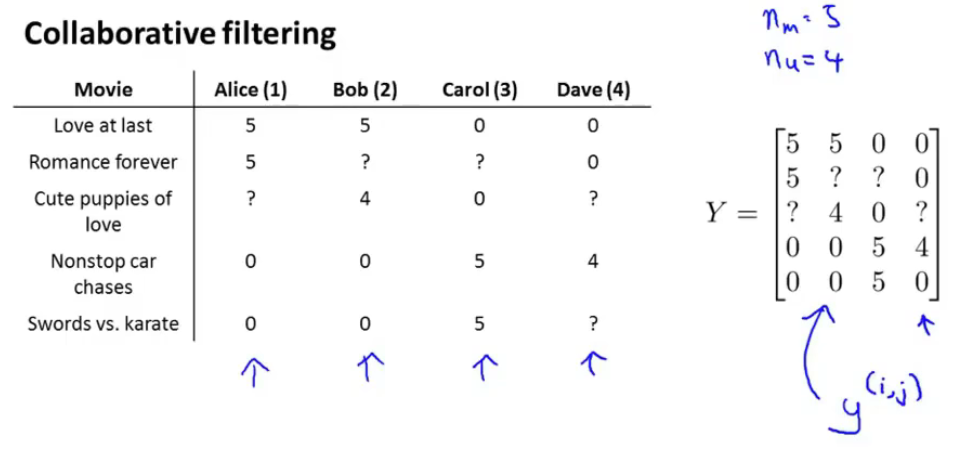
此时已经是表示出用户和电影的关系，用矩阵Y来表示，也叫做评分矩阵，\(y^{(i,j)}\)​就是我们以前定义的用户j对电影i的评分。

那么用参数表示出Y矩阵如下：

​

对于评分矩阵可以表示成两个矩阵的相乘，也就是\(X=\begin{bmatrix} (x^1)^T \\ (x^2)^T \\ ... \\ (x^{n_m})^T \end{bmatrix} \; \Theta= \begin{bmatrix} (\theta^1)^T \\ (\theta^2)^T \\ ... \\ (\theta^{n_u})^T \end{bmatrix} \; Y = \Theta X^T\)​

这个过程就叫做low rank matrix factorization。

低秩矩阵分解中低秩Low-rank怎么理解呢？

我尝试简单来概括就是，低秩就是矩阵的秩远小于行数或者列数，也就是线性相关比较强，矩阵中存在着大量的冗余信息，但是利用这种可以相互表示的性质，可以对缺失的数据进行补充，这就引出了一个新的名词——矩阵补全，也可以对数据进行提取特征。

那么矩阵分解的意思是什么呢？

先说一下低秩分解的目的：去除冗余，并且减少权值参数

方法：采用两个K*1的卷积核A和B，代表一个K*K的卷积核M(decompose the K convolutions into two separable convolutions of size 1 × K and K × 1)，那么 A*B 的元素就可以用于估计M中对应不可见位置的元素值，而A*B可以看做是M的分解，所以称作Matrix Factorization

原理：这是因为协同过滤本质上是考虑大量用户的偏好信息（协同），来对某一用户的偏好做出预测（过滤），那么当我们把这样的偏好用评分矩阵M表达后，这即等价于用M其他行的已知值（每一行包含一个用户对所有商品的已知评分），来估计并填充某一行的缺失值。若要对所有用户进行预测，便是填充整个矩阵，这是所谓“协同过滤本质是矩阵填充”。

那么，这里的矩阵填充如何来做呢？矩阵分解是一种主流方法。这是因为，协同过滤有一个隐含的重要假设，可简单表述为：如果用户A和用户B同时偏好商品X，那么用户A和用户B对其他商品的偏好性有更大的几率相似。这个假设反映在矩阵M上即是矩阵的低秩。

我会在【低秩分解】中详述这一部分。

(14条消息) 机器学习——低秩矩阵分解中低秩的意义、矩阵填补、交叉验证_manduner的博客-CSDN博客_低秩矩阵分解

低秩分解 - weilongyitian - 博客园 (cnblogs.com)

---

剩下需要讨论的就是如何推荐给用户相关的电影呢？

对于某一个电影i，我们需要通过算法找到一个特征矩阵\(x^i\),这个矩阵包含了可能难以理解的属性，但是能够很好地表示商品本身。

有了特征矩阵，那么如何判断电影i与电影j是相似的呢，其实也是很简单的，就是通过计算两个向量之间的距离\(||x^i-x^j||\)

19.5 Implementational detail: Mean normalization

这一节主要是讲解一个处理方法——Mean normalization。

---

要说这个方法在推荐系统中有什么用，那就需要用到一个例子来说明。

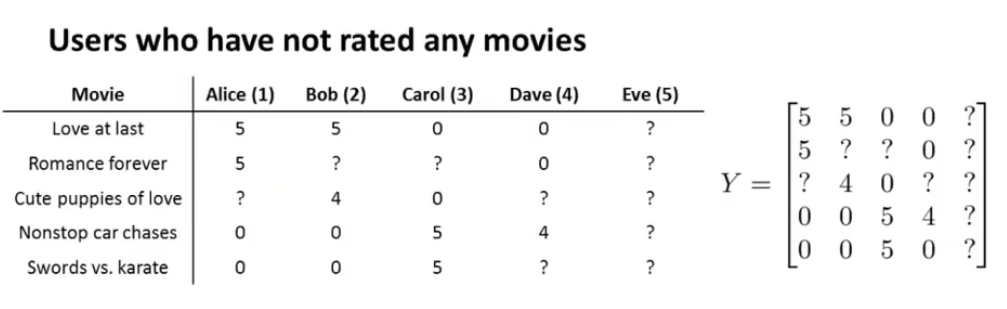
假设存在上图中的情况——有一位新观众Eve，这位观众并未对这个电影推荐系统中的电影进行评价，也就是说评分矩阵中的第5列的数值全是未知的，那么此时我们用19.3中提出的公式：

\(min\{(x^1,...,x^{n_m}),(\theta^1,...,\theta^{n_u})\}= \\ J(x^1,...,x^{n_m},\theta^1,...,\theta^{n_u}) \frac{1}{2}\sum \limits_{(i,j):r(i,j)=1}((\theta^j)^Tx^i-y^{(i,j)})^2+\frac{\lambda}{2}\sum \limits_{i=1}^{n_m} \sum \limits_{k=1}^n(x_k^i)^2+ \frac{\lambda}{2} \sum \limits_{j=1}^{n_u} \sum \limits_{k=1}^n (\theta^j_k)^2\)

对\(\theta^5\)求偏导，那么只有regularization项被最小化(因为r(i,j)=1都不满足)，其余的被看成常数被约去了，又因为要最小化，就导致\(\theta^5\)的每一个属性全是0，进一步导致系统没有办法给新来的观众Eve推荐任何一部影片。

这显然是不合适的。

---

出现的问题原因在于上述的处理方法使\(\theta^5\)​全部为0，为此需要对数据预处理——此时Mean normalization就出场了。

先对数据进行求均值：

\(\mu\)的第一个2.5来自(5+5+0+0)/4，第二个2.5来自(5+0)/2,......

那么就需要构建一个新的评分矩阵Y了，计算方法就是让原来的每个数值减去对应行的\(\mu\)：

在均值化之后，将其参数运行在上述的公式中，然后不同于一般的做法的是，最后的评分需要加上\(\mu_i\)​，即 \(y^{(i,j)}=(\theta^j)^Tx^i+\mu_i\)​​。

此时虽然Eve的\(\theta^5\)矩阵的数值还全是0，但是由于加上了均值，此时的便可以对该用户推荐了电影。

20. Large scale machine learning

这一大节主要是讲解在大数据(比如100亿)的前提下，如何在计算层面上提出进一步的优化策略。

20.1 Stochastic gradient descent

讲随机梯度下降算法之前，回顾一下原先在线性回归中使用过的梯度下降算法：

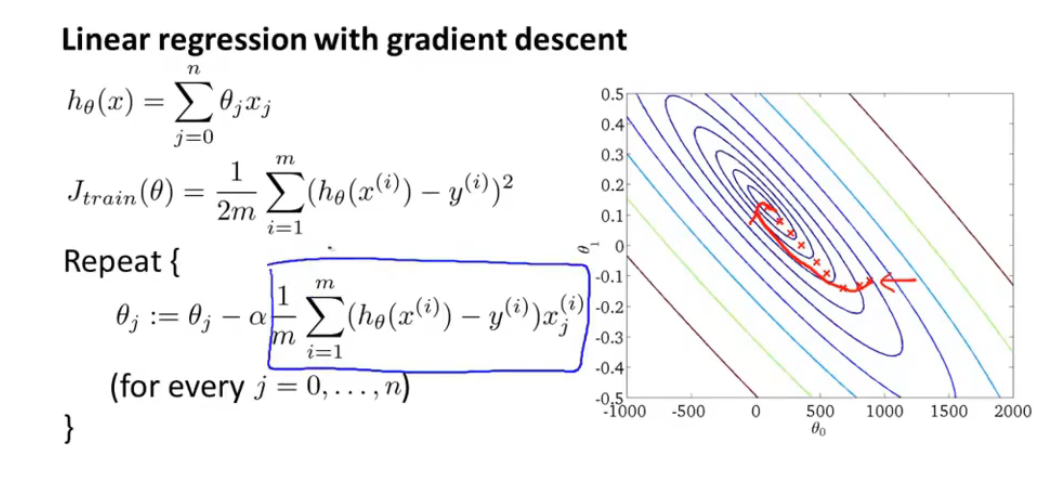
仔细观察可以看到，Repeat部分每次更新一个\(\theta_j\)​就需要将m个数据读入内存中，因此由于这样的处理方式，上述的梯度下降算法也在其他地方叫做——Batch gradient descent(为了比较方便，下面我将使用这个名称与Stochastic gradient descent做区别对比)。

因此没循环处理完m个数据一次，在图像中就会移动一次，对于数量集很大的情况下，情况并非乐观。

---

那么Stochastic gradient descent是怎么做的呢？

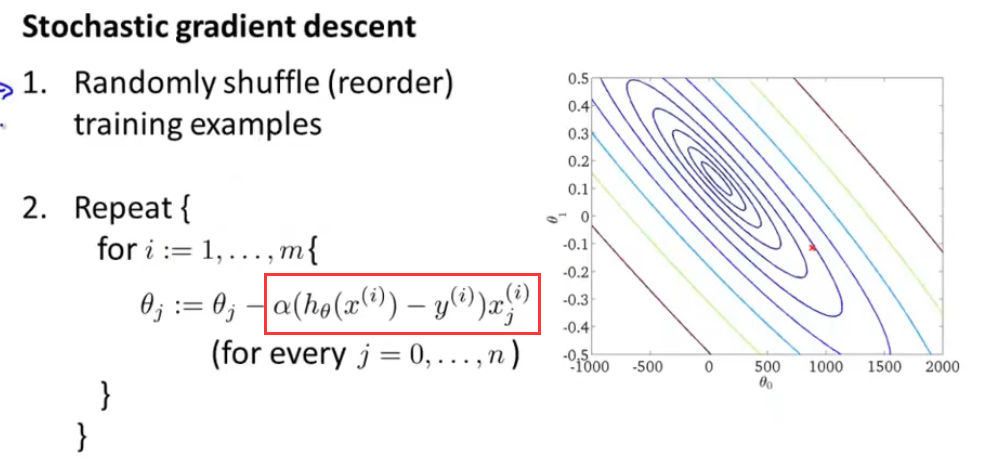
首先将数据全部随机打乱(其实如果不是刻意排序，整个数据集应该是乱的)，那么剩下的就是在Repeat部分不同了。

根据上图可以看出，对于内循环，只需要对数据集中的一个数据进行拟合，就可以达到梯度下降的目的，也就是说，如果将这个数据集遍历一遍，那么在图像中一共移动了m次，并且逐渐靠近全局最优解，并且相比于Batch gradient decent，不用一次性去处理m个数据了。

随机梯度下降的图像如下图洋红色的路径所示：

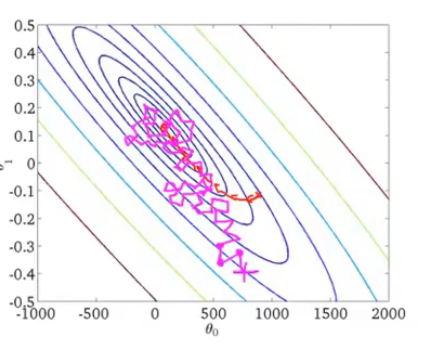
虽然收敛的路径不同，但是在速度上是比Batch gradient descent 好多了，路径的移动成本也更低。

20.2 Mini-batch gradient descent

目前来说已经学习了两种梯度下降的处理方法：

• Batch gradient descent：Use all M examples in each iteration；
• Stochastic gradient descent：Use 1 example in each iteration；

然而这一节讲到的Mini-batch gradient descent是如下定义的：

• Mini-batch gradient descent ：Use b examples in each iteration；

  这里的mini-batch就是我们训练模型的时候的那个batch，上面的Batch gradient descent是全部的数据当作一次step或者iteration

---

那么用伪代码的形式表示就是：

一般来说\(b \in[2,100]\)，这里吴恩达常用b=10；

---

• 相比于Batch gradient descent，Mini-batch gradient descent的收敛速度更快；
• 相比于Stochastic gradient descent ，Mini-batch gradient descent只有在有一个good vectorized implementation的时候收敛速度会好与随机梯度下降
• 一个good vectorized implementation是可以实现数据的并行运算，这样同一时间内的运算个数肯定是大于1的，那么在速度上也就优于Stochastic gradient descent

20.3 Stochastic gradient descent converge

这一节主要是来讨论如何判断Stochastic gradient descent已经收敛到合适的位置了，同样重要的一件事——如何确定学习率\(\alpha\)。

---

其实如何判断是否收敛的方法就是——画梯度图像。

回顾之前的Batch gradient descent方法，定义\(J_{train}(\theta)=\frac{1}{m} \sum \limits_{i=1}^m(h_{\theta}(x^{(i)})-y^{(i)})^2\)为损失函数，然后通过画出迭代的损失函数数值图像，便可以看出函数是否是处于收敛状态。

而Stochastic gradient descent方法是，定义了\(cost(\theta,(x^i,y^i))=\frac{1}{2}(h_{\theta}(x^{(i)})-y^{(i)})^2\),在学习过程中，在更新\(\theta\)之前，只需要计算\(cost(\theta,(x^i,y^i))\)就好。

可以发现相比于Batch gradient descent，Stochastic gradient descent算法可以不用将全部的数据进行计算，便能够实现参数的更新，那么在绘制图像也就更快一些。

通常情况下，不是每经过一次迭代就画一次图像，而是1000次迭代(也就是处理完1000个examples)之后，求出1000个example的平均值，再去画一次图像上的点。有了这些点的数据集，那么可以根据图像就知道是否收敛，是否出现问题等情况。

---

那么接下来看几组图像(Plot \(cost(\theta,(x^i,y^i))\))。

• 第一组

由于是经过1000个样本进行一步图像绘制，因此可能不是每一步都是处于下降的过程中，也就是说存在噪声(对应于蓝色曲线)：

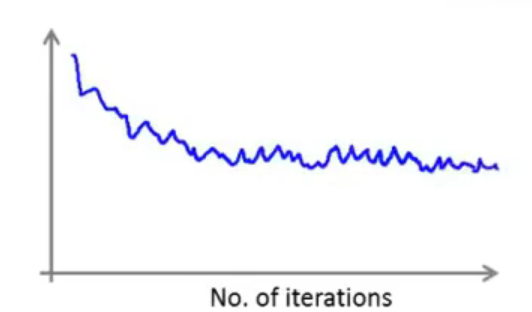
虽然可以从大体上看出，函数是处于收敛的状态的，那么如果进行修改参数，比如尝试使用一个更小的学习率(对应红色曲线)

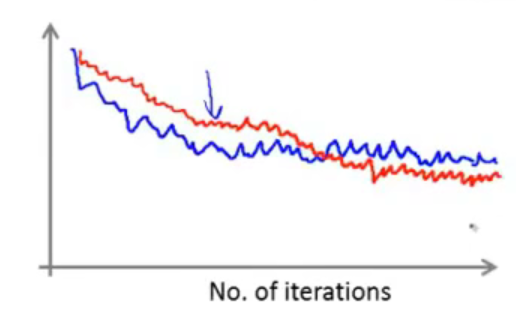
因为学习率\(\alpha\)​减小，那么收敛的速度也就相对来说变慢了，从图像上来说图像是下降变缓了，可能会相比于没有修改学习率会得到一个更好的结果。

出现上述情况的原因是随机梯度下降算法不是直接收敛到全局最小值的，而是在一个合理的范围内震荡，最终收敛到全局最小值处。 通过减小\(\alpha\)，此时的震荡幅度就没有那么的大了。

• 第二组

假设还是以1000个样本为单位，那么假设得到的图像如下图中蓝色的曲线效果，此时，如果改成5000个样本为单位，那得到的效果如下图中红色的曲线效果：

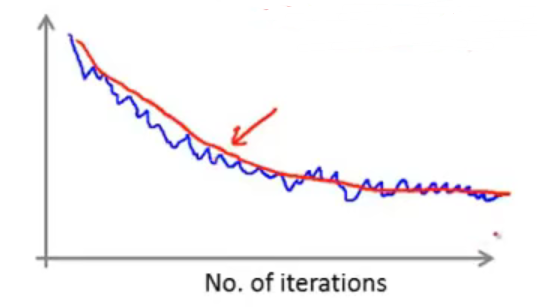
虽然得到的曲线更加平滑，但是更新的速度慢了很多。

• 第三组

假设你得到的图像是如下图所示：、

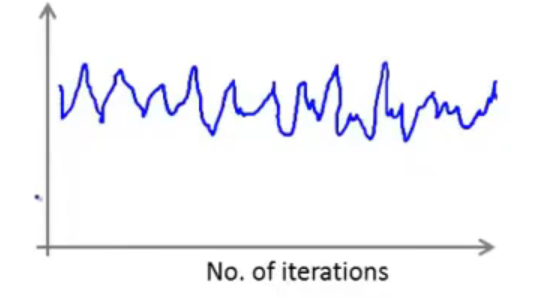
大体上来看，震荡幅度很大，而且也看不出是收敛还是发散的状态，这时，如果增加数量，也就是在“第二组”中讨论的情况，那么得到的效果图如下图红色曲线：

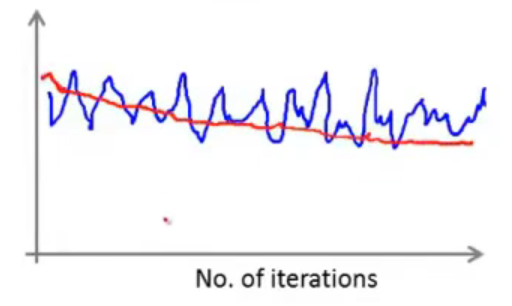
可以看到，算法本身还是处于收敛状态的，只是用于求均值的样本定义的过小了。

但是如果将用于求均值的样本数量定义的很大了，但是图像依然呈现出水平线的情况，如下图洋红色的曲线所示:

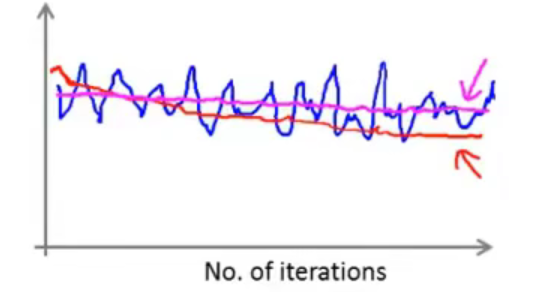
此时就说明，算法没有进行学习，算法本身出现了问题，需要仔细查找问题。

• 第四组

如果是呈现出发散的趋势：

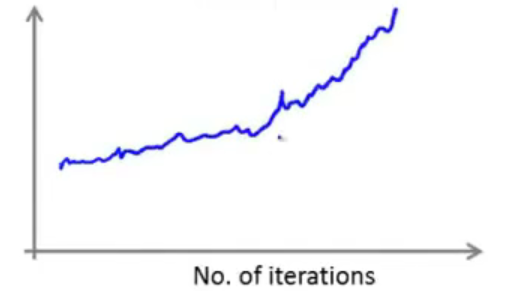
那么就需要将学习率变小。

总结一下：根据上述不同的曲线变化情况，需要做到对症下药。

---

最后再说一说学习率\(\alpha\)的取值问题，一般来说学习率是在迭代过程中是一个常量，不会发生改变，那么在图像上看就是函数是在一个范围内不断地震荡直到收敛：

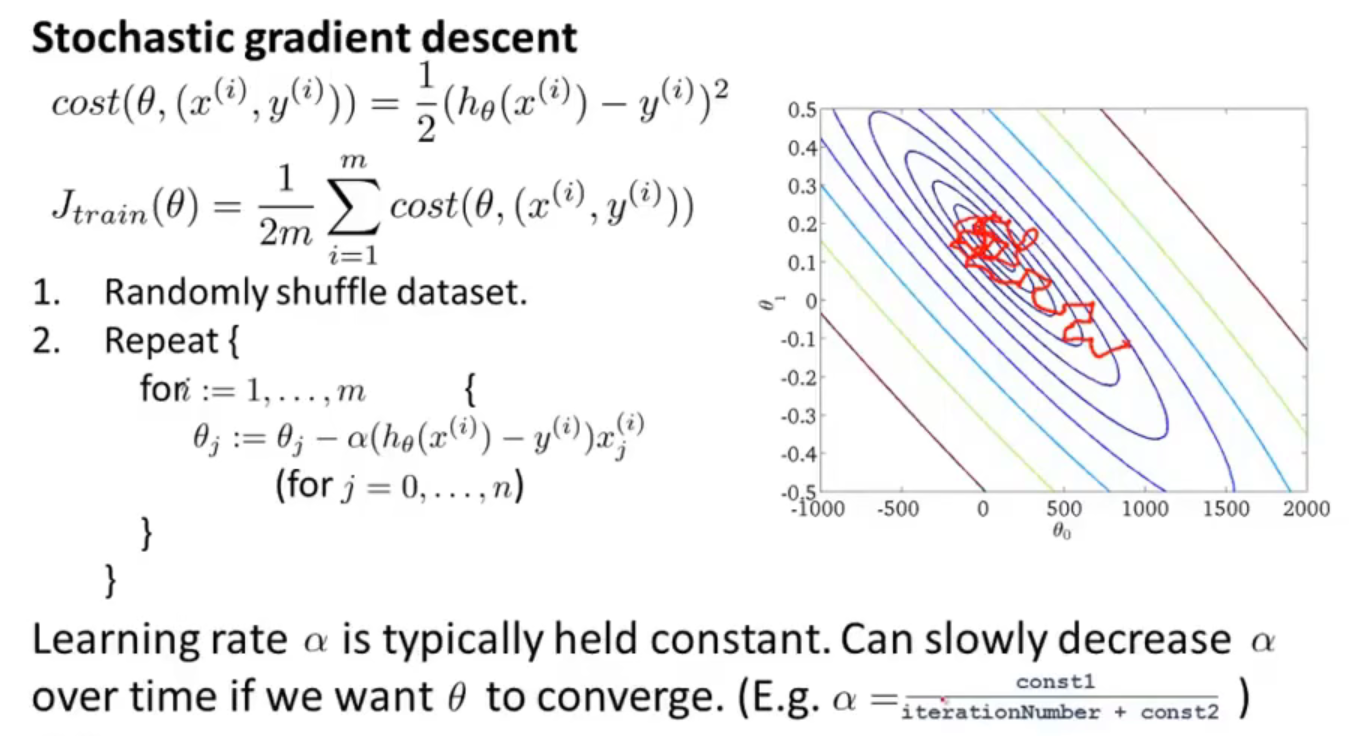
但是如果想要更好地收敛，那么就可以不断地去减小\(\alpha\)这样，最好是\(\alpha=0\)最后到达收敛的状态。

但是这样的处理需要自己确定两个参数const1和const2，并且还需要在迭代过程中维护这两个数值。

总结来说，定义\(\alpha\)​是一个常量就足以满足我们的要求了。

---

总结：这一小节提出了一种方法，不用将全部的example遍历一遍再去看是否收敛，只需要看每1000组数据的效果便足以近似代替真正的收敛效果，同时这种方法也是可以用于调整学习率\(\alpha\)

---

20.4 Online learning

这一节主要是来讨论一种新的大规模的机器学习机制(算是随机梯度下降算法的变种)——Online learning setting。

这种方法的一个应用就是在许多的大型网站中或者许多大型网络公司中，通过分析用户的数据流，学习用户的兴趣偏好，从而达到优化网站的决策。

---

Example 1

假设你有一个运输公司，公司提供了若干个运输业务套餐让客户来进行选择，同时需要客户来提供要价、起点和目的地等信息，对于这些信息统一用x表示，即Feature x capture properties of user，of origin/destination and asking price and etc.

我们期望的是希望可以构建一个用户选择较多的套餐模型，进而来调整价格，即learn \(p(y=1|x;\theta)\)，其中y=1表示用户选择，y=0表示用户没有选择。

通过构建出这样的一个模型，那么就可以很好地针对用户来提供一个好的解决方案。

---

Example 2

第二个例子是一个搜索平台的应用例子，比如平台有100部手机在售，用户在该平台上搜索手机关键字，推送满足条件的10部手机，那么这10部该如何选择给用户，才能使用户点击打开的概率最高。

同Example1中提到的一样，定义构建Feature x of phone，主要是包括手机的各种属性信息。

我们需要做的是预测用户点击的概率，用y=1表示用户点击，用y=0表示用户没有点击推送的链接。根据用户搜索的关键字来与手机的x进行最大匹配，从而达到预测概率的目的。

这类学习问题被称作predict click-through rate(CTR问题)。

在学习的过程中，通过用户搜索，推送给用户10个链接，同时也是10个标签(x,y)，根据用户的点击与否，可以确定y的取值是0还是1，这个过程就达到了一个训练的过程，对于获得的10个样本进行梯度下降法来更新参数，然后丢弃，重新再选择10个最新的数据，做同样的处理。

---

总结：虽然说像这样的网址也是可以构建一个固定的数据集来反反复复的训练模型，但是对于大公司，在那么多数据的前提下，重复使用数据也不利于保存，因此就是用Online-learning来实现在线训练的效果。

这种方法也有一个优点就是，如果有一个缓慢变化的用户群体，那么该算法也可以不断地调试模型参数，从而达到最新的用户行为的推荐。

20.5 MapReduce and data parallelism

整个篇幅将的算法都是可以运行在单台机器上的，但是若是数据非常大，难以通过一台机器来实现计算该怎么办呢，这一节就是来解决这个问题的。

虽然整个20节的前4个小节都是在讲Stochastic gradient descent，但是MapReduce同样与随机梯度下降算法一样重要。

---

简单来说MapReduce就是通过实现并行计算，从而达到加快计算速度的目的。

假设数据集有400个examples(400只是用来举例子的，400的数据集算是小的),同时存在着4台设备，那么首先是将数据集尽量分成4等份，那么每一台主机分别计算100组数据，最后的数据在中央计算机上进行整合就完成了并行计算的目的。

以Batch gradient descent为例，在进行梯度下降的时候，每台设备计算100个例子：

用逻辑图来表示就是：

---

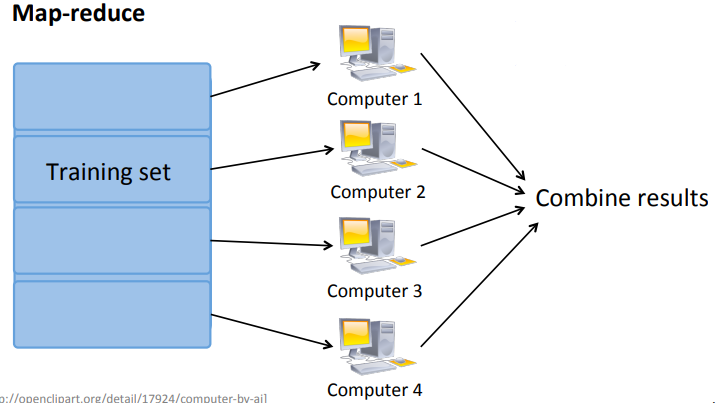
在不同的主机上进行并行计算的时候，需要考虑网络的速度问题，因此又存在另外一种实现方法——在本地进行计算。

我们知道不管是我们的CPU还是GPU都是多个核(core)的，因此我们可以在core上进行并行计算，也就是如下图所示：

---

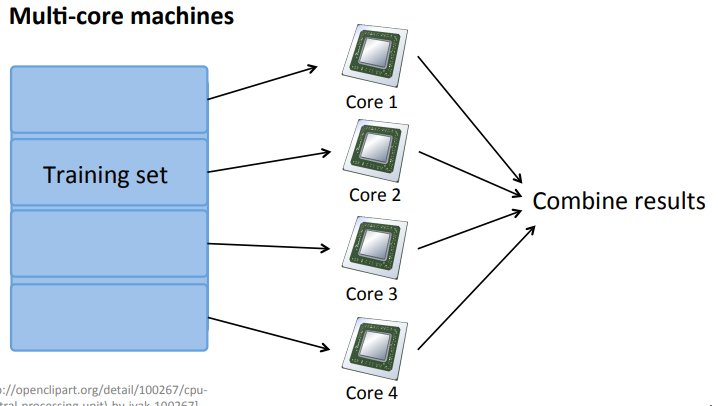
总结：

直到最后，吴恩达说到，开源的MapReduce的系统——Hadoop，我才发现，这一节讲到的知识就是Hadoop的里面的MapReduce。(taicaile).

21. Application example: Photo OCR

The reason why introduce Photo OCR

• An example of how a complex machine learning system can be put together;
• A concept of machine learning pipeline and how to allocate resources when you decide what to do next;
• Through the OCR , you can learn more interesting ideas for machine learning

21.1 Problem description and pipeline

Photo OCR stand for Photo Optical Character Recognition。

---

OCR问题是为了让计算机可以读取到图片中的文字信息。

整个流程包括文字检测，字符分割，字符分类：

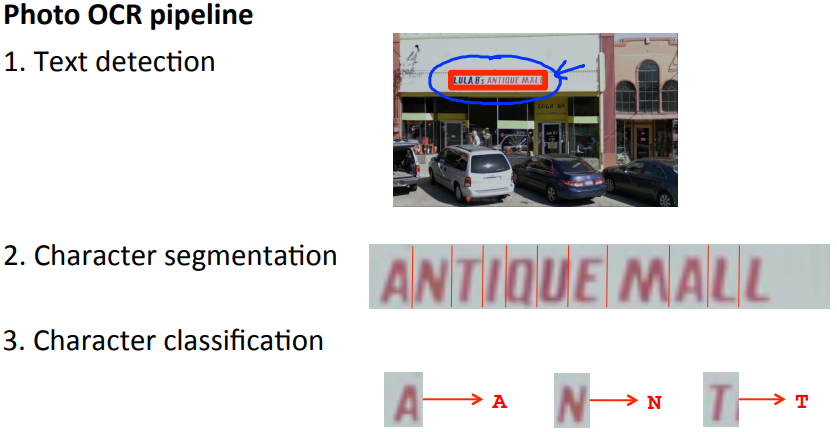
用流水线的逻辑图表示如下：

通常来说，既然是流水线，那么后面三个模块是需要用到三个小组的人员来参与开发的过程。

上述便是一个OCR系统的开发流程。

21.2 Sliding windows

这一节主要讲一个叫做sliding windows classifier的东西。

---

前面讲到了，什么是OCR和OCR的流水线设计，那么对于OCR 来说，第一步就是Text detection。

Text detection 在计算机视觉中是一个比较复杂困难的问题，因为需要在图片中找到文字的位置，期间还需要用大小不同的矩形将其全部框出，才可以完成Text detection 的工作。

---

为了简化讲述过程，先用行人检测的方法来进一步引申OCR问题。

从上图中可以看出，相比于OCR问题，Pedestrian detection的矩形框大小都是差不多大小，那么也即是可以用一个固定大小比例的矩形来表示了。

依据滑动窗口的性质，首先是要确定窗口的大小，然后利用监督学习的方法来选择正负样本集，假设滑动窗口的大小事82*36，效果如下图所示：

通过定义窗口每次滑动的步长，来在整个图片上获取图片，之后再通过classifier进行分类：

最终将会检测到图片中所有的行人：

---

Text detection

那么回到文字检测中，与Pedestrian detection一样，Text detection 也是需要用正负样本来确定当前窗口是否是包含了文字，我们定义有文字的为正样本，没有文字的表示为负样本(现在的正样本看起来不包含单个文字信息，因为现阶段只是用于检测是否包含文字，而不是确定包含的文字是什么，故classifier只需要知道这个地方有无文字即可)：

通过滑动窗口和二值化处理，然后便得出了下图的效果：

可以看出效果，白色的区域表示分类器认为有文字出现，黑色区域表示分类器认为没有文字出现。

我们下一步就是要实现文字区域的框出，但是文字识别的矩形大小是不一样的，也就是说不像Pedestrian detection那样的矩阵呈现出比例，因此需要用到expansion operator。

expansion operator的作用简单来说就是将在一定范围内的白色块连接成一个区域，这样就可以把一整个文字区域标出了(下图中右边的表示处理之后的图像)：

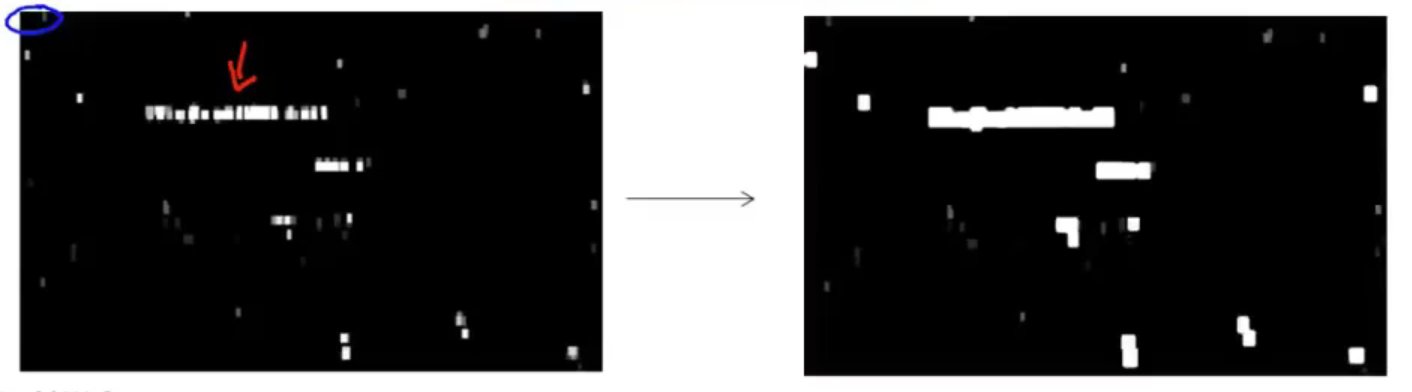
至于保存什么样子的白色区域，吴恩达给出的思路是保留横着的矩形区域，丢弃竖着的矩形区域，也就是根据长宽比来确定是横着还是竖着，最终标出三个区域如下图红框所示。

---

Character segmentation

OCR的第二步就是文字分割，这一步还是利用了supervise learning的方法，将文字的分界线图片表示正样本，其他的情况表示负样本：

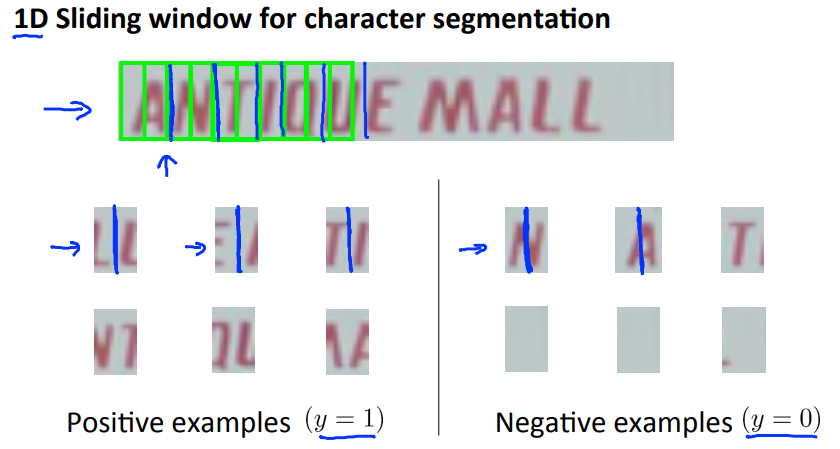
这样的话，通过滑动窗口，可以分割出单个字母的位置了。

---

Character classification

这部分就是前面讲到的模型训练，训练字母识别的即可，在此不再赘述。

综上便是整个OCR的大体流程了。

21.3 Getting lots of data: Artificial data synthesis

得到高性能机器学习系统，最可靠的方法就是使用一个low bias learning algorithm with a massive training set。

在机器学习领域有一个很棒的概念就是——Artificial data synthesis，但是这个方法并不适合所有的问题，只是适用于一些特定的问题。

人工数据合成主要有两种形式：

• 第一种是从头开始创建新的数据；
• 第二种是通过已有的小的标签训练集，通过扩充方法，变成一个大的训练集

下面将依次讲述这两种方法。

---

• 第一种形式

还是以OCR为例，假设现在已经存在了一个数据集：

但是如果想要获得一个新的，更大的数据集，该怎么处理呢？

若是从零开始创建一个数据集，那么对于OCR来说，是有一个字体库可以使用的，通过这个字体库可以将所有的字母不断地进行转换，这样就构成了一个数据集。

通过利用字体库的方法，实现了一个合成的数据集：

对于获得的数据集还可以用模糊处理(blurring operator)，或者仿射变换(affine distortions)等方法再去处理一下数据。

• 第二种形式

对于第二种方法，是通过现有的数据，来将原有的数据进行扩充，比如现在有一个数据图像，通过artificial warpings或者说artificial distortion：

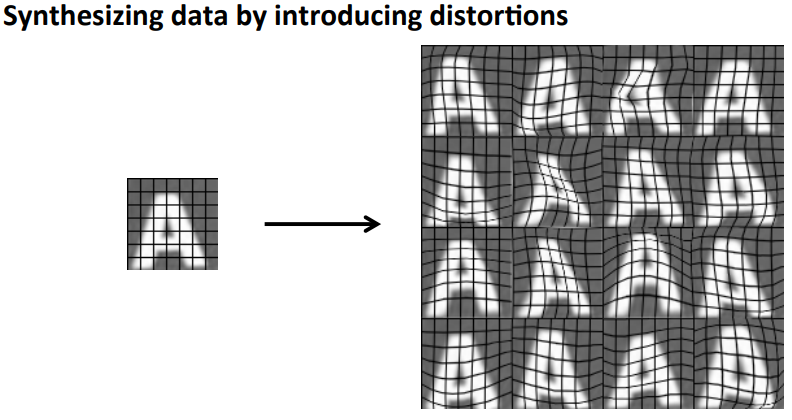
对于第二种方法，你要能够清楚地知道哪些操作是可以对算法有提高效果的，如果没有效果那么就是白做工了。

再举一个语音方面的例子：

通过在源数据上添加一些噪点，从而达到扩充数据集的目的。

总得来说，你扩充的数据应该要有代表性，不能盲目对源数据进行失真(distortion)处理，

不如你对字母“A”增加了亮度，那么对数据集来说就是没有任何效果的；

因此需要认真考虑添加哪些失真才能对算法是有意义的；

---

对于获取更多数据这个层面来说，需要注意：

21.4 Ceiling analysis：What part of the work is the best use of your time to work on

对于机器学习来说，或者研究人员来说，最重要的就是要注意时间，最需要的也是时间，因此这一节主要讨论的是Ceiling analysis 可以通常给出一个有价值的信息去指导下一步的工作中哪一部分是最值得花时间研究的。

---

还是以OCR为例来讲解什么是Ceiling analysis。

我们知道，OCR是分为了4个步骤来实现的，那么这4个步骤中哪一个步骤才是最重要的呢，那么这就是上限分析(ceiling analysis)要做的事情。

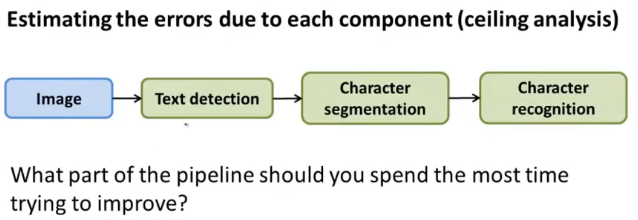
假设当前的算法在test set 上的准确度是72%：

下面就是ceiling analysis的设计思路了，现在我们针对Text detection模块进行处理，现在把整个test set的正确性告诉Test detection，换句话说就是告诉Text detection模块，当前测试数据中包含的正确字符是什么，这样就可以使Test detection的模块准确性达到100%，然后再测得整个检测系统的accuracy从原来的72%提升到现在的89%：

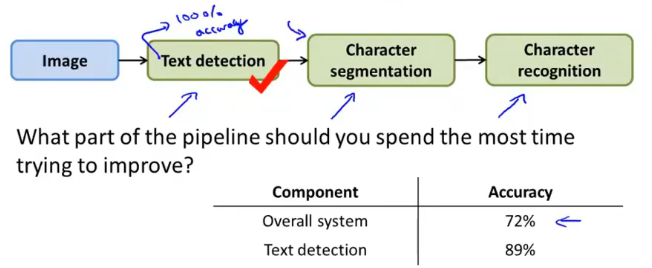
同样的处理方法，在Text detection模块的准确率达到100%的前提下，再对Character segmentation做同样的处理，把整个test set的正确性告诉Character segmentation，然后让Character segmentation模块的正确性达到100%，最后测到整个系统的检测准确率从原来的89%上升到现在的90%：

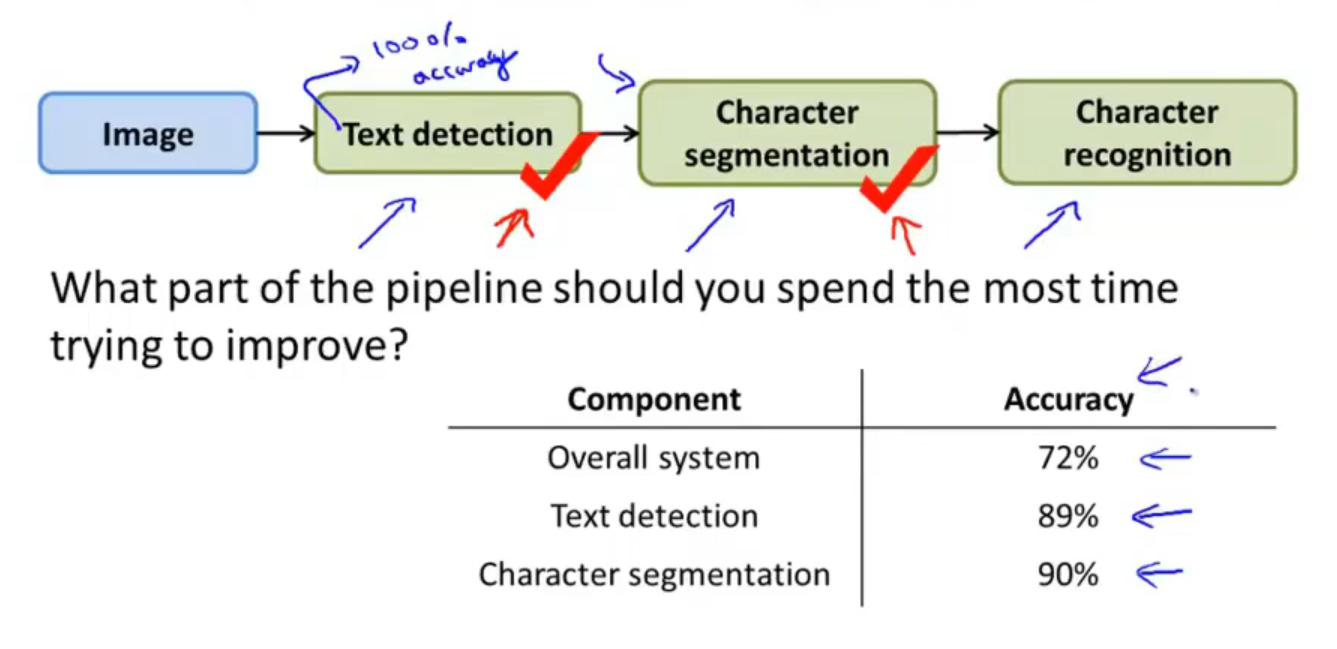
同理再对Character recognition做同样地处理，最后整个系统的accuracy达到100%：

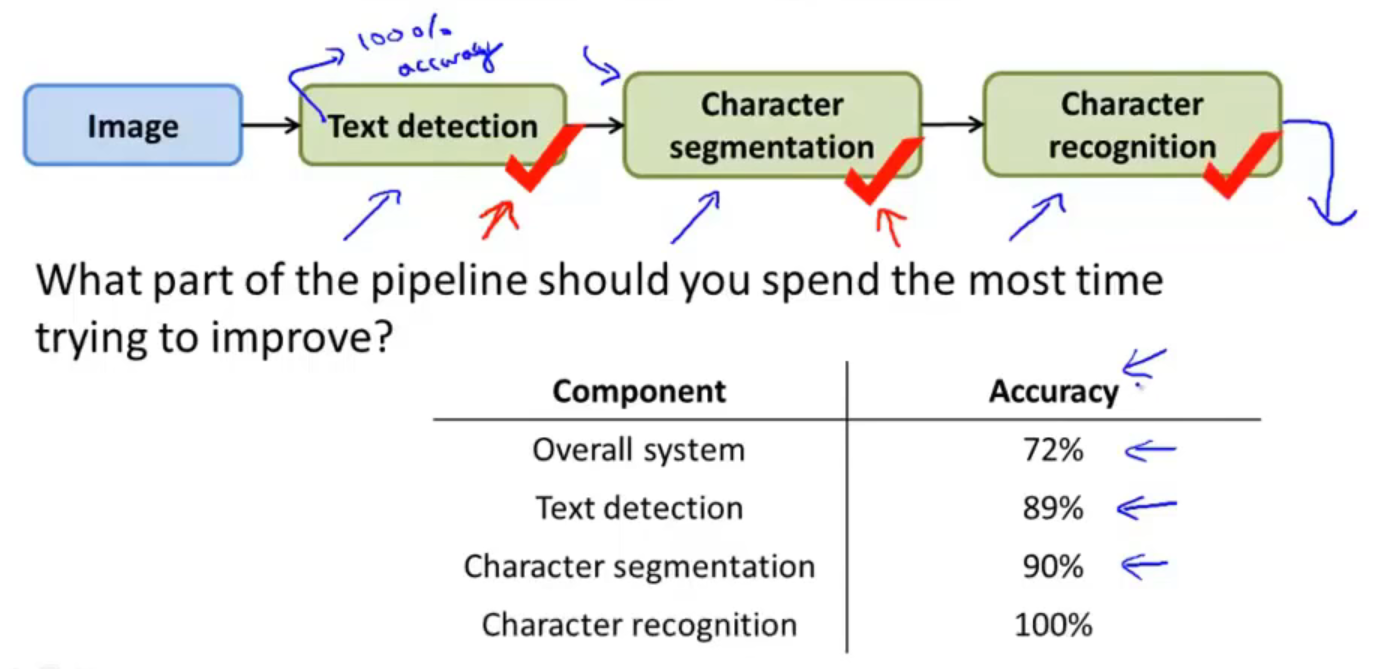
至此，会有一个问题：这样做的目的是什么呢？

答：首先需要明确的是，我们告诉每一个模块的整个测试集的正确性，是为了得到该模块在整个系统中达到极致的时候准确率是什么样子的，因此可以看出：

• Text detection 达到极致的时候，可以将整个测试系统的准确率提升17%(89%-72%)；
• Character segmentation达到极致的时候，可以将整个测试系统的准确率提升1%(90%-89%);
• Character recognition达到极致的时候，可以将整个测试系统的准确率提升10%(100%-90%)；

因此可以看出想要提高整个系统的算法效果，应该重点去在Text detection和Character recognition这两个模块上进行修改，而不是性价比低的Character segmentation部分。

这就是ceiling analysis的思想。

---

再举一个稍微复杂的例子—— face recognition

假设设计一个如下图所示的模型，主要有Preprocess(去掉整张图片的背景图)、Face detection(面部检测，应用滑动窗口的实现)，eyes segmentation、nose segmentation、mouth segmentation 和 logistic regession这几个部分。

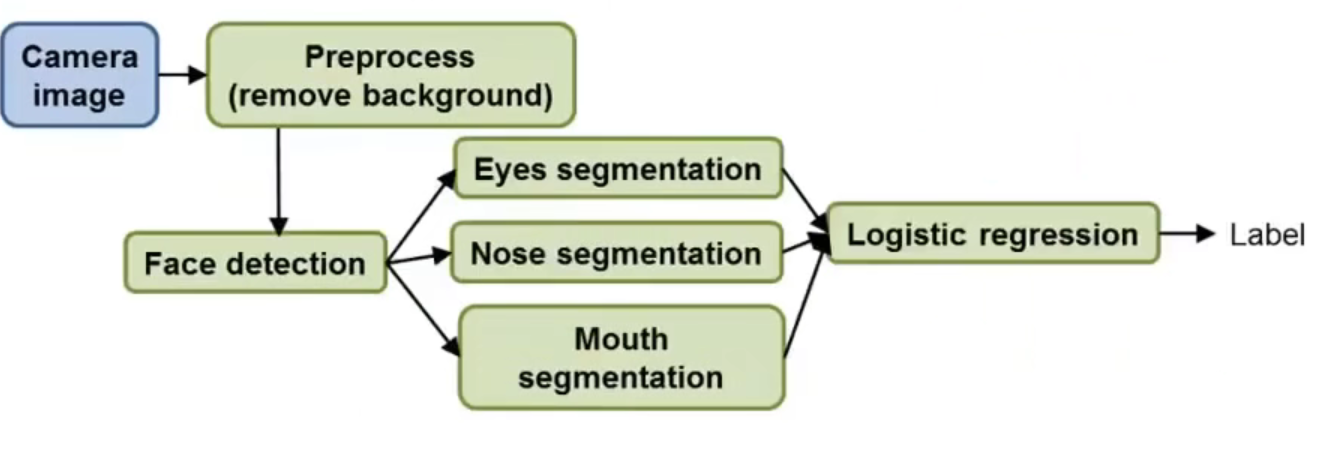
那么根据在OCR部分讲到的ceiling analysis的设计思路，在Face recognition部分就是要对上面讲到的6个模块分别处理，可以得出如下图所示的结果：

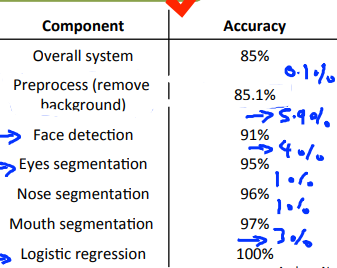
那么根据结果可知，针对Face detection和eyes segmentation模块的修改可以很好的提高整个系统的准确性。

插一句题外话，吴大佬说真的有一个research team在Preprocess这个模块上花费了18个月的改进，最后的结果可想而知是很不理想的，因为对整个系统的提升效果才不到1%

---

总结来说，对于一个研究者来说，时间是非常宝贵的，所以千万不要将时间花费在到头来没有意义的一件事情上。

22. Summary: Main topics

• Supervised Learning

  • Linear regression；
  • logistic regression；
  • neural networks；
  • SVM；

• Unsupervised Learning

  • K-means；
  • PCA；
  • Anomaly detection；

• Special applications

  • recommender system；
  • large scale machine learning；

• Advice on building a machine learning system

  • Bias/variance；
  • regularization；
  • deciding what to work on next；
  • evaluation of learning algorithm；
  • learning curves；
  • error analysis；
  • ceiling analysis；