机器学习笔记1
1. 介绍
1.1 什么是Mechine Learning
Definition:A computer program is said to learining from experience E with respect to some task Tand some performance measure p, if its performance on T, as measured by P, improveswith experience E.
翻译来说:计算机程序从经验E中学习,解决某一任务T,获得衡量标准P;
简单来说可以认为:
- E表示经验值;
- T就是需要做的任务;
- P是正概率;
1.2 类型
目前有很多种不同类型的学习算法,其中最主要(常用)的两类是supervised learning(监督学习)& unsupervised learning(无监督学习)
Other:Reinforcement learning(强化学习) , recommeder systems, etc.
对于supervised learning简单解释来说,就是我们教计算机去做某些事情;在unsupervised leaning 中是让计算机自己去学习。
2. Supervised Learning(监督学习)
2.1 Definition
给定一个正确的样本集进行训练,目的就是为了推测出更多正确的答案。
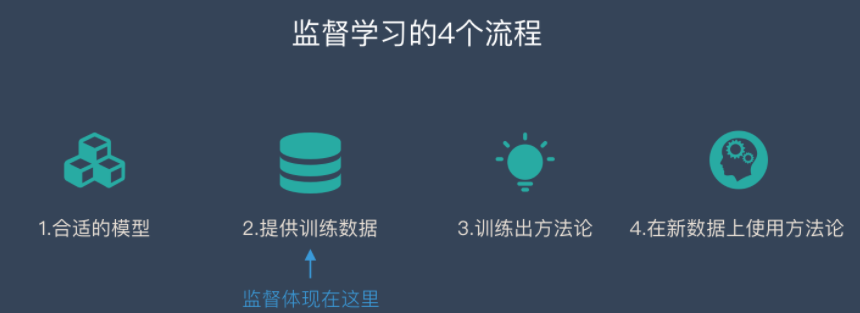
Supervised learning 有两个任务,分别是Regression problem(回归问题)和Classification problems(分类问题)

2.2 Regression Problem
回归问题是用来预测连续的和具体的数值。
比如房价的预测,支付宝里面的芝麻信用分数,这些都是回归问题。
下面要说的是个人信用评估方法——FICO。
他跟芝麻信用类似,用来评估个人的信用状况。FICO 评分系统得出的信用分数范围在300~850分之间,分数越高,说明信用风险越小。
下面我们来模拟一下 FICO 的发明过程,这个过程就是监督学习力的回归。
步骤1:构建问题,选择模型
我们首先找出个人信用的影响因素,从逻辑上讲一个人的体重跟他的信用应该没有关系,比如我们身边很讲信用的人,有胖子也有瘦子。
而财富总额貌似跟信用有关,因为马云不讲信用的损失是非常巨大的,所以大家从来没有听说马云会不还信用卡!而一个乞丐不讲信用的损失是很小的,这条街混不下去了换一条街继续。
所以根据判断,找出了下面5个影响因素:
- 付款记录
- 账户总金额
- 信用记录跨度(自开户以来的信用记录、特定类型账户开户以来的信用记录…)
- 新账户(近期开户数目、特定类型账户的开户比例…)
- 信用类别(各种账户的数目)
这个时候,我们就构建了一个简单的模型:

f 可以简单理解为一个特定的公式,这个公式可以将5个因素跟个人信用分形成关联。
我们的目标就是得到 f 这个公式具体是什么,这样我们只要有了一个人的这5种数据,就可以得到一个人的信用分数了。
步骤2:收集已知数据
为了找出这个公式 f,我们需要先收集大量的已知数据,这些数据必须包含一个人的5种数据和他/她的信用状态(把信用状态转化为分数)。
我们把数据分成几个部分,一部分用来训练,一部分用来测试和验证。

步骤3:训练出理想模型
有了这些数据,我们通过机器学习,就能”猜测”出这5种数据和信用分数的关系。这个关系就是公式 f。
然后我们再用验证数据和测试数据来验证一下这个公式是否 OK。
测试验证的具体方法是:
- 将5种数据套入公式,计算出信用分
- 用计算出来的信用分跟这个人实际的信用分(预先准备好的)进行比较
- 评估公式的准确度,如果问题很大再进行调整优化
步骤4:对新用户进行预测
当我们想知道一个新用户的信用状况时,只需要收集到他的这5种数据,套进公式 f 计算一遍就知道结果了!
好了,上面就是一个跟大家息息相关的回归模型,大致思路就是上面所讲的思路,整个过程做了一些简化,如果想查看完整的过程,可以查看《机器学习-机器学习实操的7个步骤》
2.3 Classification Problem
分类问题是用于解决预测离散的问题。
比如吴恩达提到的乳腺癌的预测,肿瘤良性与否。
下面以是否离婚与否来解释。
美国心理学家戈特曼博士用大数据还原婚姻关系的真相,他的方法就是分类的思路。
戈特曼博士在观察和聆听一对夫妻5分钟的谈话后,便能预测他们是否会离婚,且预测准确率高达94%!他的这项研究还出了一本书《幸福的婚姻》(豆瓣8.4分)。
步骤1:构建问题,选择模型
戈特曼提出,对话能反映出夫妻之间潜在的问题,他们在对话中的争吵、欢笑、调侃和情感表露创造了某种情感关联。通过这些对话中的情绪关联可以将夫妻分为不同的类型,代表不同的离婚概率。
步骤2:收集已知数据
研究人员邀请了700对夫妻参与实验。他们单独在一间屋子里相对坐下,然后谈论一个有争论的话题,比如金钱和性,或是与姻亲的关系。默里和戈特曼让每一对夫妻持续谈论这个话题15分钟,并拍摄下这个过程。观察者看完这些视频之后,就根据丈夫和妻子之间的谈话给他们打分。

步骤3:训练出理想模型
戈特曼的方法并不是用机器学习来得到结果,不过原理都是类似的。他得到的结论如下:
首先,他们将夫妻双方的分数标绘在一个图表上,两条线的交叉点就可以说明婚姻能否长久稳定。如果丈夫或妻子持续得负分,两人很可能会走向离婚。重点在于定量谈话中正负作用的比率。理想中的比率是5∶1,如果低于这个比例,婚姻就遇到问题了。最后,将结果放在一个数学模型上,这个模型用差分方程式凸显出成功婚姻的潜在特点。
戈特曼根据得分,将这些夫妻分成5组:
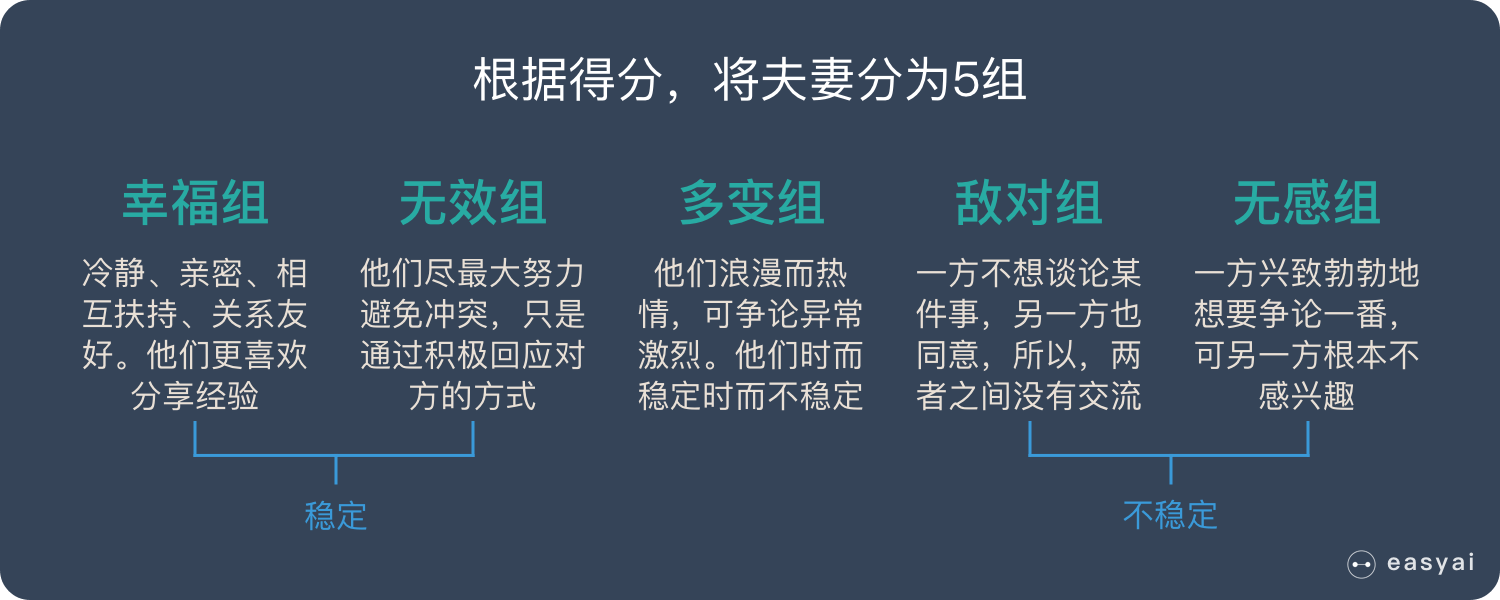
- 幸福的夫妻:冷静、亲密、相互扶持、关系友好。他们更喜欢分享经验。
- 无效的夫妻:他们尽最大努力避免冲突,只是通过积极回应对方的方式。
- 多变的夫妻:他们浪漫而热情,可争论异常激烈。他们时而稳定时而不稳定,可总的来说不怎么幸福。
- 敌对的夫妻:一方不想谈论某件事,另一方也同意,所以,两者之间没有交流。
- 彼此无感的夫妻:一方兴致勃勃地想要争论一番,可另一方对讨论的话题根本不感兴趣。
该数学模型呈现了两种稳定型夫妻(关系和谐的夫妻和关系不和谐的夫妻)和两种不稳定型夫妻(敌对夫妻和无感夫妻)之间的区别。而据预测,不稳定的夫妻可能会一直保持婚姻关系,尽管他们的婚姻不稳定。
步骤4:对新用户进行预测
12年以来,每隔一两年,默里和戈特曼都会与参与研究的那700对夫妻交流。两个人的公式对离婚率的预测达到了94%的准确率。
2.4 主流的监督学习的方法
| 算法 | 类型 | 简介 |
|---|---|---|
| 朴素贝叶斯 | 分类 | 贝叶斯分类法是基于贝叶斯定定理的统计学分类方法。它通过预测一个给定的元组属于一个特定类的概率,来进行分类。朴素贝叶斯分类法假定一个属性值在给定类的影响独立于其他属性的 —— 类条件独立性。 |
| 决策树 | 分类 | 决策树是一种简单但广泛使用的分类器,它通过训练数据构建决策树,对未知的数据进行分类。 |
| SVM | 分类 | 支持向量机把分类问题转化为寻找分类平面的问题,并通过最大化分类边界点距离分类平面的距离来实现分类。 |
| 逻辑回归 | 分类 | 逻辑回归是用于处理因变量为分类变量的回归问题,常见的是二分类或二项分布问题,也可以处理多分类问题,它实际上是属于一种分类方法。 |
| 线性回归 | 回归 | 线性回归是处理回归任务最常用的算法之一。该算法的形式十分简单,它期望使用一个超平面拟合数据集(只有两个变量的时候就是一条直线)。 |
| 回归树 | 回归 | 回归树(决策树的一种)通过将数据集重复分割为不同的分支而实现分层学习,分割的标准是最大化每一次分离的信息增益。这种分支结构让回归树很自然地学习到非线性关系。 |
| K邻近 | 分类+回归 | 通过搜索K个最相似的实例(邻居)的整个训练集并总结那些K个实例的输出变量,对新数据点进行预测。 |
| Adaboosting | 分类+回归 | Adaboost目的就是从训练数据中学习一系列的弱分类器或基本分类器,然后将这些弱分类器组合成一个强分类器。 |
| 神经网络 | 分类+回归 | 它从信息处理角度对人脑神经元网络进行抽象, 建立某种简单模型,按不同的连接方式组成不同的网络。 |
注:逻辑回归(Logistic Regression)与线性回归(Linear Regression)都是一种广义线性模型)(generalized linear model)
3. Unsupervised Learning(无监督学习)
3.1 Definition
什么是Unsupervised Learning,需要与Supervised Learning进行对比。
我们知道Supervised Learning 是有标签,即用于训练的数据是有明确的目的与明确已知的labels,那么Supervised Learning的反面就是Unsupervised Learning了。

总结来说就是:
Unsupervised Learning是一种利用统计手段为本质的方法,可以在没有标签(或者说有相同的标签)的数据里面发现一种结构来进行表示出不同的cluster——聚类算法。
3.2 无监督学习的使用案例
案例1:发现异常
有很多违法行为都需要"洗钱",这些洗钱行为跟普通用户的行为是不一样的,到底哪里不一样?
如果通过人为去分析是一件成本很高很复杂的事情,我们可以通过这些行为的特征对用户进行分类,就更容易找到那些行为异常的用户,然后再深入分析他们的行为到底哪里不一样,是否属于违法洗钱的范畴。
通过无监督学习,我们可以快速把行为进行分类,虽然我们不知道这些分类意味着什么,但是通过这种分类,可以快速排出正常的用户,更有针对性的对异常行为进行深入分析。
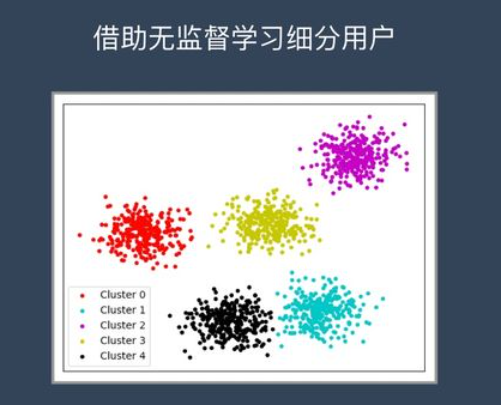
案例2:用户细分
这个对于广告平台很有意义,我们不仅把用户按照性别、年龄、地理位置等维度进行用户细分,还可以通过用户行为对用户进行分类。
通过很多维度的用户细分,广告投放可以更有针对性,效果也会更好。

案例3:推荐系统
大家都听过"啤酒+尿不湿"的故事,这个故事就是根据用户的购买行为来推荐相关的商品的一个例子。
比如大家在淘宝、天猫、京东上逛的时候,总会根据你的浏览行为推荐一些相关的商品,有些商品就是无监督学习通过聚类来推荐出来的。系统会发现一些购买行为相似的用户,推荐这类用户最"喜欢"的商品。
3.3 无监督学习常见的两种算法
聚类和降维
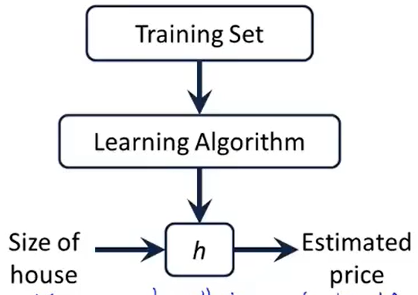
聚类:简单说就是一种自动分类的方法,在监督学习中,你很清楚每一个分类是什么,但是聚类则不是,你并不清楚聚类后的几个分类每个代表什么意思。
降维:降维看上去很像压缩。这是为了在尽可能保存相关的结构的同时降低数据的复杂度。
4. 模型描述
4.1 Univariate Linear regression
所谓的Univariate Linear regression就是Linear regression with one variable,即单变量的线性函数 \(h_\theta(x)=\theta_0+\theta_{1}x\) ,比如用这个函数来实现房价的预测等线性
回归的问题。

当然还有许多模型是非线性回归的问题,作为开始阶段只需要以简单的线性回归方程(一元线性回归方程)作为入门即可。
可以参考“线性回归方程的理解”一文
4.2 Cost function(代价函数)
4.2.1 Definition
代价函数这个概念可以让我们找到最适合我们数据的直线。(代价函数有点像损失函数的意思)
根据前一节可知,线性函数\(h_\theta(x)=\theta_0+\theta_{1}x\) 中的\(\theta_0\)和\(\theta_1\)是需要我们来确定的。
我们可以知道,根据不同的参数是可以得到不同的图像的,我们简单的举几个例子如下图所示:
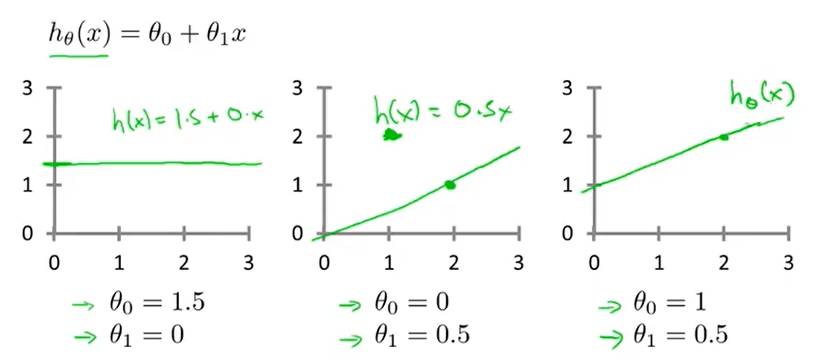
给定数据集,我们可以想到如果\(h_\theta(x)\)接近于y,那么就可以认为此时的\(\theta_0和\theta_1\)是最接近真实值的。
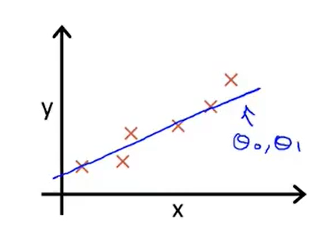
用公式来表达就是
也就是最小二乘法的应用。
上式就是所说的Cost Function,其中上式的\(\frac{1}{2M}\)是用来抵消求导之后的2的,主要是用来简化运算,不会对单调性产生影响。
为了便于进一步解释Cost Function,我们先简化\(h_\theta(x)=\theta_1(x)\) ,设\(J(\theta_1)=\frac{1}{2M}\sum\limits_{i=1}^M(h_\theta(x_i)-y_i)^2\)为Cost Function,那么最小化这个函数,也就是\(minimizeJ(\theta_1)\)。
那么通过不断地修改参数,可以得到\(J(\theta_1)\)与\(\theta_1\)之间的函数关系图,如下所示:
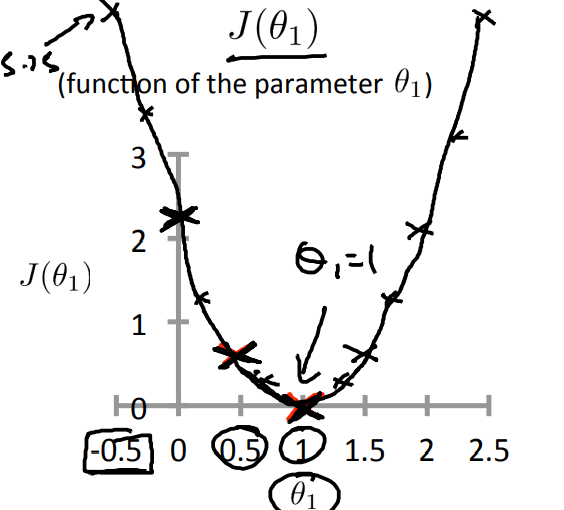
从图上可以看出,当\(\theta_1\)=1的时候是最小的时候,这与我们一开始预设的\(h_\theta(x),\theta_1=1\)很符合
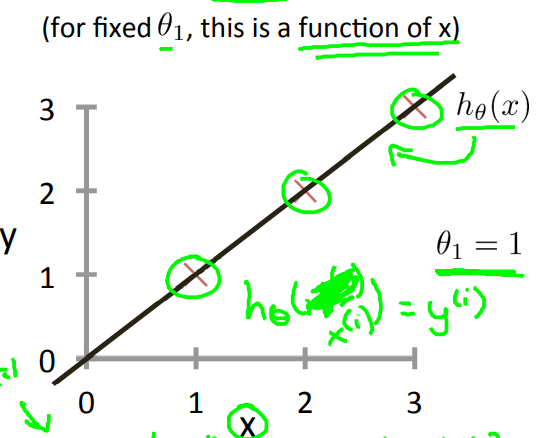
Square Error Function可以说是解决回归问题最常用的手段了。
这里为什么不能像求极大似然估计的方法一样来直接求导一次来计算最小值呢?为什么一定要用后面要用梯度下降的方法来一步步获得局部最优解的方法呢?
在博主的机器学习回归理论推导——以线性回归为例一文中详细的推导了回归理论,通过代价函数对参数求导,令其为零,得出参数为:
参数的结果给出两个信息,同时也是直接求导不可行的原因:
- X的转置乘以X必须要可逆,也就是X必须可逆,但是实际情况中并不一定都满足这个条件,因此直接求导不可行;
- 假设满足了条件一,那么就需要去求X的转置乘以X这个整体的逆,线性代数中给出了求逆矩阵的方法,是非常复杂的(对计算机来说就是十分消耗性能的),数据量小时,还可行,一旦数据量大,计算机求矩阵的逆将会是一项非常艰巨的任务,消耗的性能以及时间巨大,而在机器学习中,数据量少者上千,多者上亿;因此直接求导不可行。
相较而言,梯度下降算法同样能够实现最优化求解,通过多次迭代使得代价函数收敛,并且使用梯度下降的计算成本很低,所以基于以上两个原因,回归中多数采用梯度下降而不是求导等于零。
参考:https://blog.csdn.net/qq_41800366/article/details/86600893
4.2.1 What the cost function is doing
再进一步讨论有两个参数的情况,也就是当\(h_\theta(x) = \theta_1x+\theta_0\)的时候。那么此时这个函数的图像如下所示
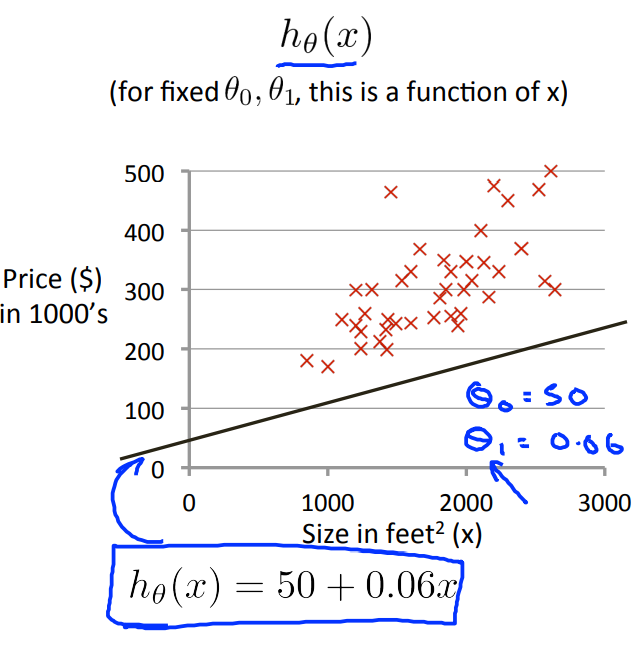
那么此时的Cost Function的图像应该类似于一个碗状的三维图像如下:
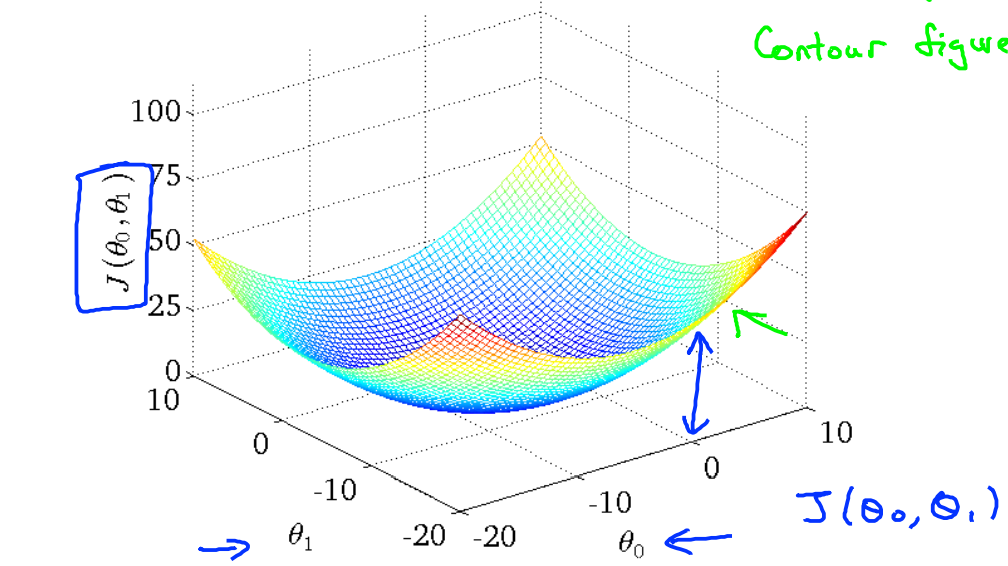
那么在这里使用Contour Figure(等高线图)来表示如下:
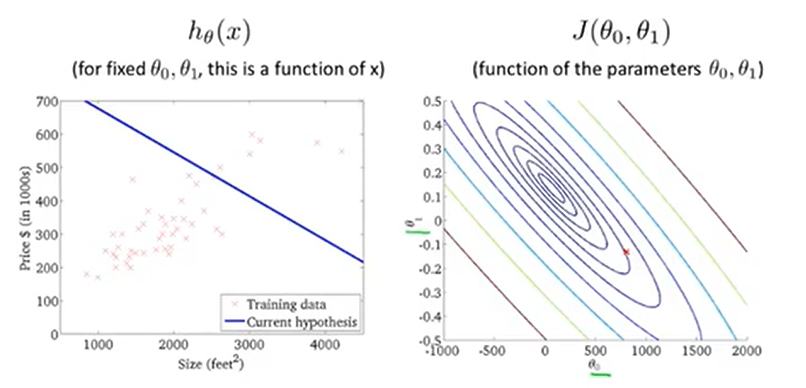
每一个椭圆线都表示\(J(\theta_0,\theta_1)\)相同的点。
下面随机去模拟几个数据,来说明contour figure的使用情况。
当取\(\theta_0=800,\theta_1=-0.15\)的时候,可以得出这个这个距离的平方和不是很小。
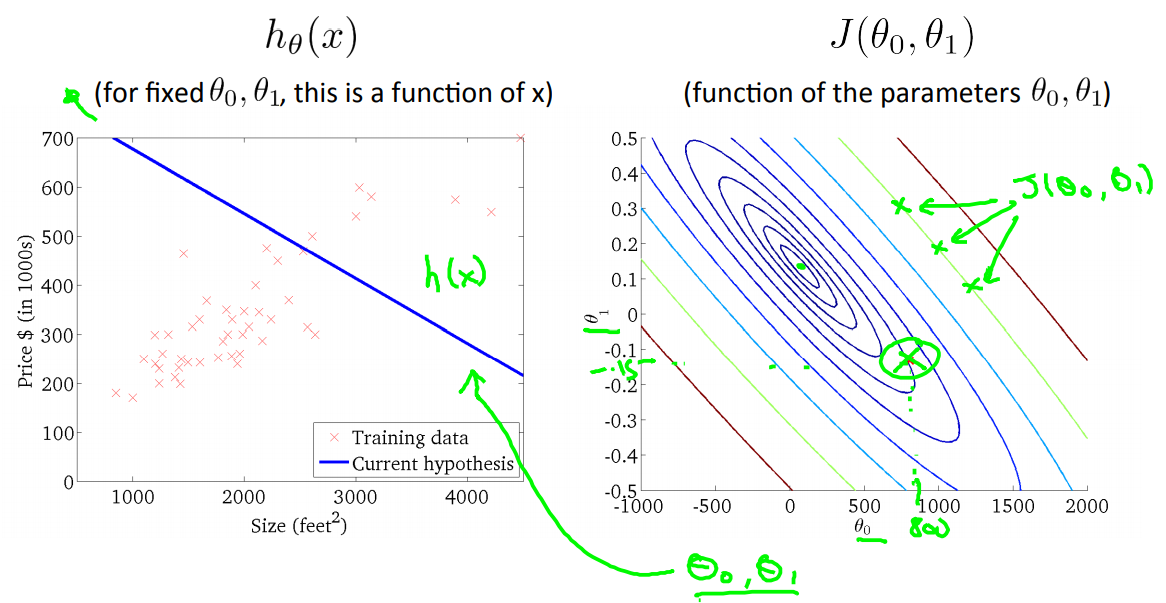
当取\(\theta_0=360,\theta_1=0\)的时候,发现cost function的值小了一些。
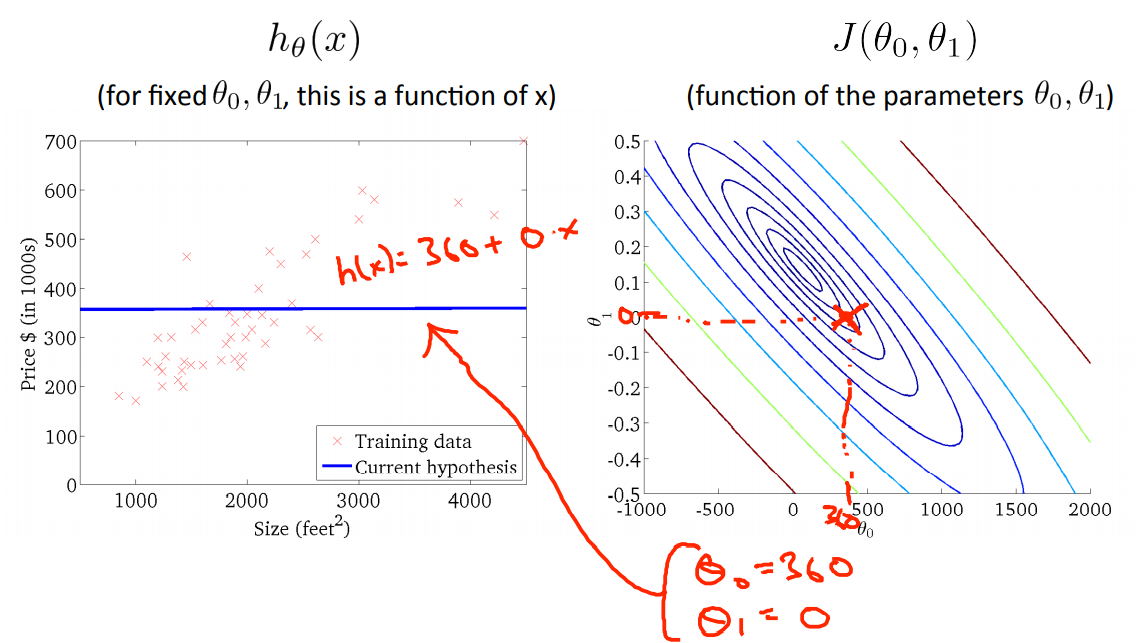
最后我们便模拟出一个最优的值作为最后的结果。
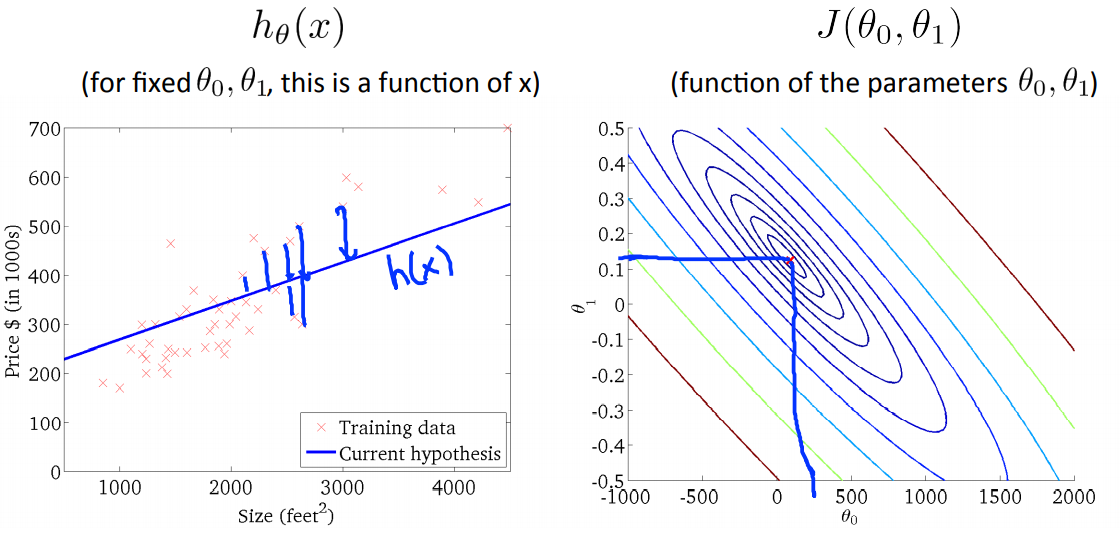
当然通过手动模拟多参数或者复杂的四维、五维的参数的时候是不现实的,因此需要利用其他的手段来计算出我们想要的结果。
5 Gradient Descent Algorithm(梯度下降法)
5.1 Introduce
Gradient Descent适用于求最小值,它不仅能够用于线性回归方程,也能够应用于其他的领域。
这里先以两个参数为例(实际的情况下,会存在很多个参数需要去调整)。
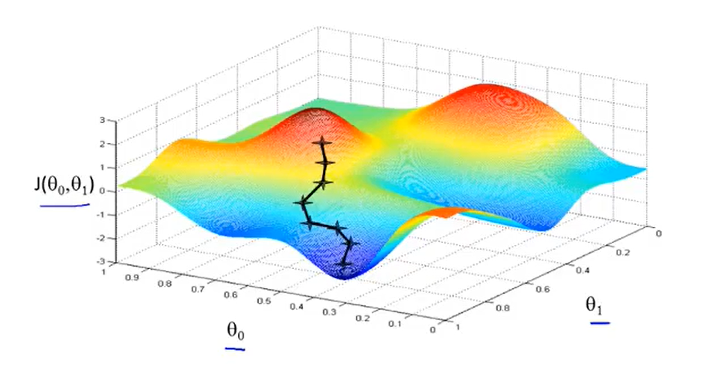
那么一开始先初始化两个参数值(初始化多少都可以,这里令\(\theta_0=\theta_1=0\),在三维的图像上可以看到其初始位置如下。
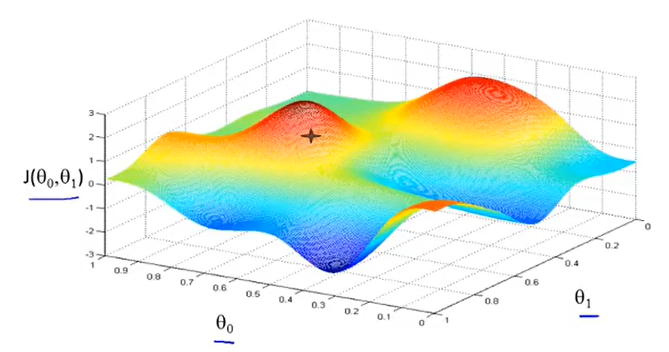
那根据gradient descent方法,需要找到一条”下山的路“才能够满足要求,那么得出的路线如下图所示。
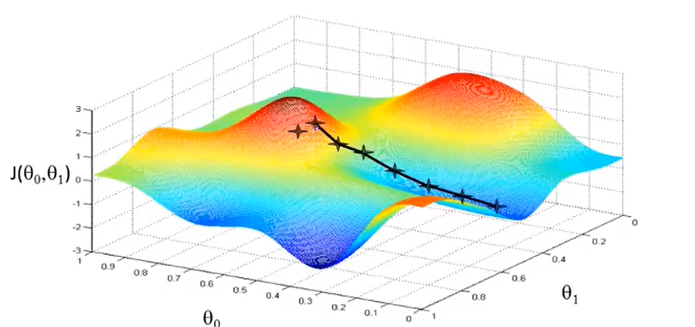
但是如果一开始偏移了一些,那么就可能找到另外一条”下山更快的路“,也就是再找到一个local optimum(局部最优解)如下图。
公式展示:

重复上述公式,使其达到收敛(convergence)的目的。
上述的公式中有一些细节需要注意:
- “:=”代表赋值的意思(assignment operator);
- “=”代表着真假判断(truth assertion);
- \(\alpha\)代表着在梯度下降的是时候,需要“迈多大的步子”,如果\(\alpha\)很大,那就代表着下降很快,反之就是下降得很慢,因此\(\alpha\)也被称作为learing rate;
- 梯度下降法应该是同步更新的,所谓的同步更新是指要更新的参数都应同步更新,下面就是非同步更新的意思:
-

- 虽然也可以实现正常的工作,但是不是我们所说的方法,其是具有不同性质的其他算法,非同步的方法可能会导致一些偏差值
在机器学习中,我们通常需要对问题进行建模,然后可以得到一个成本函数(cost function),通过对这个成本函数进行最小化,我们可以得到我们所需要的参数,从而得到具体的模型。这些优化问题中,只有少部分可以得到解析解(如最小二乘法),而大部分这类优化问题只能迭代求解,而迭代求解中两种最常用的方法即梯度下降法与牛顿法。
对于一个多元函数(假设是可微),其偏导数就表示在某一坐标轴方向的导数,比如\(z=x^2+y^3 ,\frac{\partial z}{\partial x^2}=2x\)就是沿着X轴方向上的导数,那么\(\frac{\partial z}{\partial y^3}=3y^2\)就是沿着Y轴方向的导数;
除开沿坐标轴方向上的导数,多元函数在非坐标轴方向上也可以求导数,这种导数称为方向导数。
很容易发现,多元函数在特定点的方向导数有无穷多个,表示函数值在各个方向上的增长速度。一个很自然的问题是:在这些方向导数中,是否存在一个最大的方向导数,如果有,其值是否唯一?为了回答这个问题,便需要引入梯度的概念。
梯度,本质上是一个函数全部偏导数构成的向量,表示方式如下图所示:

因为梯度的定义是:函数在某一点的梯度是这样一个向量,它的方向与取得最大方向导数的方向一致,而它的模为方向导数的最大值。
也就是说沿着梯度的方向,那么就是方向导数最大的方向。
当我们讨论函数沿任意方向的变化率时,也就引出了方向导数的定义,即:某一点在某一趋近方向上的导数值。
通俗的解释是:
我们不仅要知道函数在坐标轴正方向上的变化率(即偏导数),而且还要设法求得函数在其他特定方向上(注意还是在平面上来考虑这个问题,不是空间上,这在【动态展示】需要注意)的变化率。而方向导数就是函数在其他特定方向上的变化率。
动态展示 方向导数与梯度的关系--》方向导数=梯度与方向向量的内积=\((f_x,f_y)\cdot(con\alpha,cos\beta)=\Delta f \cdot \overrightarrow{\tau^0}=||\Delta f|| \cdot||\overrightarrow{\tau^0}|| \cdot cos\theta\),所以说当方向向量与梯度方向一致时,便是方向导数的最大值。
5.2 一元函数举例
5.1中讲解了梯度的有关概念,那么我们先以一元函数为例,讲解什么是梯度下降。
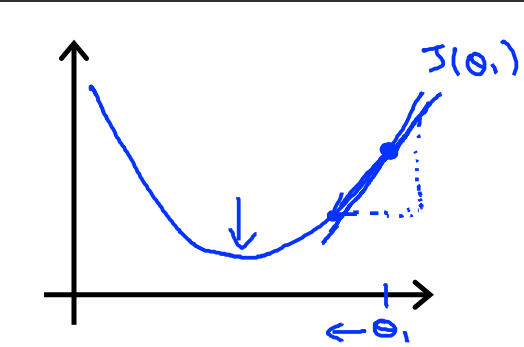
假设Cost function为\(J(\theta_1)\),其中\(\theta_1\)起初在最小值的右边,此时对函数求导,可以得到一个斜率为正数的切线。套用如下的公式,可以发现\(\theta_1\)是不断减小的
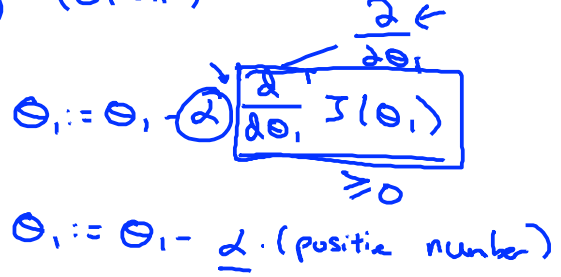
同理,我们假设\(\theta_1\)一开始在最小值的左边的时候,那么\(\theta_1\)是不断变大的。
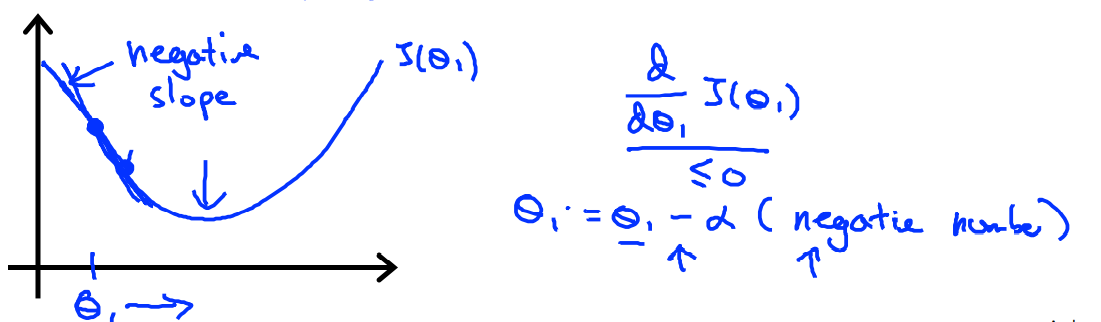
接下来用如下所示的图说明什么learning rate ——\(\alpha\)取值大小的作用。
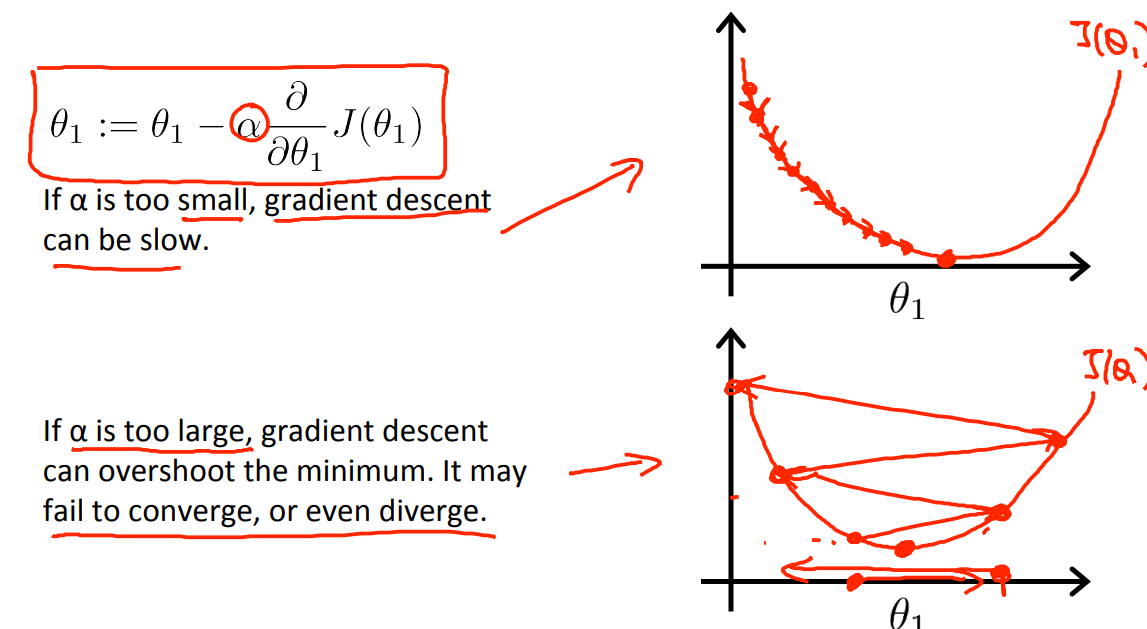
当我们接近局部最优解的时候,导数变得越来越小,甚至接近于0,那么移动距离也会变得越来越小,效果如下所示:
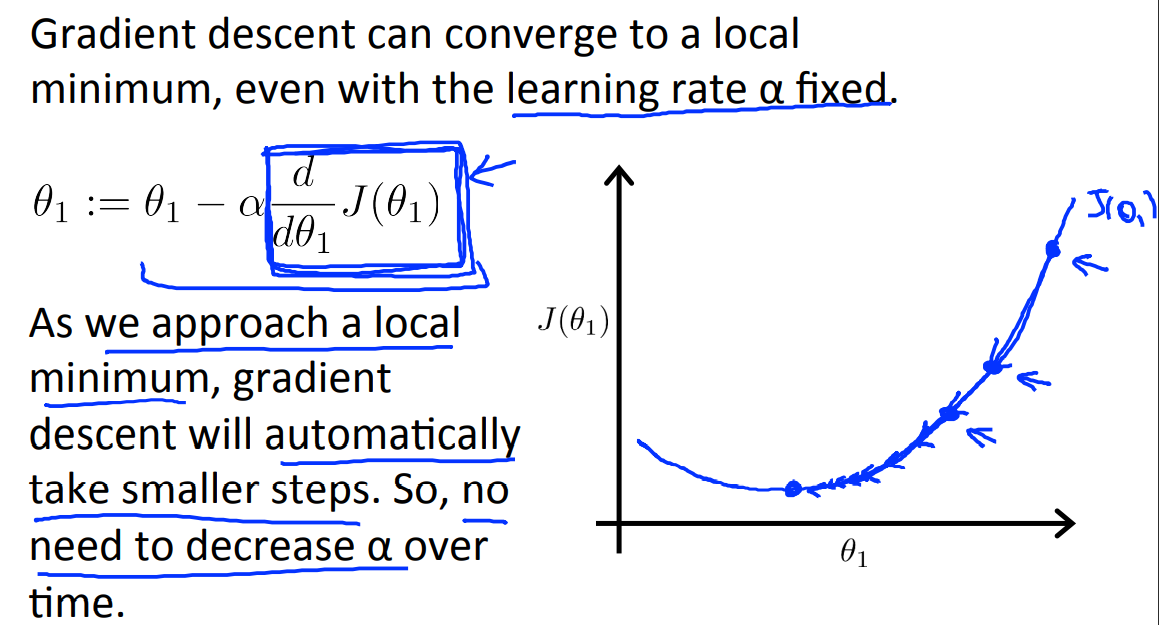
5.3 线性回归的梯度下降
那么接下来要做的就是要把梯度下降应用到定义的Cost Function当中去,然后得出我们想要的linear regression model;

将上图中的公式进一步展开,显式地表达如下图所示:

5.4 多元梯度下降法
这一部分主要是来说明如何利用梯度下降法来处理多元线性回归
假设函数Hypothesis: \(h_\theta(x)=\theta^Tx= \begin{bmatrix}\theta_0&\theta_1&\theta_2···\theta_n\end{bmatrix} \begin{bmatrix}x_0\\x_1\\x_2\\···\\x_n\end{bmatrix}=\theta_0x_0+\theta_1x_1+\theta_2x2+···+\theta_nx_n\)
其中参数\(\theta\)是我们要求的参数,这里就用n+1维的vector来表示,那么对其分别求偏导数,结果如下图所示:

这里约定令\(x_0=1\)
5.5 梯度下降法的优化方法
5.5.1 Scale Features特征缩放
我们假设一个二元函数,即\(h_\theta(x)=\theta_1x_1+\theta_2x_2\),对其进行模型的构建,假设\(x_1\in[0,2000],x_2\in[1,5]\),那么可以画出等高线图如下:
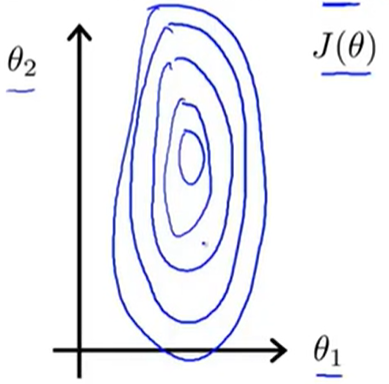
那么我们对其进行梯度下降的计算,路径用红色的线表示如下:
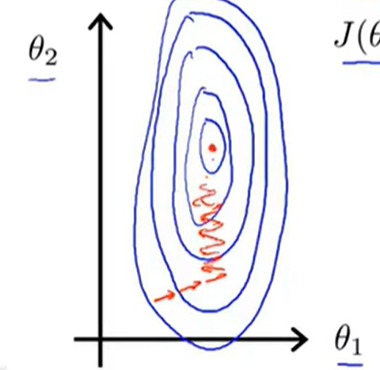
显然由于x的取值范围,导致了这样的结果,因此这样的求解过程就会显得特别的慢,收敛速度不好。
因此有一种有效的方法——scale features(特征缩放),具体的做法就是:
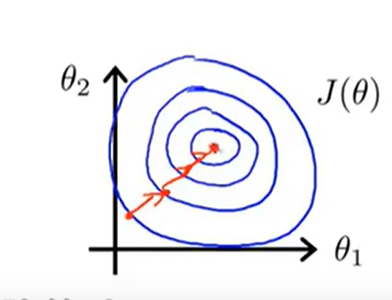
通常情况下,特征缩放的范围接近值是在\(-1<=x_i<=1\)这个范围就可以接受,比如\(0<=x_1<=3,-2<=x_2<=0.5\)这些都是可以接受的特征值,但是如说范围是在[-100,100]或者[-0.00001,0.001]这样极端的情况下,就需要抛弃这样的特征是。
吴恩达认为如果是在[-3,3]和[-1/3,1/3]的时候是可以接受的范围。
Mean normalization:Replace \(x_i\)with \(x_i-u_i\) to make features have approximately zero mean, in which the \(u_i\) is the average value of \(x_i\) in the training sets.
For example:
$ x_1=\frac{x_1-1000}{2000},x_2=\frac{x_2-2}{5} $这样的话-0.5<=x_1<=0.5 ,-0.5<=x_2<=0.5
5.5.2 \(\alpha\)学习率
在进行梯度下降的过程中,需要判断当前的情况是否正常工作,因此会有如下图所示的坐标图(纵坐标表示Cost Function,横坐标表示迭代次数):
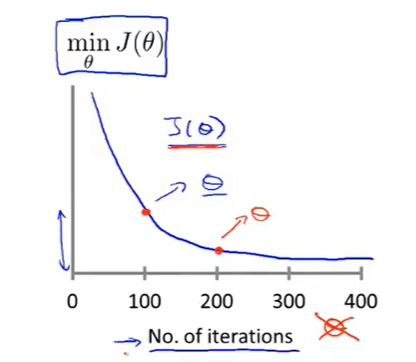
比如红色的两个点,分别表示迭代100次与200次时函数值
那么这条曲线可以很好地去直观判断当前的下降情况,即是否是处于收敛的状态(当然不同的函数,收敛的次数是不一样的,有可能100次就收敛了,有可能10000次才收敛)。
除了通过图象判断是否是收敛,还可以通过设定一个阈值\(\varepsilon\),如果cost Function两次的差值小于该阈值,也可判断是收敛。
但是如果得到的图像如下图所示:
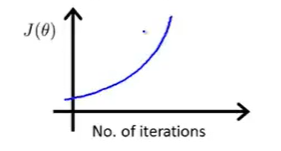
这表明下降法没有正常工作,需要使用更小一些的学习率\(\alpha\),这是因为如果一开始设定的学习率太大,那就有可能是在下面红色点开始进行梯度下降:
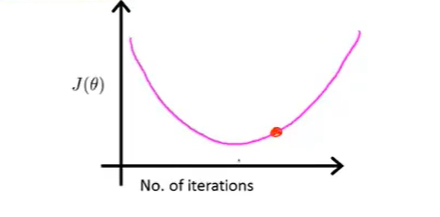
那么接下来的情况就是反复横跳的结果了:
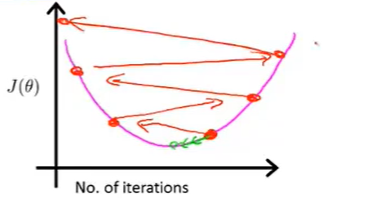
总得来说:
- if \(\alpha\) is too small --> slow convergence.
- if \(\alpha\) is too large --> cost function may not decrease on every iteration or may not converge
6. Normal equation正规方程
6.1 introduction
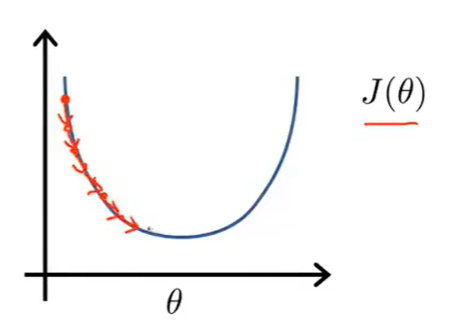
根据gradient decent梯度下降法可知,需要不断去进行迭代计算才能收敛到全局最小值(converge to the global minimum).
然而normal equation可以提供一种解析方法,使我们不用去进行迭代计算,便可以一步算出最优的\(\theta\)值。
假设\(J(\theta)=a\theta^2+b\theta+c\)来说,可以对函数求导数,便可以求出最小值的点。但是现实情况下,\(\theta\)不是一个值,而是一个向量,也就是说\(J(\theta_0,\theta_1,...,\theta_m)=\frac{1}{2m} \sum\limits_{i=1}^m (h_\theta(x^i)-y^i)^2\)需要对\(\theta_0,\theta_1,...\theta_n\)进行求偏导数(这里默认取\(x_0=1\))。
这是一个很常规的办法,那么在计算上可能就过于繁琐了,因此normal equation就是可以来一步解决这个问题。
还是举例,假设m=4,也就是说有数据集的大小为4,数据内容如下:
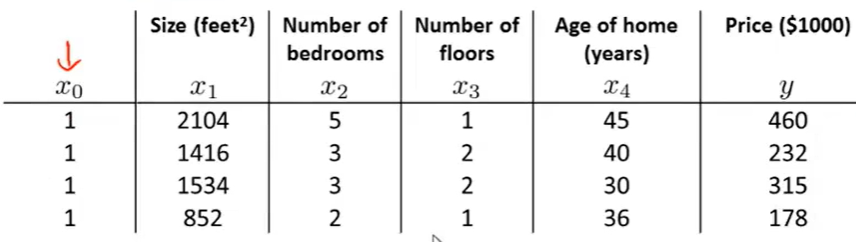
那么我们可以构建如下的矩阵:

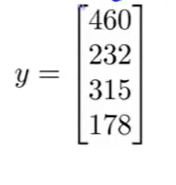
X矩阵(m*(n+1))中的每一行都是一个数据(包含了5个特征),y矩阵(m*1)就是对应的预测值。那么我们就可以得出:
$ \theta=(XTX)X^Ty $(先不要管什么可逆的问题,在[8.3](##8.3 Regularized linear regression)讲)
在广义化来说,有m个数据\((x^{1},y^1),...,(x^n,y^n)\);n个特征,其中\(x^i=\begin{bmatrix}x_0^i\\x_1^i\\...\\x_n^i\end{bmatrix}\),那么\(X=\begin{bmatrix}x^{1T}\\x^{2T}\\...\\x^{nT}\end{bmatrix}\) 。
也就是说,如果令\(\theta\)等于上式,那么这个\(\theta\)就会最小化线性回归的代价函数\(J(\theta)\)。
同时在使用normal equation的时候,不必使用了feature scale 来进行归一化的处理。
但是其有一些缺点也有一些优点需要我们注意。
| Gradient Descent | Normal Equation |
|---|---|
| need to choose \(\alpha\) | no need to choose \(\alpha\) |
| need many iterations | don't need to iteration |
| works well even when n is large | need to compute \((X^TX)^{-1}\)(\(O^3\)) |
| slow if n is very larg(n>1e6) |
因此需要根据情况来决定是使用normal equation还是gradient descent,小数据可以去使用了normal equation,但是相比于gradient descent来说,gradient descent应用的场景更多,使用的情况也是比较多的。例如在分类算法中,会遇到甚多的复杂算法,这时候normal equation就不再适用了。
6.2 non-invertible
根据公式\(\theta=(X^TX)^{-1}X^Ty\),可能会存在着\((X^TX)^{-1}\)是一个non-invertible(不可逆称之为singular/degenetate)
比如当m=10,n=100的时候,会导致矩阵不可逆;出现两个线性相关的变量;
那么通常的办法就是:1)删除一些特征;2)或者使用regulation(正规化)
7. Classification
分类问题的结果集可以看做只有0和1,即\(y\in\{0,1\}\),如何进行分类呢?
我们假设存在着一个线性回归函数,可以将肿瘤分类的结果(良性与恶性)划分为两个部分,结果如下图所示:
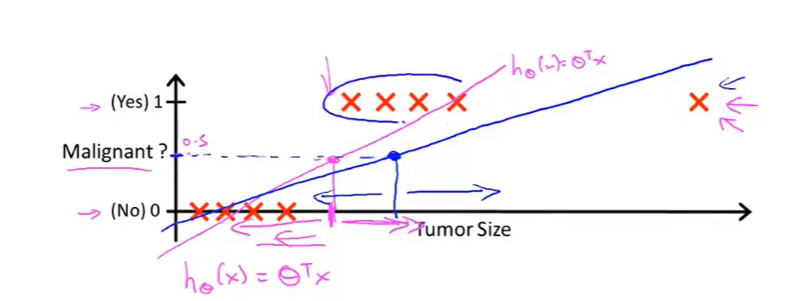
假设当阈值小于0.5的时候,认为y=0;当阈值大于等于0.5的时候,认为y=1;
此时我们觉得这个线性函数还不错,可以进行分类的工作。
但是如果再添加一个边缘数据,得到的线性回归函数的效果图如下所示:
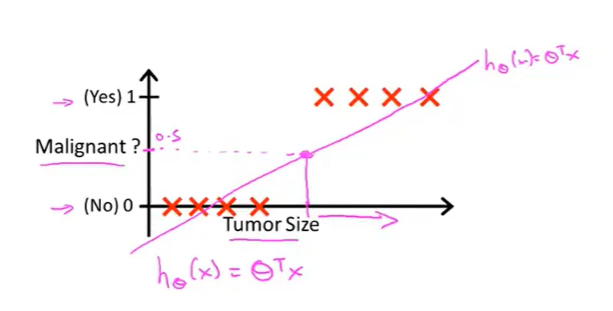
你会发现,如果还是根据h(x)大于等于某一个阈值来判断,效果却非常的差劲。
因此我们认为linear regression线性回归函数不适合进行分类的工作。
因此出现了一个新的算法——logistic regression(虽然有regression,但是与回归函数相关不大,这是历史遗留的问题)
7.1 Logistic regression
由前面介绍可知,分类问题的结果是在[0,1]之间的,因此Logistic regression的取值范围应也是在[0,1]之间的。
我们设\(h_\theta(x)=g(\theta^Tx),g(z)=\frac{1}{1+e^{-z}}\),其中\(g(z)=\frac{1}{1+e^{-z}}\)是Sigmoid function,也可以叫做Logistic function,两种叫法是等价的。
Sigmoid function的函数图像如下图所示:
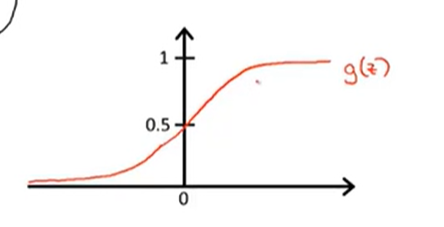
可以看到取值范围正好是在[0,1]之间的。
这里的Hypothesis假设函数\(h_\theta(x)\)的意义就是输入值x,输出值是1的可能性的大小。其实就是条件概率。
7.2 Decision boundary
由7.1可知,我们的假设函数为\(h_\theta(x)=g(\theta^Tx),g(z)=\frac{1}{1+e^z}\):
- predict "y=1" if \(h_\theta(x)>=0.5\)
- predict "y=0" if \(h_\theta(x)<0.5\)
从图像上来看,当x<0的时候,\(h_\theta(x)<0.5\);当x>=0的是\(h_\theta(x)>=0.5\)。
现在假设有一个如下图所示的训练集:
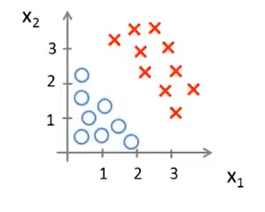
设Hypothesis=\(h_\theta(x)=g(\theta_0+\theta_1x_1+\theta_2x_2)\),假设现在已经拟好了参数,即\(\theta_0=-3,\theta_1=1,\theta_2=1\)。
依据上述提到的,当\(x<0时,预测值为0,当x>=0时,预测值为1\),在训练集中那就是\((-3+x_1+x_2)<0,预测值为0,(-3+x_1+x_2)>=0,预测值为1\),也就是说对于任何数据,只要是满足\(x_1+x_2<3\),那么就是0,反之为1,在图像上进行表示就是如下图所示(圈表示负样本,叉表示正样本):
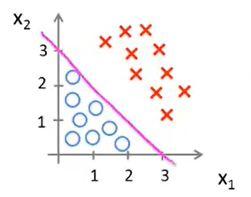
图中那条\(x_1+x_2=3\)的直线就叫做decision boundary。定义直线上方的区域就是y=1的区域,定义直线下方的区域就是y=0的区域。
注:decision boundary、y=1和y=0的区域它们都是hypothesis的属性,取决于其参数,不是数据集的属性,也就是说一旦确定了\(\theta^T\),那么就确定了decision boundary。训练集不是用于确定边界的,而是用于拟合参数的,从而参数确定了decision boundary。
那么接下来看一个更复杂的例子:
假设存在如下图所示的数据集(圈表示负样本,叉表示正样本):
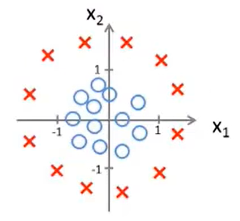
早期提到过polynomial regression多项式回归,也就是在feature特征中添加extra higher order polynomial terms高阶多项式来实现更加复杂的图像,因此在logistic regression也可以用这样的方法。
设\(h_\theta(x)=g(\theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_1^2+\theta_4x_2^2)\),其中参数分别为-1,0,0,1,1,那么最终的效果图如下所示:

7.3 cost function
在7.2中所提到的hypothesis中的参数是怎么得到的呢?
具体来说需要定义optimization objective 或者 cost function来实现拟合参数。
下图就是监督学习中logistic回归模型的拟合问题:

在线性回归中定义的cost function为\(J(\theta)=\frac{1}{m}\sum \limits_{i=1}^m cost(h\theta(x^i),y^i),cost(h\theta(x^i),y^i)=\frac{1}{2}(h_\theta(x^i)-y^i)^2\).
上述的cost function在线性回归中能够起到很好的效果,但是在logistic regerssion中效果就不是那么好了,原因是损失函数的局部最优太多,或者说是太密集,其损失函数的图像如下图所示:
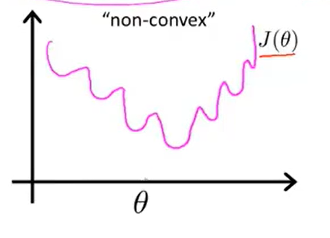
这就是一个“non-convex”非凸函数,如果是在这样一个图像上运用梯度下降法是很难获得最优解的,不能够保证能够收敛到全局最优解处。
下图所展示的就是我们定义的一种新的cost function函数:
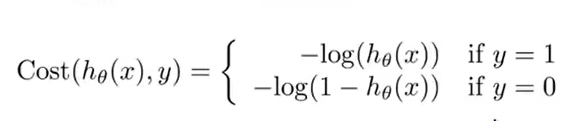
先看当y=1的部分图像:
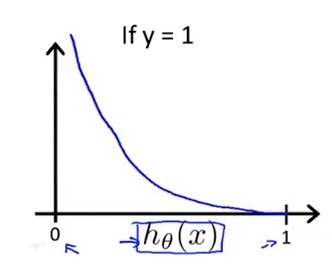
当\(h_\theta(x)=1,y=1\)的时候,此时损失函数的值为0,也就是说预测的效果是好的,当\(h_\theta(x)=0\)的时,损失函数-->∞。
当y=0时的图像如下图所示:
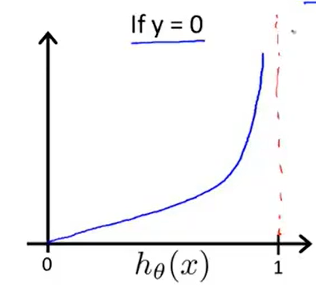
7.4 simplify cost function & gradient descent

对于上面的logistic regression 的损失函数的表达过于繁琐,可以进行优化合并两个表达式如下:
通过化简之后,便可以应用梯度下降法了:

其中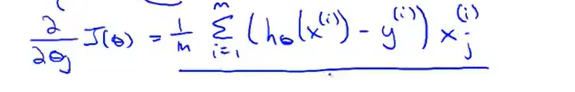 (推导的时候记得要将\(h_\theta(x)\)展开为\(\frac{1}{1+e^{-\theta^Tx}}\))
(推导的时候记得要将\(h_\theta(x)\)展开为\(\frac{1}{1+e^{-\theta^Tx}}\))
仔细观察会发现logistic regression的梯度下降的表达式与linear regression的梯度下降法的表达式是类似的(如果不考虑logisitic regression中求导之后的系数1/m的话,可以认为是相同的)

因此和linear regression一样,可以利用scale feature来保证其收敛的。
7.5 Advanced optimization
前面一直在介绍梯度下降法,其实在很多的大数据或者说大规模的情况下,梯度下降法可能就不是一个很好的选择了,因此需要有一些更加高级的优化算法来是实现这些操作:
- Conjugate gradient
- BFGS
- L-BFGS
上述是三种方法既有优点,同时也有缺点:
Adventage:
- No need to manually pick \(\alpha\)(学习率)
- Often faster than gradient decent
Disadvantage:
- More complex
通常在使用的时候,是通过使用各种封装好的库中进行调用就好。
吴恩达也表示自己更多情况下也是使用了高级的优化方法,而非使用梯度下降法。
7.6 Multi-class classfication: One-versus-All
在7.1中的引例是使用了恶性肿瘤的分类判断,那么相对来说比较简单。
但是还是有很多复杂的分类情况,比如:

在两种情况的时候,我们可以通过计算找到decision boundary,那么分类两种以上的情况下,该如何进行呢?
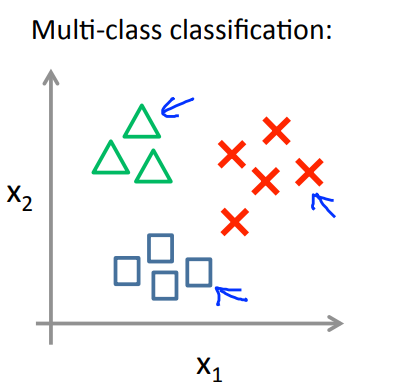
那就采用One-ve-All即一对多的处理方法思想,有时也被称作one-vs-rest。
那么假设要进行三种情况的分类,三角用y=1代表,方块用y=2代表,叉号用y=3代表。
先以三角为例:
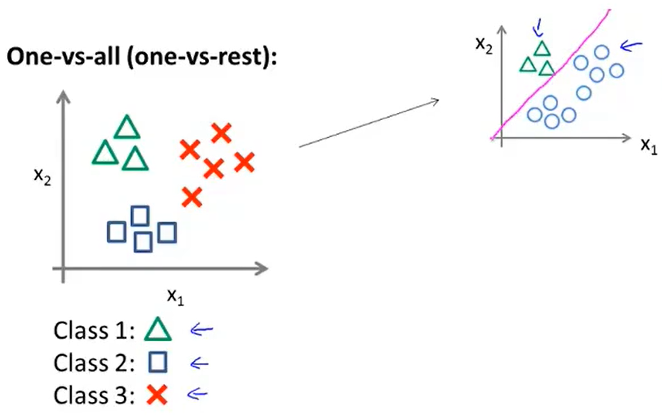
我们将三角认为是正样本,其余的都看做是负样本,此时便可以得到分界线,同样的方法,可以应用于剩下的:
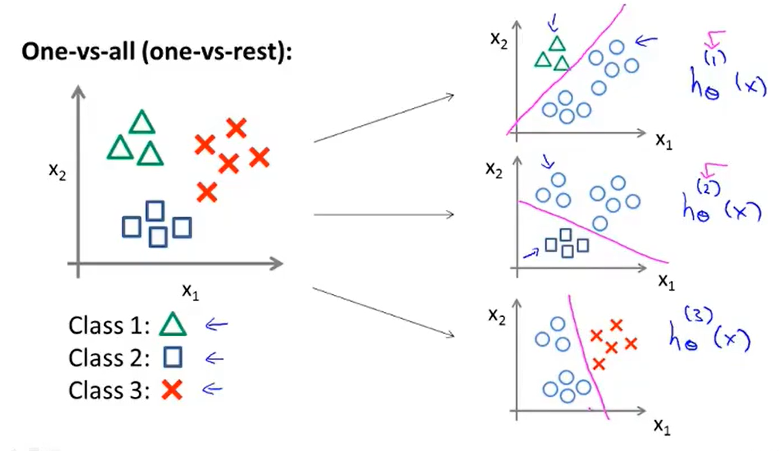
那么就可以得到三个分类器\(h_\theta^i(x)=P(y=i|x;\theta)\)(给定x和参数\(\theta\)便能估计出y=i的可能性大小)。
每个分类器都针对其中一种情况进行训练,便得到拟合好的参数了。
总结来说:
- 针对不同的分类,可以获得不同的分类器\(h_\theta^i(x)=P(y=i|x;\theta)\)来预测各自的可能性;
- 对于给定的需要预测的x,选择出概率最大的便是最后的结果,即\(max{P(y=i|x;\theta)}\)
8. The problem of overfitting
8.1 introduction
在linear regression和logistic regression都会存在过拟合的问题。
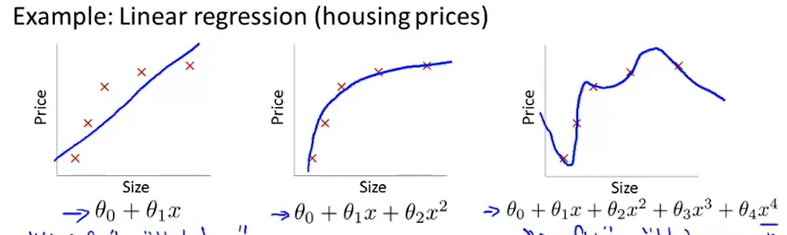
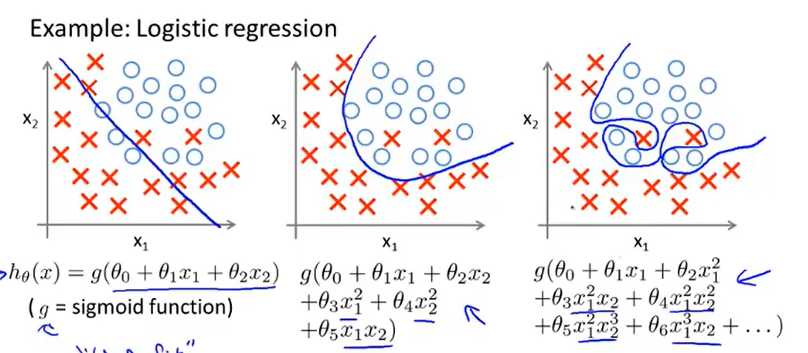
最左边的都是underfitting,最右边的是overfitting。
过拟合就会导致在新的数据出现的时候,不能够很好地去预测。
过拟合也有两种方法去解决:
-
减少特征的数量
-| 手动选择需要留下那些重要的特征,删去非必要的特征;
-| 模型选择算法--该算法可以动态去选择留下哪些特征;
-
regularization正则化
-| 会保留所有的特征,但是会降低参数\(\theta\)的数量级和大小;
-|Works well when we have a lot of features, each ofwhich contributes a bit to predicting y.
8.2 what's the regularization
由8.1知导致过拟合的问题之一就是参数的数值或者说数量级的问题,因此在此要进行数量级的消减。
我们假设是\(\theta_3和\theta_4\)导致了过拟合,那么就对cost function做一些更改操作——“惩罚”参数
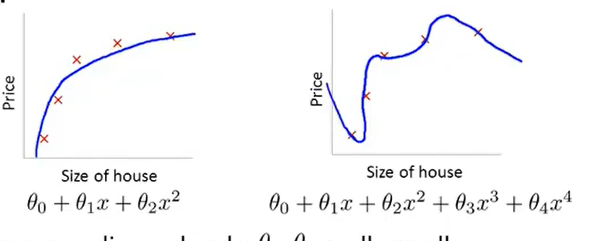
这样就会导致\(\theta_3和\theta_4\)在梯度下降的过程中趋于0,从而解决了overfitting的问题。
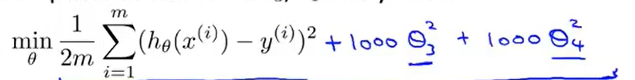
结果表明,数值越小,曲线就会越平滑,因此也就不会导致overfitting。
但是在实际过程中是不知道到底是哪些参数导致了overfitting,因此需要对全体的参数进行“惩罚”。
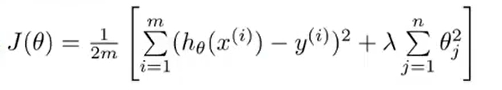
上式中\(\lambda\)是regularization parameter 。但是如果这个参数过大,就会导致除了\(\theta_0\)之外的所有参数都会是0。(至于上式中为何是从j=1开始,其实这是一个约定俗成的写法,其实从j=0开始也是没有问题的)
因此在regularization过程中要选择正确合适的参数才可以的,在后面会讲到自动选择这个参数值。
8.3 Regularized linear regression
这一节会从公式的角度上来说明为什么regularization之后的结果是可以收敛的——从gradient descent和normal equation两个用于拟合linear regression的方法。
根据正则化之后的损失函数,可以写成\(J(\theta)=\frac{1}{2m}[\sum \limits_{i=1}^m(h_\theta(x^{(i)})-y^{i})^2+\lambda\sum\limits_{j=1}^n\theta_j^2]\)。
那么根据梯度下降法,只需要对参数求偏导即可:
Repeat{
$$\theta_0=\theta_0-\alpha\frac{1}{m}\sum \limits_{i=1}m(h_\theta(x)-y{i})x_0$$
$$\theta_j=\theta_j-\alpha[\frac{1}{m}\sum \limits_{i=1}m(h_\theta(x)-y{i})x_0-\frac{\lambda}{m}\theta_j]$$
}
那么对第二个式子进一步展开和并便能得到如下的式子:
其中\(1-\alpha\frac{\lambda}{m}\)是小于并且接近1的小数,也就是说类似于0.99、0.98这样的小数,因此可以看出\(\theta\)是不断减小的。
那么在normal equation中,我们用如下的式子来表示:
其中矩阵是一个(n+1)*(n+1)维的。
在6.1中留下了一个问题,就是矩阵是否是可逆的,当时确实是不能够判断是否是可逆的,尤其是当m<=n的时候:

但是如果加入了上述的矩阵,那么就可以保证矩阵的可逆性了。
8.4 Regularized logistic regression
由[7.4](##7.4 simplify cost function & gradient descent)可以知道损失函数的写法和利用梯度下降法所得到的结果:

那么同样的对\(J(\theta)\)进行regularization可以得到:
\(J(\theta)=-[\frac{1}{m}\sum\limits_{i=1}^my^{(i)}logh_\theta(x^{(i)})+(1-y^{(i)})log(1-h_\theta(x^{(i)}))+\frac{\lambda}{2m}\sum\limits_{j=1}^n\theta_j^2]\)
求偏导数之后的结果如下:
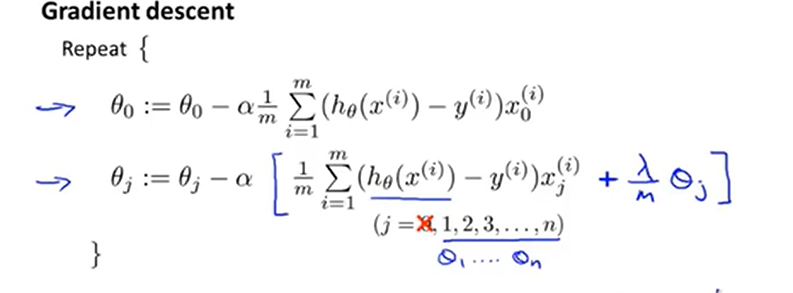
会发现与linear regression的结果是一样的,不一样的就是此处的\(h_\theta(x)=\frac{1}{1+e^{-\theta^TZ}}\)
9. Non-linear hypothesis
9.1 introduction
我们已经有了linear regression和logistic regression,为什么还要有Non-linear hypothesis呢?
假设对于只有两个特征的分类,可以用logistic regression来实现分类:
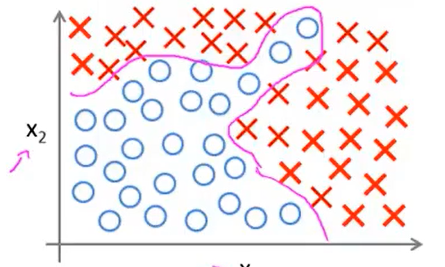
还是以预测房子的价格为例,如果特征值有100种:

那么一开始所计算出的hypothesis会很复杂,光是二次项(\(x_1^2,x_1x_2,x_1x_3,x_1x_4,...,x_1x_{100},x_2x_3,...,x_2x_{100}\))就接近有5000项(呈现\(O(n^2)\)的数量级)。
在处理那么多的特征值的时候,一方面有可能会导致overfitting的问题;另一方面就是计算量过大。
那么还有三次项(\(x_1^3,x_1^2x_2,...,x_1x_2x_3,...\))的数量更是多,大约有17000项。
但是对于实际的机器学习的过程,the n of feature is vary large。
再举一个例子:
计算机视觉中有汽车识别的问题,我们假设选取的图片大小为50*50pixel(下图中的pixel1和pixel2都是像素值为1 的像素点),那么特征空间的大小为50*50大小,
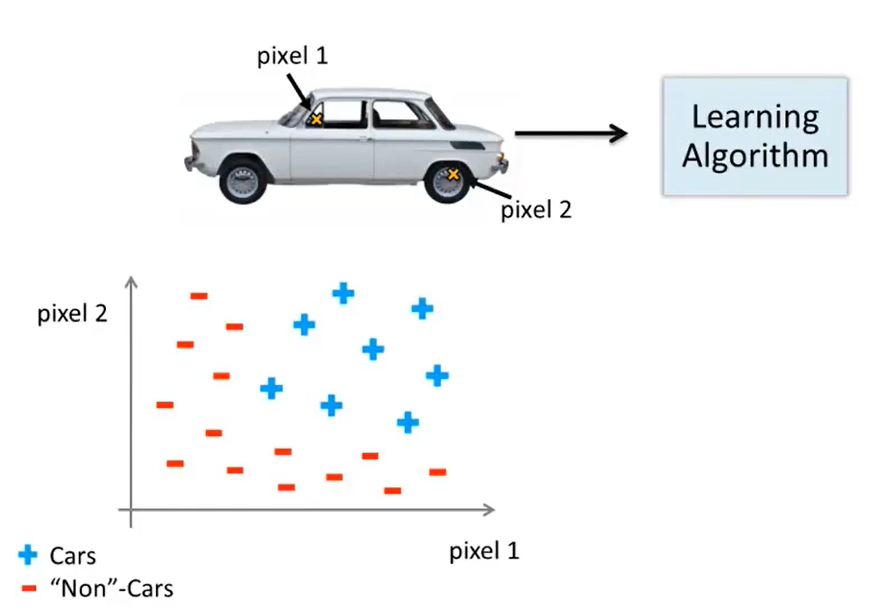
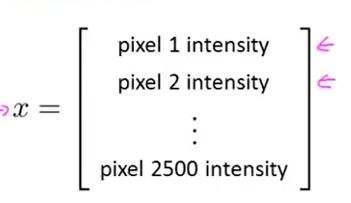
对于灰度图,那么特征数量就是n=2500,但是如果是RGB图像,那此时的n=2500*3=7500个特征值。
如果对于一个只包含二项式的hypothesis来说,那么需要训练的参数值就达到接近3million 。
因此,如果说n很大的时候,并且是包含了二次项和立方项的式子,用logistic regression来fit参数不是一个好的方法,计算量特别大,因此便引入了neutral network——可以解决复杂的nonlinear hypothesis 。

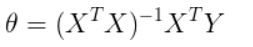

 浙公网安备 33010602011771号
浙公网安备 33010602011771号