概率论与统计

这一篇文章纯粹就是偶然想写的。

因为今天在学习机器学习的时候，突然被一个概念——协方差给困住了，那么在查看的时候，又出现了方差的概念。

对于方差这个概念，我们小学或者中学就学过了，不就是每一个样本减去均值的和处于样本总数嘛，用公式表示就是\(\sigma=\frac{\sum_{i=1}^n(x-\mu)}{n}\),其中\(\mu\)是均值;

当然这是方差的定义，我不可能专门为此专门写一篇文章的，我的问题在于，随着学习的深入我遇到了方差还有其他的表示方法：

\(S^2 = \frac{1}{n-1}\sum_{i=1}^n(x_i-\bar{X})^2\)​​

我就开始好奇了，为什么一个是n一个是n-1呢？

这就让我对大学学到一门课程叫做《概率论与数理统计》有了更加深一步的理解与认识，所谓的《概率论与数理统计》是两个概念，一个是概率论，一个是叫做数理统计。

仔细想想这本书，前3/4的部分都是在讲解概率论的知识也就是我们学过的概率论的八大概率分部。

后面的1/4的部分就是数理统计的知识范畴了。

那么概率论与统计之间的关系是什么？

来自于微博的一张图：

img

The basic problem that we study in probability is:
Given a data generating process, what are the properities of the outcomes?
...
The basic problem of statistical inference is the inverse of probability:
Given the outcomes, what can we say about the process that generated the data?

img

​ A Brief Introduction to Probability & Statistics – BetterExplained

举个例子就是：

概率论研究的是一个白箱子，你知道这个箱子的构造（里面有几个红球、几个白球，也就是所谓的分布函数），然后计算下一个摸出来的球是红球的概率。而统计学面对的是一个黑箱子，你只看得到每次摸出来的是红球还是白球，然后需要猜测这个黑箱子的内部结构，例如红球和白球的比例是多少？（参数估计）能不能认为红球40%，白球60%？（假设检验）

而概率论中的许多定理与结论，如大数定理、中心极限定理等保证了统计推断的合理性。做统计推断一般都需要对那个黑箱子做各种各样的假设，这些假设都是概率模型，统计推断实际上就是在估计这些模型的参数。

有了这些概念的铺垫之后，再次简单回顾总结一下概率论中方差计算方法：

  • 统计中方差的一般表述形式(也称为总体方差)：\(S^2=\frac{\sum_{i=1}^n(x-\mu)}{n}\)​
    • 离散型方差的一般形式：\(DX = \sum_{i=1}^n(x_i-EX)^2p_i\)
    • 连续型方差的一般形式：\(DX = \sigma^2=\int_{-\infty}^{\infty}(x-EX)^2 f(x)dx=E(x^2)-E(X)^2\)​
  • 数理统计中方差的一般形式(也称为样本方差)：\(S^2 = \frac{1}{n-1}\sum_{i=1}^n(x_i-\bar{X})^2\)​

这里的\(\bar{X}\)和\(\mu\)一般来说是不相等的，因为\(\bar{X}\)是一组样本中的均值，也成为样本均值，不是真正的均值，因为样本方差求的就是一个估值，统计学就是根据数据推断概率模型，因此用\(\bar{X}\)来表示均值。

那么接下来就回到一开始提出的问题：

为什么样本方差是除以n-1而不是n呢？

首先我们知道样本方差也在其他的地方叫做无偏估计，为什么叫做无偏就要跟这次讨论的问题有关了。

首先样本的均值\(\mu\)是未知的，因为只有数据是很难看出符合什么概率分布的，但是我们可以求出均值\(\bar{X}\)。

那就有一个可以从数学上证明的结论：

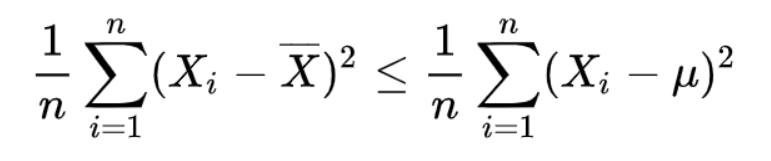
image-20210831205602058

当且仅当\(\bar{X}=\mu\)的时候等号才成立；

那么既然是小于等于，是不是可以将不等号左边的式子的分母变大一些就可以了呢？

事实上就是变大了：

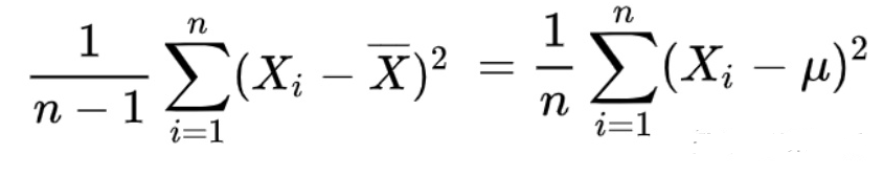
image-20210831205818813

接下来就是严格的数学推导，为什么分母不是n-2，n-3，而是n-1；

那么此时根据方差的定义，如果不加修改直接套用的话，可以得出：

\(\begin{align}S^2 &=\frac{1}{n}\sum_{i=1}^n(X_i-\bar{X})^2 \\ &=\frac{1}{n}\sum_{i=1}^n(X_i-\mu+\mu-\bar{X})^2 \\ &=\frac{1}{n}\sum_{i=1}^n(X_i-\mu)^2+\frac{2}{n}\sum_{i=1}^n(X_i-\mu)(\mu-\bar{X})+\frac{1}{n}\sum_{i=1}^n(\mu-\bar{X})^2 \\ &= \frac{1}{n}\sum_{i=1}^n(X_i-\mu)^2+2(\bar{X}-\mu)(\mu-\bar{X})+(\mu-\bar{X}) \\ &= \frac{1}{n}\sum_{i=1}^n(X_i-\mu)^2-(\mu-\bar{X})\end{align}\)​​​

当\(\mu=\bar{X}\)​​的时候才认为是\(\frac{1}{n}\sum_{i=1}^n(x_i-\mu)^2=\frac{1}{n}\sum_{i=1}^n(x_i-\bar{X})^2\)​​，否则一定有\(\frac{1}{n}\sum_{i=1}^n(x_i-\mu)^2 <\frac{1}{n}\sum_{i=1}^n(x_i-\bar{X})^2\)​​

这样就说明了使用n会导致偏差的出现。

image-20210901115313137

那么接下来就是分析为什么是使用n-1，再搞懂之前需要知道以下的一些性质。

  • \(D(X)=E(X-EX)^2=E(X^2-2XE(X)+(EX)^2)=E(X^2)-(E(X))^2\);
  • 设X1,X2,X3,....独立同分布，则满足\(E(X_i)=\mu,D(X_i)=\sigma^2\);
  • 由\(\bar{X}=\frac{1}{n} \sum_{i=1}^nX_i\)
    • \(E(\bar{X})=\frac{1}{n}\sum_{i=1}^nE(X_i)=E(X)=\mu\);
    • \(D(\bar{X})=\frac{1}{n^2}\sum_{i=1}^nD(X_i)=\frac{\sigma^2}{n}\)

要想实现无偏估计必须有\(E(S^2)=E(\sigma^2)=\sigma^2\)​

这里的总体方差\(\sigma^2\)​是真正的方差，\(\sigma^2=\frac{1}{n} \sum_{i=1}^2(X_i-\mu)^2\)​

\(\begin{align}E(S^2) &=E(\frac{1}{n}\sum_{i=1}^n(x_i-\bar{X})^2) \\ &= E(\frac{1}{n}\sum_{i=1}^n(x_i^2-2x_i\bar{X}+\bar{X}^2)) \\ &= E(\frac{1}{n}\sum_{i=1}^nx_i^2)-E(\bar{X}^2) \\ &= E(X^2)-E(\bar{X}^2) \\ &= D(X)+(E(X))^2-D(\bar{X})-(E(\bar{X}))^2 \\ &= \sigma^2+\mu-\frac{\sigma^2}{n}-\mu \\ &= \frac{n-1}{n}\sigma^2\end{align}\)​

那么：

\(\begin{align}\frac{n}{n-1}E(S^2) &=\frac{n}{n-1}*\frac{n-1}{n}\sigma^2\\ &=\sigma^2 \\ &=\frac{n}{n-1}E(\frac{1}{n}\sum_{i=1}^n(X_i-\bar{X})^2) \\ &=E(\frac{1}{n-1}\sum_{i=1}^n(X_i-\bar{X})^2) \end{align}\)

到这里就可以看出只要\(S^2=\frac{1}{n-1}\sum_{i=1}^n(X_i-\bar{X})^2\)，那么样本方差就成为是无差估计。

posted @ 2024-06-05 17:03  昭建  阅读(44)  评论(0)    收藏  举报