dfs 序求 LCA！
前言
为什么用 dfs 序求 LCA 而不用欧拉序？
帅- 常数小，
也就一半 好玩
反正没什么正经理由。
正文
定义
- dfs 序是指对树进行深度优先遍历后得到的节点序列。
- \(\mathit{dfn}_i\) 是节点 \(i\) 在 dfs 序中的位置（从 \(0\) 或 \(1\) 开始无影响）。
- LCA 是最近公共祖先。
- 深度 \(\mathit{dep}_i\) 表示 \(i\) 到根的距离（根深度为 \(0\) 或 \(1\) 无影响）。
- 某个点的子树是指该点及其所有后代。
性质
- dfs 序中，祖先出现在后代之前（显然的）。
做法 \(1\)
问：求点 \(u,v\) 的 LCA：\(l\)。一般来说 \(u\ne v\)。
解：
首先，显然可以设 \(\mathit{dfn}_u<\mathit{dfn}_v\)。不满足就 swap。
情况 \(1\)，\(u,v\) 位于 \(l\) 的孩子的不同子树内，即 \(u,v\) 无祖先后代关系
思路同欧拉序，考虑 \(\forall w\) 满足 \(\mathit{dfn}_w\in[\mathit{dfn}_u,\mathit{dfn}_v]\)。通过性质 \(1\)，得知 \(w\) 不可能为 \(l\)。
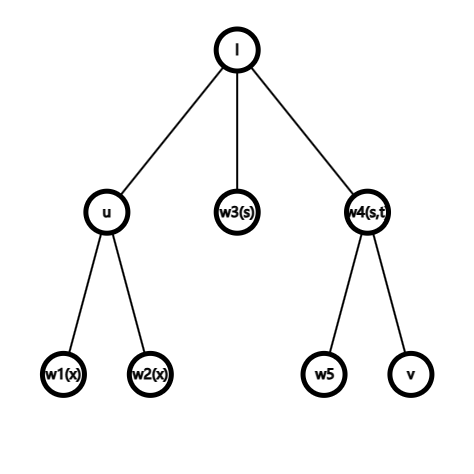
那么考虑 \(w\) 可以为那些点。
- \(u\) 的孩子。
- \(l\) 的一些孩子及其部分后代。
类型 \(1\) 的点与 \(l\) 的关系比 \(u\) 还远，可以舍去（(x)）。
由于与 \(l\) 关系最近的点即为 \(l\) 的孩子，所以考虑设它们中符合 \(w\) 条件的任意一个为 \(s\)。这种点必然存在，比如 \(l\) 的一个孩子 \(t\)，使得 \(t\) 的子树内有点 \(v\)。这样 \(t\) 可以为 \(s\)，且 \(t\) 符合成为 \(w\) 的条件。
考虑 \(s\) 的性质。由于它是 \(l\) 的孩子，所以 \(s\) 是 \(w\) 中深度最小的点之一。
即 \(s\) 可以为在 dfs 序中区间 \([\mathit{dfn}_u,\mathit{dfn}_v]\) 中任意深度最小的点。具体取到哪一个 \(s\) 并不重要，它们都是 \(l\) 的孩子。
解法就出来了。\(s\) 的父亲即为 \(l\)。
情况 \(2\)，\(u,v\) 互为祖先后代，即 \(v\) 为 \(u\) 的后代
考虑沿用原解法。不出意外地，那样会求到 \(u\) 的父亲去。事实上，\(l=u\)。如何解决？
特判显然可行，直接判断是否满足 \(\mathit{dep}_v-\mathit{dep}_u=\mathit{dfn}_v-\mathit{dfn}_u\) 即可。
但这样不够优美， 有没有更好的解决办法呢？
发现 \(t\ne u\)。因为若 \(t=u\)，则 \(u\) 为 \(v\) 的祖先，\(l=u\)，又因为 \(t\) 为 \(l\) 的孩子，推出 \(u\) 为 \(u\) 的孩子，矛盾。
所以即使在区间 \([\mathit{dfn}_u,\mathit{dfn}_v]\) 中排除 \(u\)，照样可以取到至少一个 \(s\)。同时因为排除了 \(u\)，就不会因为 \(u\) 深度最小而将 LCA 求到 \(u\) 的父亲去了。
那么可以将 \(w\) 满足的条件调整为 \(\mathit{dfn}_w\in[\mathit{dfn}_u+1,\mathit{dfn}_v]\)，完美解决！
使用 st 表解决即可。瓶颈在于 RMQ，可以做到 \(O(n)\sim O(1)\)。
做法 \(2\)
在做法 \(1\) 的基础上，考虑继续简化。（沿用上面的所有记号。）
注意到以下性质：
- \(l\) 是 \(l\) 的子树内 \(\mathit{dfn}\) 最小的点。
- \(w\) 的所有可能的点都在 \(l\) 的子树中。
由于上面的性质，\(w\ne l\)，故 \(w\) 的所有可能的点的父亲也都在 \(l\) 的子树中，且必然包括 \(l\)（\(s\) 可以为 \(w\)，\(s\) 的父亲为 \(l\)）。
又由于 \(w\) 的所有可能的点的父亲中 \(l\) 的 \(\mathit{dfn}\) 最小，故满足 \([\mathit{dfn}_u+1,\mathit{dfn}_v]\) 的点的父亲中 \(\mathit{dfn}\) 最小的点即为 \(l\)。这样甚至不用记录 \(\mathit{dep}\)，也不用开数组记录 \(\mathit{fa}\)，只需要在 dfs 是将 st 表初始值 \(\mathit{st}(0,i)\gets \mathit{fa}\) 即可。
后记
少量参考了 此文。
