网络流
最大流
知识点
定义:
- 网络:边有容量的有向连通图,其中只有一个点入度为 \(0\),一个点出度为 \(0\)。
- 原点:入度为 \(0\) 的点,记作 \(s\)。
- 汇点:出度为 \(0\) 的点,记作 \(t\)。
- 流量:记作 \(f(u,v)\)。
- 容量:通过一条边流量的上界,记作 \(c(u,v)\),即 \(f(u,v)\le c(u,v)\)。
- 残量:还可经过一条边的流量,即 \(g(u,v)=c(u,v)-f(u,v)\)。
- 最大流:单位时间经过汇点的最大流量。
性质:
- 流量守恒:\(\sum \limits_v f(v,u)=\sum \limits_v f(u,v)\)。
- 反对称性:\(f(u,v)=-f(v,u)\)。
Ford–Fulkerson 增广
如果存在一条 \(s\to t\) 的路径,使得每一条路径上的边 \((u,v)\) 都有 \(g(u,v)>0\),则称这样的路径为「增广路」。如果原图存在增广路,则一定可以使当前答案增加,因为路径上每条边的 \(f(u,v)\) 都可以加上 \(g(u,v)\) 的最小值;换句话,当前答案为最大流仅当不存在一条增广路。
因为具有后效性,所以为了「反悔」,对于边 \((u,v,c)\) 建立反向边 \((v,u,0)\)。用到反对称性,所以可以知道 \(g(v,u)=f(u,v)\),\(f(v,u)\) 是负数只是为了让 \(g(v,u)>0\) 从而实现反悔。
Edmonds–Karp 算法
每次从 \(s\) 开始 bfs 找 \(s\to t\) 的增广路 \(G\),同时求出 \(x=\min\limits_{(u,v)\in G}g(u,v)\)。然后将这条路上的残量进行更新,同时需要更新反向边的残量。当找不到增广路时停止。
因为一般图不选择这种做法,所以时间复杂度就不分析了,反正是 \(O(nm^2)\)。
Dinic 算法
我不会。
SAP 算法
主要思想是对原图进行「分层」。
对于 EK 算法,时间复杂度瓶颈在于每次都要重头去找增广路,而无法进行回溯。
所以我们从 \(t\) 开始 bfs,用 \(dis_u\) 表示 \(u\) 到 \(t\) 的最短距离。所以这样就将 \(dis\) 相同的分在了同一层。
求增广路采取深搜,记录当前点的入流量 \(in\),返回的是这个点的出流量 \(out\)。限制一个点只能去向下一层,即经过 \((u,v)\) 的条件仅当 \(g(u,v)>0\) 且 \(dis_u=dis_v-1\)。如果一个点出流量小于入流量\(^{1}\),那么它就要上一层,因为对于这个点来说,它下一层的点肯定已经满流了,只能上一层去分流。所以让 \(dis_u=dis_u+1\)。在深搜的过程中就已经将残量更新,当到 \(t\) 的时候,说明已经找到增广路。
在枚举边的时候,如果出流量已经等于入流量或者已经找不到增广路,便可以停止。
常见优化有两个。一个是用 \(cnt\) 数组记录第 \(i\) 层的点数,那么如果存在断层即 \(cnt_i=0\) 或者 \(dis_s\ge n\),肯定是找不出增广路了的。其次是用当前弧优化,避免多次重复走一条无用边,然后在 \(dis\) 标记更改时重新复原。
建模
拆点
将经过一条点的次数限制转化成拆成两个点用容量进行限制。
首先显然网络流无法处理轮数,所以考虑直接二分答案 \(x\)。
很显然应该想到男孩看做点,女孩也看做点。考虑 \(k\) 的限制。相当于将男孩和女孩拆成 \(2\) 个点。\(u\to u'\) 走这条边就表示和不喜欢的跳舞,容量设为 \(k\)。那么对于男孩 \(i\) 和女孩 \(j\),如果 \(i\) 喜欢 \(j\),那么 \(i\) 直接连向 \(j'\),容量 \(\inf\);如果不喜欢,那么应该是 \(i'\) 连向 \(j\)。
原点分别连向 \(i\) 容量为 \(x\) 的边,\(j'\) 分别连向汇点容量为 \(x\) 的边,答案可行仅当满流。
行列
将行列互有影响的问题转换成最大流模型。
判断是否存在一个 \(n\times m\) 的矩阵,使得第 \(i\) 行的和为 \(h_i\),第 \(j\) 列的和为 \(g_i\),且数字大小在 \([0,x]\) 范围内。
考虑进行建模。开 \(n+m\) 个点表示行和列,原点向行 \(i\) 连容量为 \(h_i\) 的边,相当于限制这一行的和为 \(h_i\);列 \(j\) 向汇点连容量为 \(g_j\) 的边,相当于限制这一列的和为 \(g_j\)。考虑行和列的关系,\((i,j)\) 表示第 \(i\) 行第 \(j\) 列的数 \(y(\le x)\),相当于表示行 \(i\) 和列 \(j\) 有容量为 \(x\) 的边。那么如果能满流,也就表示有解。
如果限制为 \([l,r]\),因为 \((i,j)\) 的流量相当于第 \(i\) 行第 \(j\) 列的数,是 \([0,x]\) 范围的,所以考虑将原问题每个数减去 \(l\)。
交换
处理可交换问题。
有 \(n\) 个人,\(1\) 号可以拿自己的邮票跟其他人换,但对于被换人来说,拿出去的邮票必须有多张且拿到的邮票是自己没有的。问 \(1\) 号最多有几种邮票。
考虑对于邮票和人开点。首先如果 \(1\) 号有第 \(i\) 种邮票 \(s_i\) 张,那么源点向 \(i\) 连容量为 \(s_i\) 的边;每种邮票所对应的点向汇点连容量为 \(1\) 的边,统计答案。
对于第 \(k\) 个人,如果他有第 \(i\) 种邮票 \(j\) 张,如果 \(j=0\),那么 \(j\) 向 \(k\) 连容量为 \(1\) 的边,表示可以给他一张;如果 \(j>1\),那么 \(k\) 向 \(j\) 连容量为 \(j-1\) 的边,表示他可以给出这么多张。具体分配交给最大流自己搞。
最小割
知识点
- 割:将网络中的点分成两个集合 \(S\) 和 \(T\),其中源点 \(s\in S\),汇点 \(t\in T\)。记为 \(\text{CUT}(S,T)\)。\(\text{CUT}(S,T)\) 必须满足对于 \(i\in S\),\(s\) 必须可达 \(i\)(即在残量网络中,存在一条 \(s\) 到 \(i\) 且每条边的残量 \(>0\) 的路径),对于 \(i\in T\),\(i\) 必须可达 \(t\)。
- 割边:如果边 \((u,v)\) 满足两个点属于不同的集合,则这条边为割边。
- 正向割边:满足 \(u\in S\),\(v\in T\)。
- 逆向割边:满足 \(u\in T\),\(v\in S\)。
- 割的容量:所有正向割边容量之和。
最大流最小割定理
- 定理一:如果 \(f\) 是网络中从源点到汇点的一个流,\(\text{CUT}(S,T)\) 是任意一个割,那么 \(f\) 的值等于正向割边的流量与逆向割边的流量之差。
- 证明:由于 \(s\in S\),\(t\in T\)。所以对于正向割边的流量就是 \(s\) 流向 \(t\) 的流量,反之是 \(t\) 流向 \(s\) 的流量。
- 推论一:如果 \(f\) 是网络中从源点到汇点的一个流,\(\text{CUT}(S,T)\) 是一个割,那么 \(f\) 的值不超过割 \(\text{CUT}(S,T)\) 的容量。
- 证明:用 \(f(u,v)\) 表示正向割边的流量,\(g(u,v)\) 表示正向割边的容量,\(f=f(u,v)-f(v,u)\le f(u,v)\le g(u,v)\)。
- 推论二:网络中的最大流不超过任何割的容量。
- 证明:同理。
- 定理二:在任何网络中,如果 \(f\) 是从源点到汇点一个流,\(\text{CUT}(S,T)\) 是一个割,且 \(f\) 的值等于割 \(\text{CUT}(S,T)\) 的容量,那么 \(f\) 是一个最大流,\(\text{CUT}(S,T)\) 是一个最小割(容量最小的割)。
- 用推论二可证明。
- 最大流最小割定理:在任何的网络中,最大流的值等于最小割的容量。
- 证明:因为是最大流,所以原图不存在增广路。又因为割要求可达,所以对于每一条正向割边一定满流,反向割边流量一定为 \(0\)。如果正向割边残量不为 \(0\),那么就会形成一条增广路;如果反向割边流量不为 \(0\),那么根据反对称性,该边的反向边残量不为 \(0\),所以也会形成一条增广路。
割边相关
- 求出最小割上的边:跑完最大流后,在残量网络上根据割的定义求出 \(S\) 集合。如果 \(|S|+|T|\ne N\),则该图有多个最小割。
- 关键割边:增加该边容量会使最大流增大。\(u\in S\) 且 \(v\in T\)。
建模
-
割 <-> 离散的问题强制分成两类。
-
将代价转换为容量。消耗对应代价等价于切断该边。特别地,如果边权为 \(\infty\),表示这条边不能作为正向割边。
-
网格图上染色是常见模型(可以多色),进而让不合法的状态变成原点到汇点的一条路径,然后最优解即为最小割。
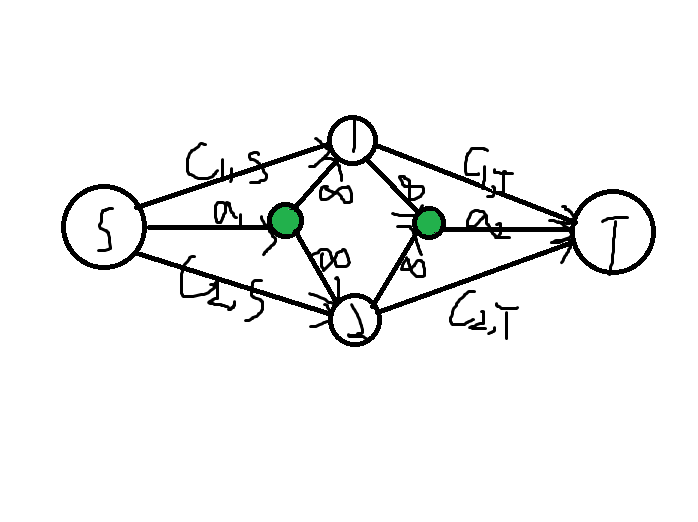
-
很有哲理的一张图\(^2\)。可以计算 \(1,2\) 在同一集合的额外贡献。容量为无穷使得最小割能自行抉择。
-
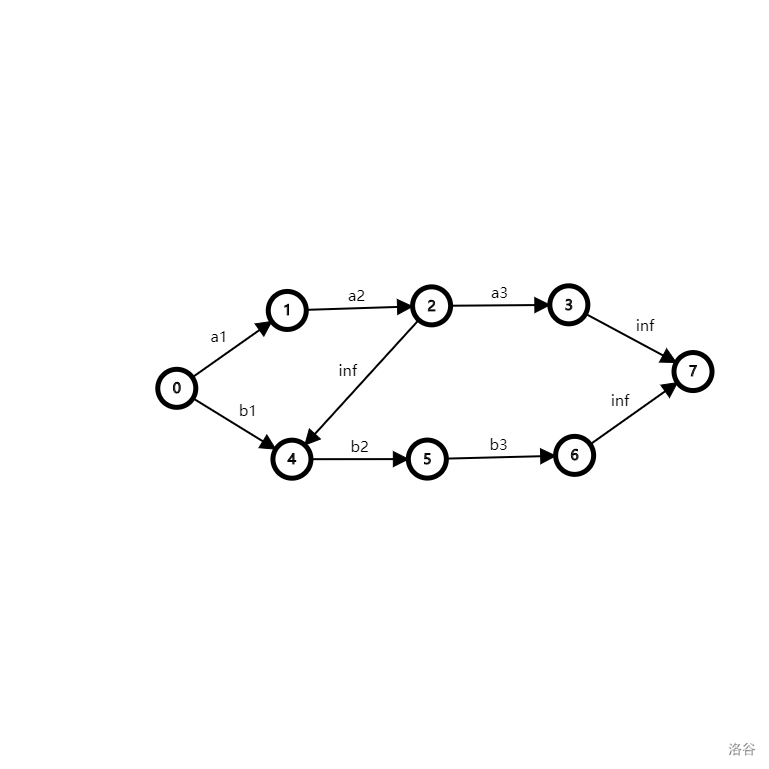
[HNOI2013] 切糕,用到上面类似的。如果没有 \(D\) 的限制,那么相当于有 \(P\times Q\) 条长为 \(R\) 的链,原点连向链头,链尾连向汇点,第 \(i\) 条边容量即为 \(v(P,Q,i)\) 。考虑加上 \(D\),如图
-
假如说 \(D=1\),发现如果 \((2,3)\) 这条边被割了,因为 \((2,4)\) 不能割,那么肯定不会去割 \((0,4)\),否则还需要割 \((4,5)\) 才能把图分成两个集合。
更一般的情况
考虑切糕模型,有 \(m\) 条链,每条链上有 \(n+1\) 个点,考虑映射到有 \(m\) 个数,每个数 \(\in[1,n]\)。然后 \((x_{i,j-1},x_{i,j},w(i,j))\) 就表示第 \(i\) 个数选择 \(j\) 的代价,为了避免第 \(i\) 个数取多个值,可以通过加入 \((x_{i,j},x_{i,j-1},\inf)\) 来实现。
然后考虑一条边 \((x_{a,i},x_{b,j},f(i,j))\) 表示什么,相当于就是说当第 \(a\) 个数 \(\ge i+1\),第 \(b\) 个数 \(\le j\) 时会有 \(f(i,j)\) 的代价,一般需要钦定 \(i\) 和 \(j\) 的大小关系,否则会算重。
假设 \(i\ge j\),现在我们需要的是当第 \(a\) 个数 \(=i+1\) 且第 \(b\) 个数 \(=j\) 的代价,假设我们要让它为 \(g(i,j)\),容易发现 \(g(i,j)=\displaystyle \sum_{j\le y\le x\le i}f(x,y)\)。然后就可以得到 \(f(i,i)=g(i,i)\),\(f(i,j)=g(i,j)-g(i-1,j)-g(i,j+1)+g(i-1,j+1)\)。
所以当 \(f(i,j)\ge 0\),即 \(g\) 满足四边形不等式就可以用这种建模。
最大权闭合子图
- 闭合子图(有向图):如果 \(\forall u\in S\),对于 \(u\) 的每一个出边 \((u,v)\),都有 \(v\in S\),则称 \(S\) 是一个闭合子图。
- 最大权闭合子图:对于 \(u\) 有点权 \(a_u\),满足 \(\sum\limits_{u\in S}a_u\) 最大的 \(S\) 称为最大权闭合子图。
定理
构图:原点 \(s\) 向 \(a_u>0\) 的 \(u\) 连容量为 \(a_u\) 的边,\(a_u<0\) 的 \(u\) 向汇点 \(t\) 连容量为 \(-a_u\) 的边,原图上如果存在 \((u,v)\),那么在 \(u,v\) 之间连边权为 \(\inf\) 的边。
定理:最大权 \(=\) 所有正点权之和 \(-\) 最小割。
证明:对于原图上的边,因为容量为 \(\inf\),所以不能被割掉。对于 \((s,u)\),割掉意味着不选这个点,因为 \(a_u>0\),所以尽量让和最小;对于 \((u,t)\),割掉意味着选这个点,因为 \(a_u<0\),所以尽量让 \(-a_u\) 和最小。发现这是最小割,证毕。
全局最小割 Stoer-Wagner
Minimum Steiner Cut。
\(O(\log^3 n)\) 次最大流。
费用流
流程
最大流的基础上,每条边多了一个费用 \(c(u,v)\)。要求最大流的前提下费用最小。类似于反对称性,有 \(c(v,u)=-c(u,v)\)。
于是有贪心做法,每次选费用最小的增广路进行增广。新增的代价为 \(\sum c\times \min g\)。
EK+SPFA 即可。
例题&建模
直接考虑第二问,发现只需要在残量网络上,对于原有的边 \((u,v)\) 新增一条容量 \(\inf\) 费用 \(w(u,v)\) 的边,然后进入 \(s\) 的流量为 \(k\) 即可。
令盘子为餐巾。
因为每天有脏盘子和新盘子两种情况,所以拆成两个点 \(i\) 和 \(i'\)。\(s\) 向 \(i\) 连 \((r_i,0)\) 的边(分别表示容量和费用),表示经过第 \(i\) 天会得到 \(r_i\) 个脏盘子。\(s\) 向 \(i'\) 连 \((r_i,p)\) 的边,表示买新盘子。\(i'\) 向 \(t\) 连 \((r_i,0)\) 的边,表示第 \(i\) 天需要 \(r_i\) 个新盘子。
由于每天的脏盘子可以继承,所以 \(i\) 向 \(i+1\) 连 \((\inf,0)\) 的边。考虑快洗,即 \(i\) 向 \((i+m)'\) 连 \((\inf,f)\) 的边,表示第 \(i+m\) 天得到这么多新盘子。慢洗同理。
拆边加拆点。
考虑黑白染色。因为考虑转弯与直行,所以将每个点 \(x\) 拆成两个点 \(x_1\) 和 \(x_2\) 分别表示水平和竖直。
\(s\) 向黑点 \(b\) 连 \((2,0)\),表示 \(b\) 需要和其他两个点连边。白点 \(w\) 向 \(t\) 连 \((2,0)\),同理。\(b\) 向 \(b_1\) 和 \(b_2\) 分别连容量为 \(2\) 的边,\(w_1\) 和 \(w_2\) 分别向 \(w\) 连容量为 \(2\) 的边,表示进行选择。然后只需要对于上下两个点,竖直与竖直相连,对于左右两个点,水平与水平相连。
考虑加上权值,发现当流入 \(b\) 的流量 \(2\) 向 \(b_1\) 和 \(b_2\) 都有流量的时候才能加上权值,于是考虑拆边。把容量为 \(2\) 的边拆成 \((1,\frac{s}{2})\) 和 \((1,-\frac{s}{2})\) 的边,然后 \(w\) 同理。于是跑最大费用流即可。
以下问题均用到了链式构图。类似于切糕的构图,但是每个点都在一条链上。
考虑如下构图:
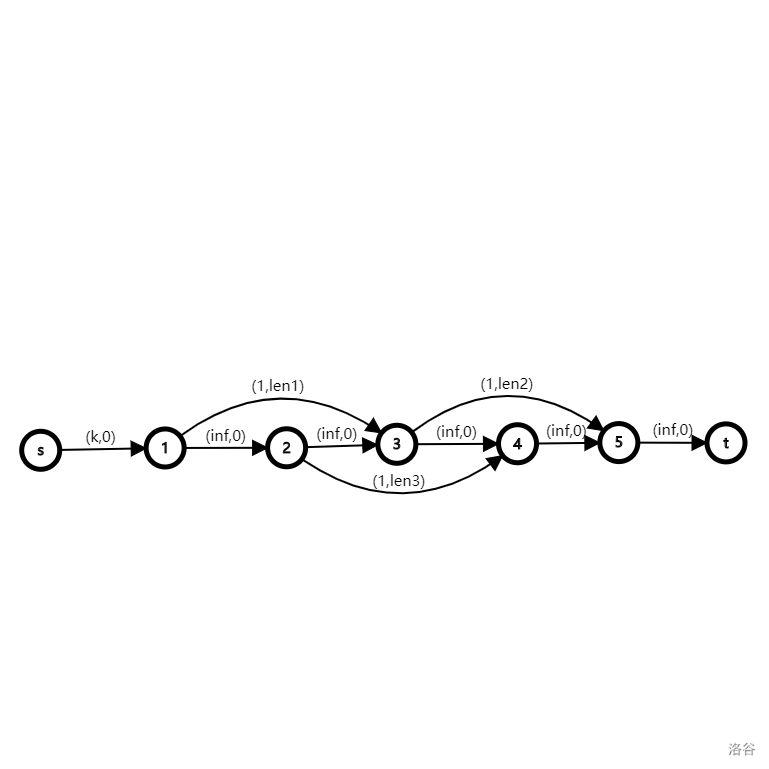
其中 \(1\sim 5\) 就对应所有区间内的点,\((1,3)\) 表示区间 \([1,3)\)。容易发现,原问题等价于在该图上选 \(k\) 条路径,每条路径由若干不相交的区间构成。于是可得到该图。
同理采用以上构图。先给出构图:
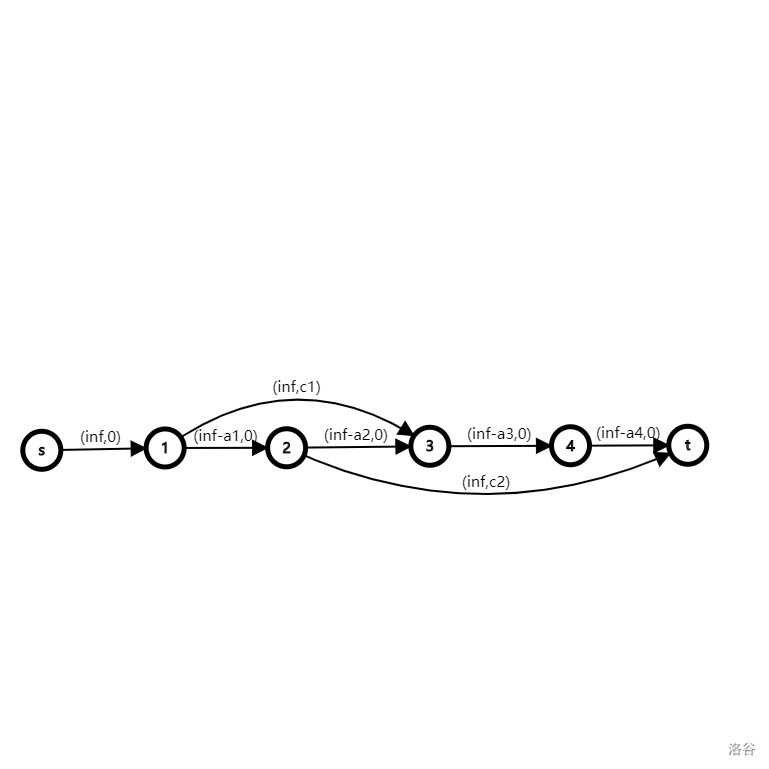
第 \(i\) 个点表示第 \(i\) 天。为了实现至少 \(a_i\) 个志愿者,将 \((i,i+1)\) 的容量设为 \(\inf -a_i\)。发现该图的最大流为 \(\inf\) 而由于这条边最多只能通过 \(\inf -a_i\) 的流量,所以跨过该边的流量即在当天志愿者的数量需要 \(\ge a_i\)。于是得到该图。
二维平面上有 \(n\) 个白点和 \(n\) 个黑点,每个白点 \((wx_i,wy_i)\) 上有 \(wc_i\) 个白球,黑球同理。如果将白球 \((wx,wy)\) 与黑球 \((bx,by)\) 匹配,则贡献是 \(|wx-bx|+|wy-by|\)。保证黑球的数量等于白球的数量,求最大权完美匹配,\(n\le 10^3\)。
有一个最基本的思路,每个黑点与白点间都连一条相应代价的边,但这样边数是 \(O(n^2)\),显然无法通过。
考虑优化。主要问题在于绝对值,发现 \(|wx-bx|+|wy-by|\) 只有四种情况,于是建四个虚点分别表示每种情况。由于跑最大费用最大流,所以即使走不合法的路径也一定不优。
模拟费用流
不建图,用数据结构来模拟费用流执行的过程,即模拟费用流。
本质是,用数据结构来处理“反悔”操作,即费用流里面的“退流”。
上下界网络流
特殊情况
整体限制 \([l,r]\)。考虑把所有容量都减去 \(l\)。
其他
无源汇上下界可行流。
给每条边预分配 \(l_i\) 的流量,然后将边的容量改为 \(r_i-l_i\),这样得到的图可能不满足流量守恒,所以需要新开超级源点 \(S\) 向入流量多的连边,出流量多的向 \(T\) 连边,在该图上跑最大流如果满足 \(S\) 连出的边满流就一定可行。
有源汇上下界可行流。
对于 \(s\) 和 \(t\) 不需要流量守恒,所以增加 \((t,s,0,\infty)\) 变成无源汇问题,此时 \(s\to t\) 的流量为这条边的流量。
有源汇上下界最大/小流。
先求出一个可行流,然后在 \((t,s,0,\infty)\) 删掉后的残量网络上跑最大流,两次流量之和即为答案,因为最大流可以反悔。
最小流即为可行流减去 \(t\to s\) 的最大流。
注:
\(^1\):如果一个点贪污,即出流量小于入流量,那么它就可以处十年以上有期徒刑或者无期徒刑,并处罚金或者没收财产;数额特别巨大,并使国家和人民利益遭受特别重大损失的,处无期徒刑或者死刑,并处没收财产。
\(^2\):出自 Just_int_mian 网络流建模合集。
特别鸣谢:
@wxr_,多次为本文做出贡献,包括但不仅限于校正。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号