Codeforces Round #721 (Div. 2) [未完待续]

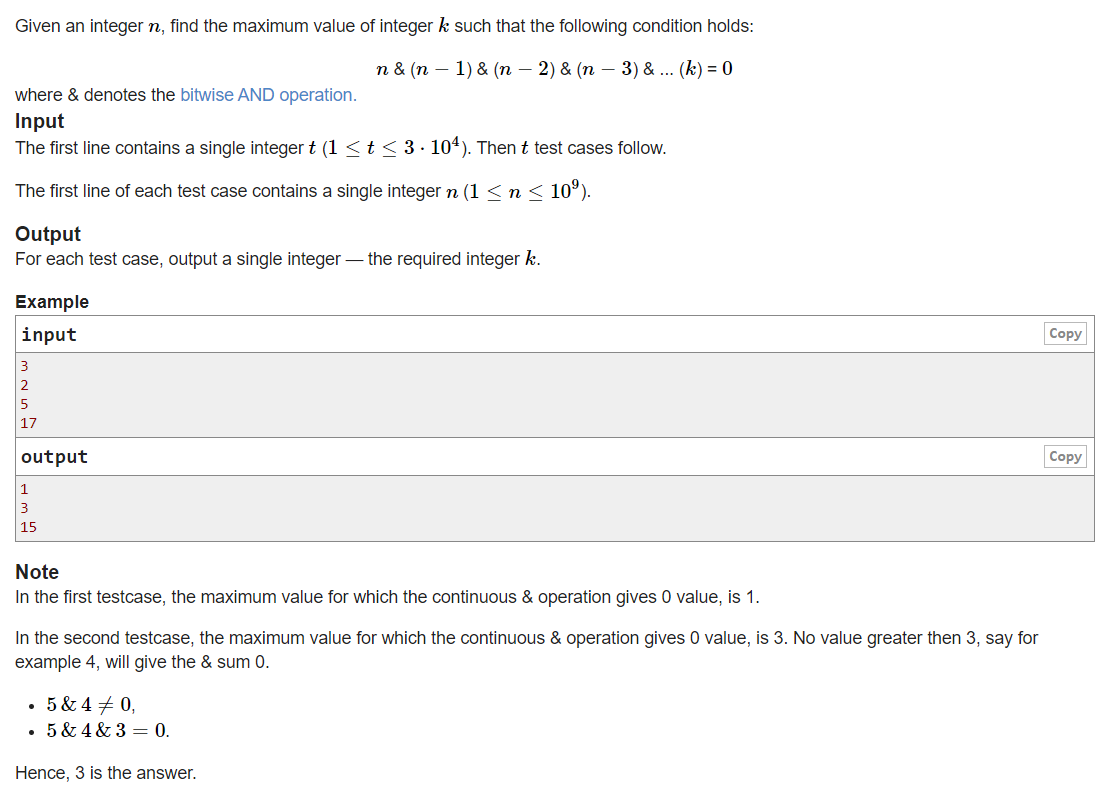
A. And Then There Were K

题目描述

参考题解

#include <bits/stdc++.h>
using namespace std;

void solve(){
    int n;
    cin >> n;
    int a = 1;
    while(a * 2 <= n) a *= 2;
    cout << (a - 1) << '\n';
}

int main(){
    int T;
    cin >> T;
    while(T--) solve();
}

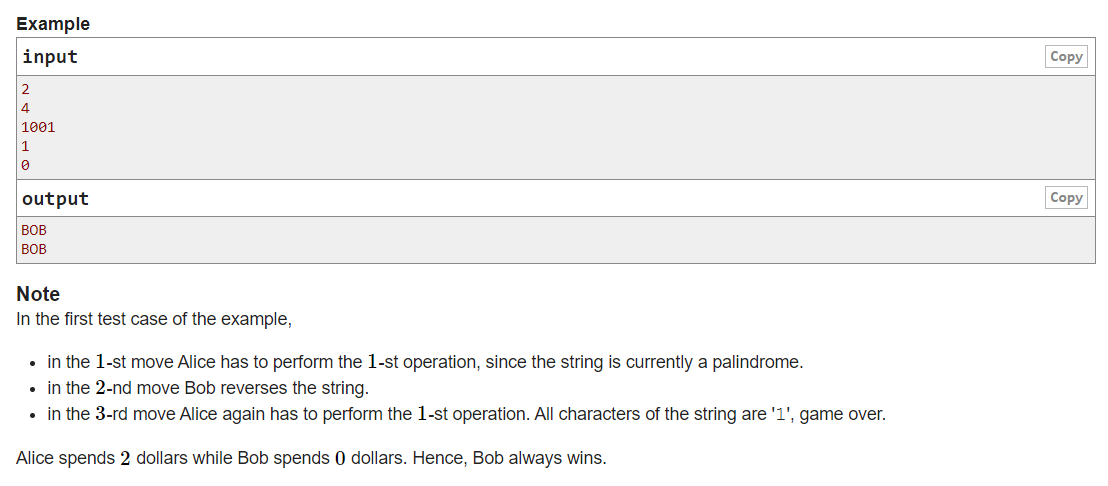
B1. Palindrome Game (easy version)

题目描述

参考题解

博弈论

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <deque>
#include <string>
#include <unordered_map>

using namespace std;

const int INF = 0x3f3f3f3f, N = 1e5+5;

typedef long long LL;

int n;

int main()
{
    int T;
    cin >> T;
    while(T --)
    {
        scanf("%d", &n);
        string s;
        cin >> s;
        int cnt1 = 0; //cnt1: 对称0数
        for(int i = 0; i < n; ++ i)
        {
            if(s[i] == '0')
            {
                if(s[i] == s[n-1-i])
                {
                    cnt1 ++;
                }
            }
        }
        if(cnt1 == 1 || cnt1%2 == 0)
        {
            printf("BOB\n");
        }
        else
        {
            printf("ALICE\n");
        }
    }
    return 0;
}

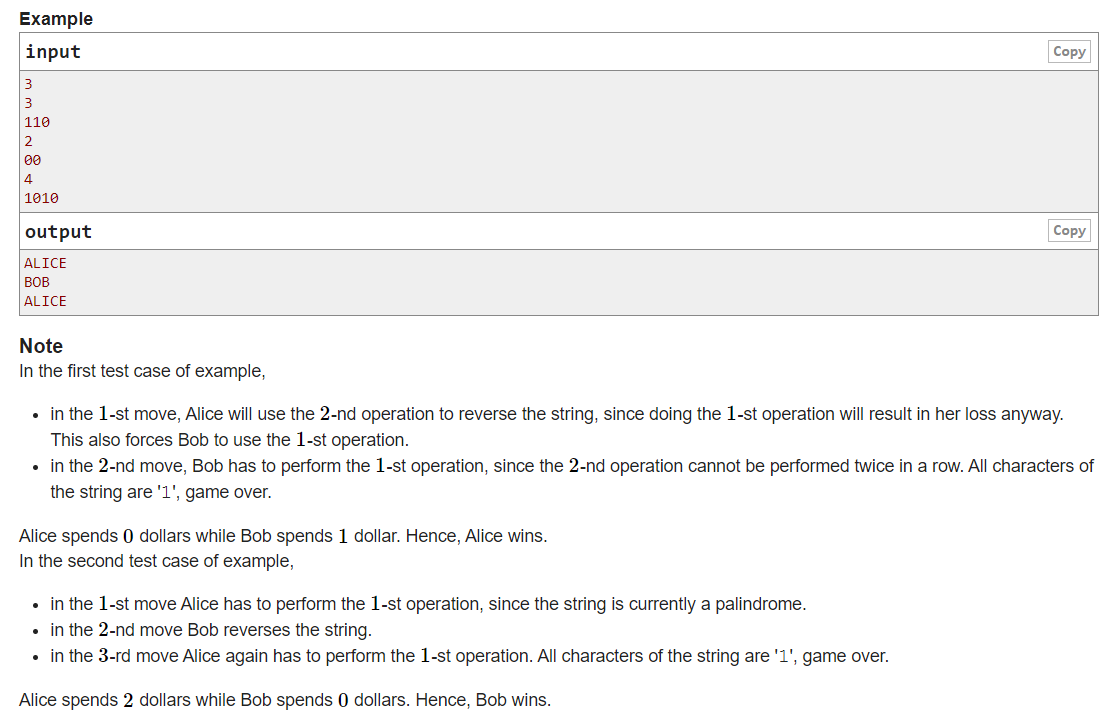
B2. Palindrome Game (hard version)

题目描述

参考题解

博弈论，很难

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <deque>
#include <string>
#include <unordered_map>

using namespace std;

const int INF = 0x3f3f3f3f, N = 1e5+5;

typedef long long LL;

int n;

int main()
{
    int T;
    cin >> T;
    while(T --)
    {
        scanf("%d", &n);
        string s;
        cin >> s;
        int cnt1 = 0, cnt2 = 0; //cnt1: 对称0数， cnt2: 非对称0数
        for(int i = 0; i < n; ++ i)
        {
            if(s[i] == '0')
            {
                if(s[i] == s[n-1-i])
                {
                    cnt1 ++;
                }
                else
                {
                    cnt2 ++;
                }
            }
        }
        if(cnt2 == 0)
        {
            if(cnt1 == 1 || cnt1%2 == 0)
            {
                printf("BOB\n");
            }
            else
            {
                printf("ALICE\n");
            }
        }
        else
        {
            if(cnt1 == 1)
            {
                if(cnt2 == 1)
                {
                    printf("DRAW\n");
                }
                else
                {
                    printf("ALICE\n");
                }
            }
            else
            {
                printf("ALICE\n");
            }
        }
    }
    return 0;
}

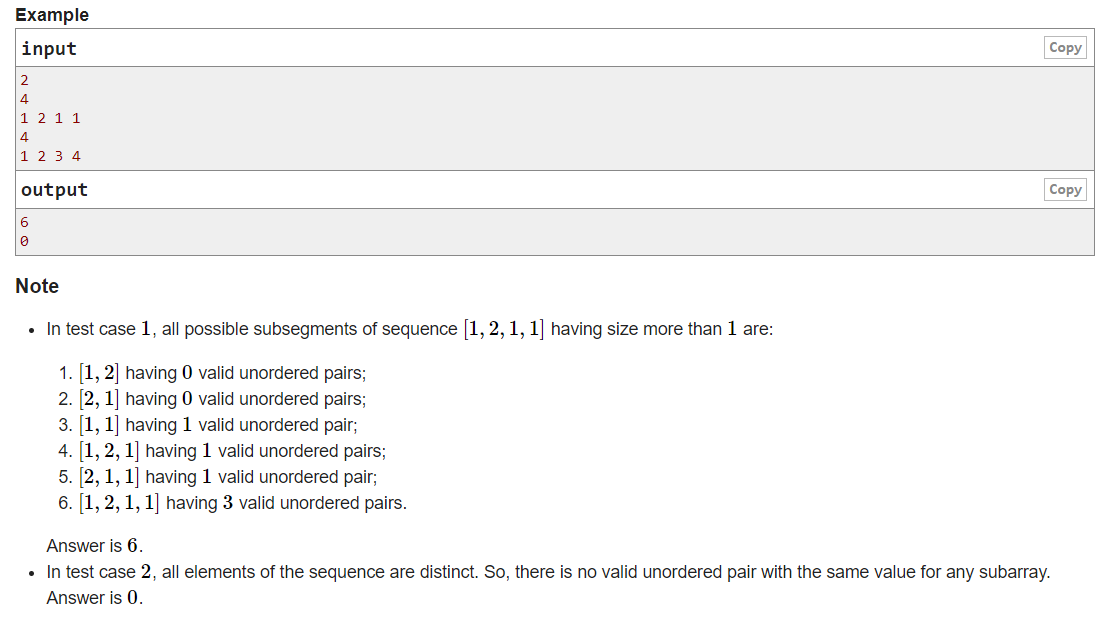
C. Sequence Pair Weight

题目描述

参考题解

感谢ccsu_madoka分享的题解
题意：给一个数组，求他的所有连续子串中，任取相等的两数的方案之和。
题解：这个题其实，造个全是1的数组乱搞算出来就差不多了。
当计算i的贡献时，我们计算前面所有a[i]的贡献，同时对于每一个包含i的后缀都可以算一次i前面的贡献，所以ans加上map[a[i]]*(n-i+1);
当a[i]在第i个位置时，可为后面的数贡献i个子串，所以每次算完贡献后我们在map[a[i]]中加 i

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <deque>
#include <string>
#include <unordered_map>

using namespace std;

const int INF = 0x3f3f3f3f, N = 1e5+5;

typedef long long LL;

int n;

LL a[N];

unordered_map<int, LL> ma;


int main()
{
    int T;
    cin >> T;
    while(T --) {
        ma.clear();
        scanf("%d", &n);
        for (int i = 0; i < n; ++i)
        {
            scanf("%d", a+i);
        }
        LL ans = 0;
        for(int i = 0; i < n; ++ i)
        {
            if(ma.count(a[i]))
            {
                ans += ma[a[i]] * (n-1-i+1);
            }
            ma[a[i]] += (i+1);
        }
        printf("%lld\n", ans);
    }
    return 0;
}