组合计数

第一类Stirling数

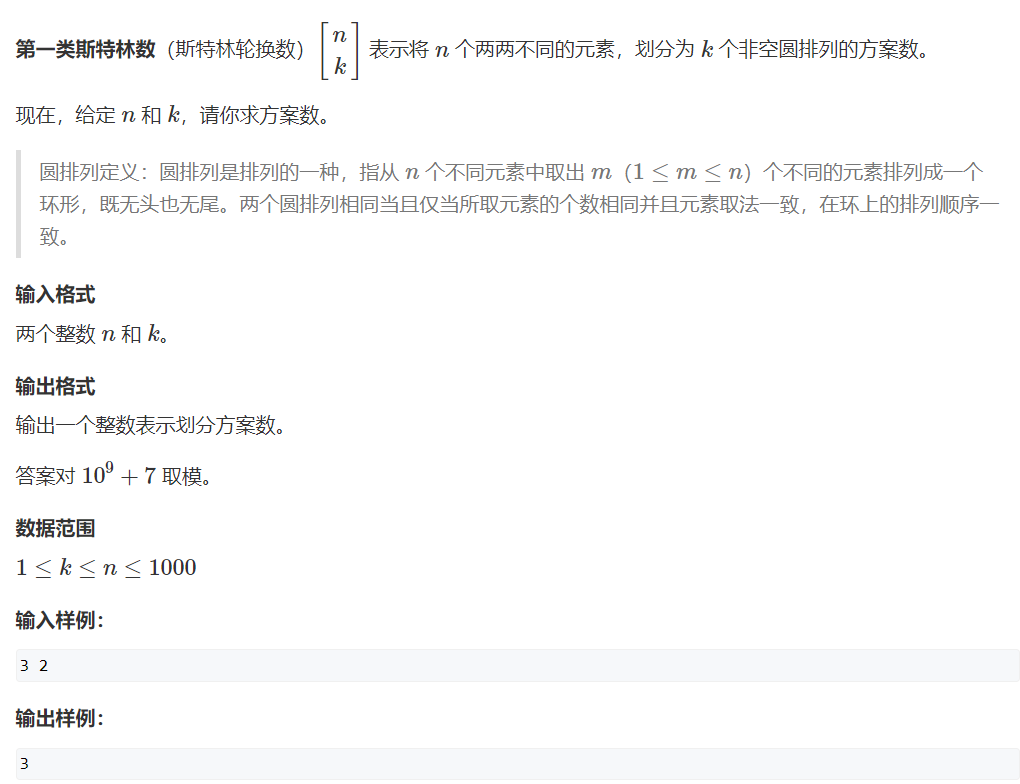
第一类斯特林数

题目描述

参考题解

Stirling数模板题

#include <iostream>
#include <cstdio>

using namespace std;

const int N = 1e3+5, MOD = 1e9+7;

typedef long long LL;

int n, k;

int dp[N][N]; //dp[i][j]: 从i个物中选出j个圆排列的方案数

int main()
{
    cin >> n >> k;
    dp[0][0] = 1;
    for(int  i = 1; i <= n; ++ i)
        for(int j = 1; j <= k; ++ j) //dp[i][>i] = 0;
        {
            dp[i][j] = (dp[i-1][j-1] + (i-1)*(LL)dp[i-1][j]%MOD)%MOD;
        }
    cout << dp[n][k] << endl;
    return 0;
}

恰有 K 根木棍可以看到的排列数目

题目描述

参考题解

dp[i][j],第一类斯特林数：从i个数中分出j个圆排列的方案数

#include <iostream>
#include <cstdio>

using namespace std;

const int N = 5e3+5, INF = 0x3f3f3f3f, MOD = 1e9+7;

typedef long long LL;

int dp[N][N]; //dp[i][j],第一类斯特林数：从i个数中分出j个圆排列的方案数

class Solution {
public:
    int rearrangeSticks(int n, int k) {
        dp[0][0] = 1;
        for(int i = 1; i <= n; ++ i)
            for(int j = 1; j <= k; ++ j)
            {
                dp[i][j] = (dp[i-1][j-1] + (i-1)*(LL)dp[i-1][j]%MOD)%MOD;
            }
        return dp[n][k];
    }
};

第二类Stirling数

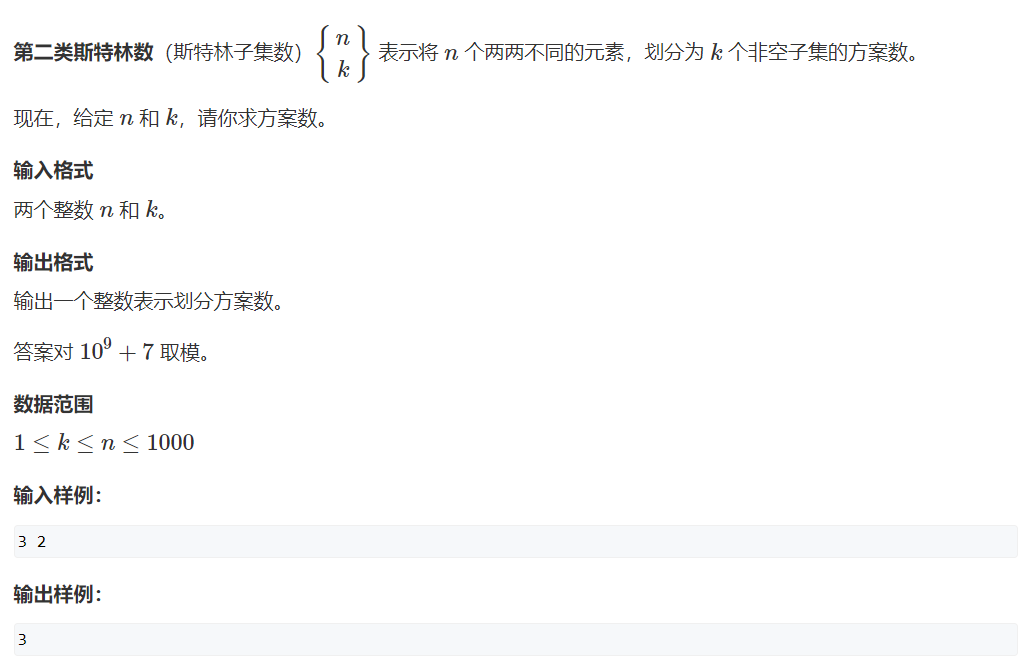
第二类斯特林数

题目描述

参考题解

//dp[i][j]表示第二类stirling数，i个不同的数分成j给非空子集的方案数

#include <iostream>
#include <cstdio>

using namespace std;

const int N = 1e3+5, MOD = 1e9+7;

typedef long long LL;

int n, k;

int dp[N][N]; //dp[i][j]表示第二类stirling数，i个不同的数分成j给非空子集的方案数

int main()
{
    cin >> n >> k;
    dp[0][0] = 1;
    for(int i = 1; i <= n; ++ i)
        for(int j = 1; j <= k; ++ j)
        {
            dp[i][j] = (dp[i-1][j-1] + j*(LL)dp[i-1][j]%MOD)%MOD;
        }
    cout << dp[n][k] << endl;
    return 0;
}