线段树

单点修改 + 区间最大值

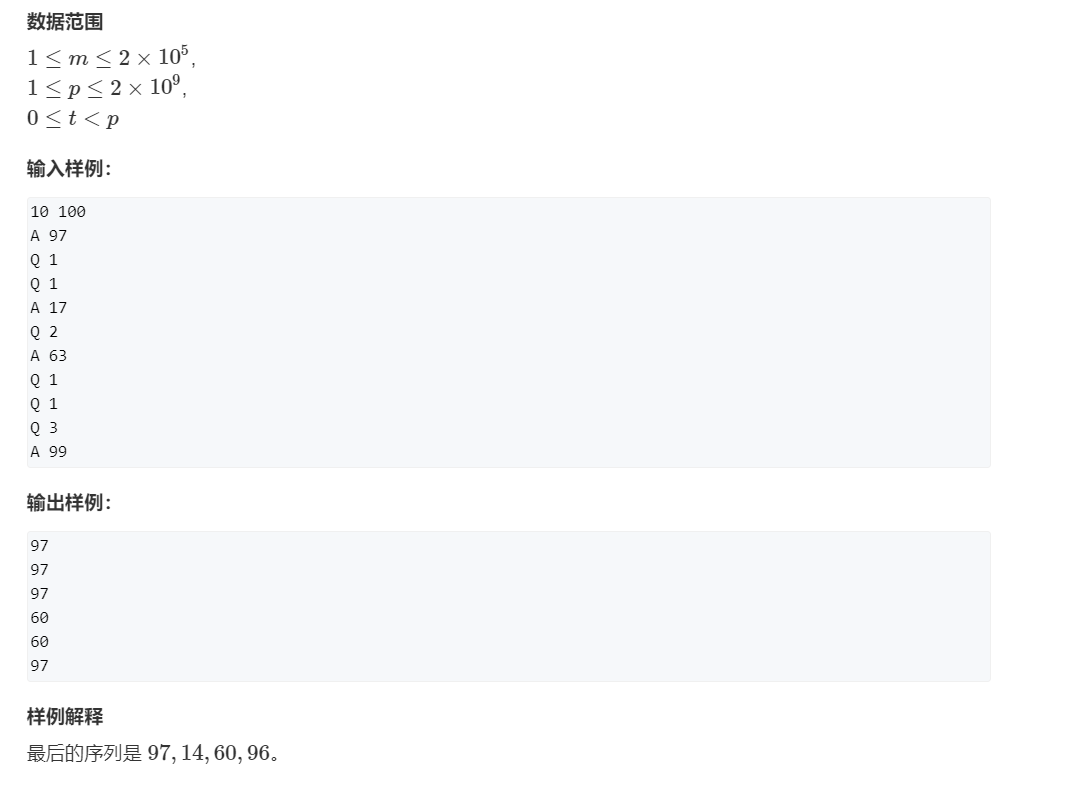
最大数

题目描述

参考题解

#include <iostream>
#include <cstdio>

using namespace std;

const int N = 2e5+5, INF = 0x3f3f3f3f;

int m, p;

struct Node{
    int l ,r;
    int v;
}tree[N*4];

//在非叶子节点执行
void pushup(int u)
{
    tree[u].v = max(tree[u<<1].v, tree[u<<1|1].v);
}

void build(int u, int l, int r)
{
    tree[u] = {l, r, 0};
    if(l == r)  return;
    int mid = l+r>>1;
    build(u<<1, l, mid);
    build(u<<1|1, mid+1, r);
    pushup(u);
}

//区间查询
int query(int u, int l, int r)
{
    //完全包含
    if(tree[u].l >= l && tree[u].r <= r)
    {
        return tree[u].v;
    }
    //不会出现交集为空的情况
    //有交集,需要思考清楚
    int mid = tree[u].l + tree[u].r >> 1;
    int v1 = -INF, v2 = -INF; //这里初始化要谨慎
    if(mid >= l) //左边与区间有交集
    {
        v1 = query(u<<1, l, r);
    }
    if(mid+1 <= r) //右边与区间有交集
    {
        v2 = query(u<<1|1, l, r);
    }
    return max(v1, v2);
}

//单点修改
void modify(int u, int x, int v)
{
    if(tree[u].l == tree[u].r)
    {
        tree[u].v = v;
        return ;
    }
    int mid = tree[u].l + tree[u].r >> 1;
    if(x <= mid) //在左边
    {
        modify(u<<1, x, v);
    }
    else //在右边
    {
        modify(u<<1|1, x, v);
    }
    pushup(u);
}


int n = 0; //总数

int main()
{
    cin >> m >> p;
    build(1, 1, m);
    int last = 0;
    for(int i = 0; i < m; ++ i)
    {
        char op[2];
        int t;
        scanf("%s%d", op, &t);
        if(op[0] == 'Q')
        {
            last = query(1, n-t+1, n);
            cout << last << endl;
        }
        else
        {
            modify(1, ++n, (t+last)%p);
        }
    }
    return 0;
}

单点修改 + 最大连续子段和

你能回答这些问题吗

题目描述

参考题解

#include <iostream>
#include <cstdio>
#include <algorithm>

using namespace std;

const int N = 5e5+5;

int n, m;

struct Node{
    int l, r;
    int tsum;
    int lsum, rsum;
    int sum;
}tree[N*4];

void pushup(Node &node, Node &lnode, Node &rnode)
{
    node.sum = lnode.sum + rnode.sum;
    node.lsum = max(lnode.lsum, lnode.sum + rnode.lsum);
    node.rsum = max(rnode.rsum, rnode.sum + lnode.rsum);
    node.tsum = max(max(lnode.tsum, rnode.tsum), lnode.rsum + rnode.lsum);
}

void pushup(int u)
{
    pushup(tree[u], tree[u<<1], tree[u<<1|1]);
}

void build(int u, int l, int r)
{
    tree[u] = {l, r, 0, 0, 0, 0};
    if(l == r)
    {
        return;
    }
    int mid = l+r>>1;
    build(u<<1, l, mid);
    build(u<<1|1, mid+1, r);
    pushup(u);
}

//将第x个数改为v
void modify(int u, int x, int v)
{
    if(tree[u].l == tree[u].r)
    {
        tree[u] = {tree[u].l, tree[u].r, v, v, v, v}; //lsum, rsum必须有元素
        return;
    }
    int mid = tree[u].l + tree[u].r >> 1;
    if(x <= mid)
    {
        modify(u<<1, x, v);
    }
    else
    {
        modify(u<<1|1, x, v);
    }
    pushup(u);
}

//查询区间L~R的最大连续子段和
Node query(int u, int L, int R)
{
    if(tree[u].l >= L && tree[u].r <= R)
    {
        return tree[u];
    }
    int mid = tree[u].l + tree[u].r >> 1;
    Node ltree, rtree;
    bool haveL = false, haveR = false;
    if(mid >= L) //包含左子树
    {
        ltree = query(u<<1, L, R);
        haveL = true;
    }
    if(mid+1 <= R) //包含右子树
    {
        rtree = query(u<<1|1, L, R);
        haveR = true;
    }
    if(haveL && haveR)
    {
        Node ans;
        pushup(ans, ltree, rtree);
        return ans;
    }
    else if(haveL)
    {
        return ltree;
    }
    else if(haveR)
    {
        return rtree;
    }

}

int main()
{
    cin >> n >> m;
    build(1, 1, n);
    for(int i = 1; i <= n; ++ i)
    {
        int tp;
        scanf("%d", &tp);
        modify(1, i, tp);
    }
    while(m --)
    {
        int k, x, y;
        scanf("%d%d%d", &k, &x, &y);
        if(k == 1)
        {
            if(x > y)   swap(x, y);
            Node ans = query(1, x, y);
            printf("%d\n", ans.tsum);
        }
        else
        {
            modify(1, x, y);
        }
    }
    return 0;
}

区间修改 + 区间最大公约数

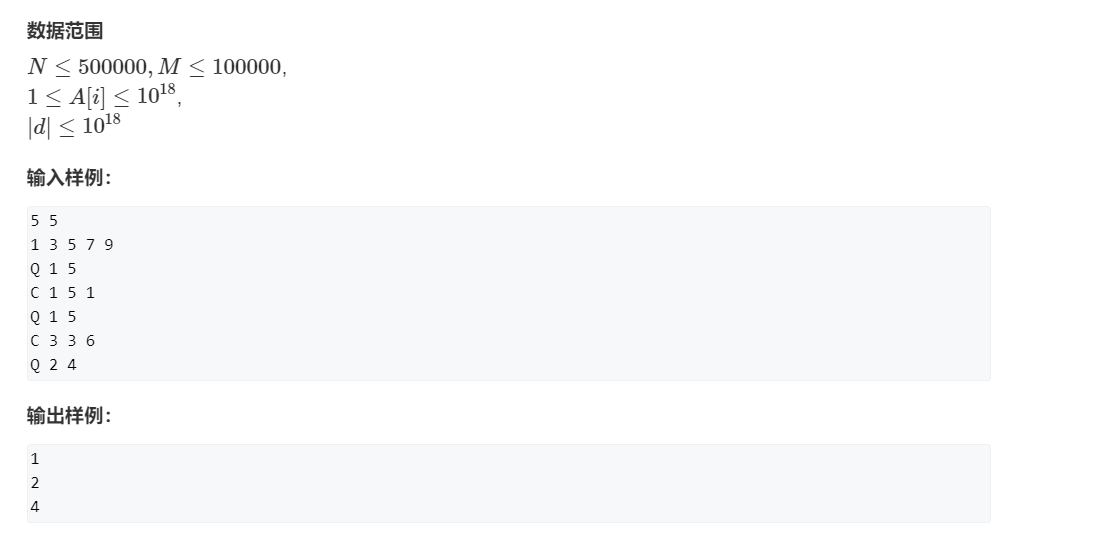
区间最大公约数

题目描述

参考题解

利用差分转单点修改

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>

using namespace std;

const int N = 5e5+5;

typedef long long LL;

int n, m;
LL w[N]; //存差分数组
LL gcd(LL a, LL b)
{
    return b? gcd(b, a%b) : a;
}

//线段树作用：求区间和，求区间gcd
struct Node{
    int l, r;
    LL sum; //区间和
    LL v; //区间最大公因数
}tree[N*4];

void pushup(Node &treeu, Node &treel, Node &treer)
{
    treeu.v = abs(gcd(treel.v, treer.v));
    treeu.sum = treel.sum + treer.sum;
}

void pushup(int u)
{
    pushup(tree[u], tree[u<<1], tree[u<<1|1]);
}

void build(int u, int l, int r)
{
    tree[u] = {l, r, 0, 1};
    if(l == r)
    {
        return;
    }
    int mid = l+r>>1;
    build(u<<1, l, mid);
    build(u<<1|1, mid+1, r);
    pushup(u);
}

void modify(int u, int x, LL v)
{
    if(tree[u].l == tree[u].r)
    {
        tree[u].sum = v;
        tree[u].v = v;
        return;
    }
    int mid = tree[u].l + tree[u].r >> 1;
    if(x <= mid)
    {
        modify(u<<1, x, v);
    }
    else
    {
        modify(u<<1|1, x, v);
    }
    pushup(u);
}

//返回区间和，与区间gcd
Node query(int u, int L, int R)
{
    //完全包含
    if(L <= tree[u].l && tree[u].r <= R)
    {
        return tree[u];
    }
    int mid = tree[u].l + tree[u].r >> 1;
    Node treel, treer;
    if(mid >= L && mid+1 <= R) //既包含左子树又包含右子树
    {
        Node treeu;
        treel = query(u<<1, L, R);
        treer = query(u<<1|1, L, R);
        //计算要返回的信息
        pushup(treeu, treel, treer);
        return treeu;
    }
    else //只包含一方
    {
        if(mid >= L) //包含左子树
        {
            return query(u<<1, L, R);
        }
        if(mid+1 <= R) //包含右子树
        {
            return query(u<<1|1, L, R);
        }
    }
}

int main()
{
    cin >> n >> m;
    build(1, 1, n);
    memset(w, 0, sizeof w);
    for(int i = 1; i <= n; ++ i)
    {
        LL tp;
        scanf("%lld", &tp);
        w[i] += tp;
        w[i+1] -= tp;
        modify(1, i, w[i]);
    }
    while(m --)
    {
        char op[2];
        int l, r;
        scanf("%s%d%d", op, &l, &r);
        if(op[0] == 'C')
        {
            LL d;
            scanf("%lld", &d);
            w[l] += d;
            modify(1, l, w[l]);
            if(r+1<=n)
            {
                w[r+1] -= d;
                modify(1, r+1, w[r+1]);
            }
        }
        else
        {
            LL vl = query(1, 1, l).sum;
            LL vgcd = vl;
            if(l+1<=r)
            {
                vgcd = query(1, l+1, r).v;
            }
            LL ans = abs(gcd(vl, vgcd));
            printf("%lld\n", ans);
        }
    }
    return 0;
}

区间修改 + 查询区间和

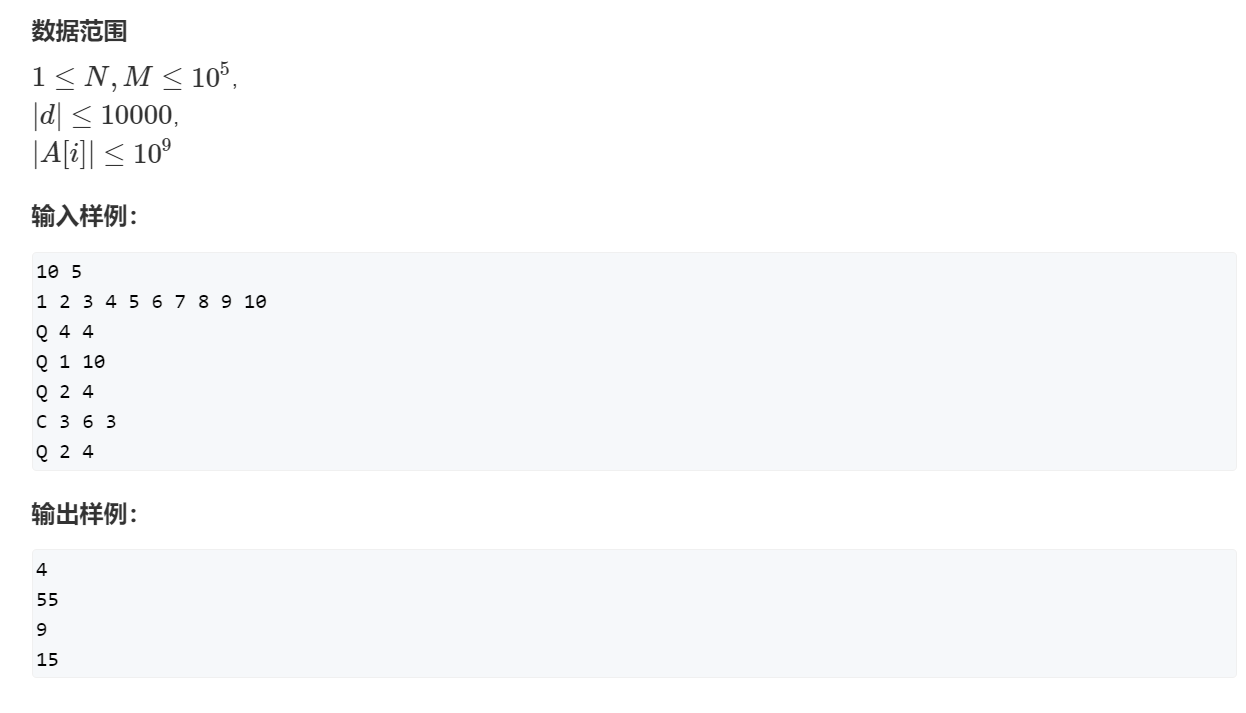
一个简单的整数问题2

题目描述

参考题解

#include <iostream>
#include <cstdio>

using namespace std;

const int N = 1e5+5;

typedef long long LL;

struct Node{
    int l, r;
    LL sum;
    int add; //所有lazy标记记录的状态不包括当前节点
}tree[N*4];

void pushup(int u)
{
    tree[u].sum = tree[u<<1].sum + tree[u<<1|1].sum;
}

void pushdown(int u)
{
    Node &tl = tree[u<<1], &tr = tree[u<<1|1], &t = tree[u];
    tl.sum += (tl.r-tl.l+1)*(LL)t.add;
    tl.add += t.add;
    tr.sum += (tr.r-tr.l+1)*(LL)t.add;
    tr.add += t.add;
    t.add = 0;
}

void build(int u, int l, int r)
{
    tree[u] = {l, r, 0, 0};
    if(l == r)
    {
        return ;
    }
    int mid = l+r>>1;
    build(u<<1, l, mid);
    build(u<<1|1, mid+1, r);
    pushup(u);
}

void modify(int u, int L, int R, int v)
{
    if(L <= tree[u].l && tree[u].r <= R)
    {
        tree[u].sum += (tree[u].r - tree[u].l + 1)*(LL)v; //注意这里
        tree[u].add += v;
        return;
    }
    pushdown(u);
    int mid = tree[u].l+tree[u].r>>1;
    if(mid >= L)
    {
        modify(u<<1, L, R, v);
    }
    if(mid+1 <= R)
    {
        modify(u<<1|1, L, R, v);
    }
    pushup(u);
}

LL query(int u, int L, int R)
{
    if(L <= tree[u].l && tree[u].r <= R)
    {
        return tree[u].sum;
    }
    pushdown(u);
    int mid = tree[u].l+tree[u].r>>1;
    LL sum = 0;
    if(mid >= L)
    {
        sum += query(u<<1, L, R);
    }
    if(mid+1 <= R)
    {
        sum += query(u<<1|1, L, R);
    }
    return sum;
}

int n, m;

int main()
{
    cin >> n >> m;
    build(1, 1, n);
    for(int i = 1; i <= n; ++ i)
    {
        int tp;
        scanf("%d", &tp);
        modify(1, i, i, tp);
    }
    while(m --)
    {
        char op[2];
        int l, r;
        scanf("%s%d%d", op, &l, &r);
        if(op[0] == 'C')
        {
            int d;
            scanf("%d", &d);
            modify(1, l, r, d);
        }
        else
        {
            printf("%lld\n", query(1, l, r));
        }
    }
    return 0;
}

区间修改(带乘法) + 查询区间和

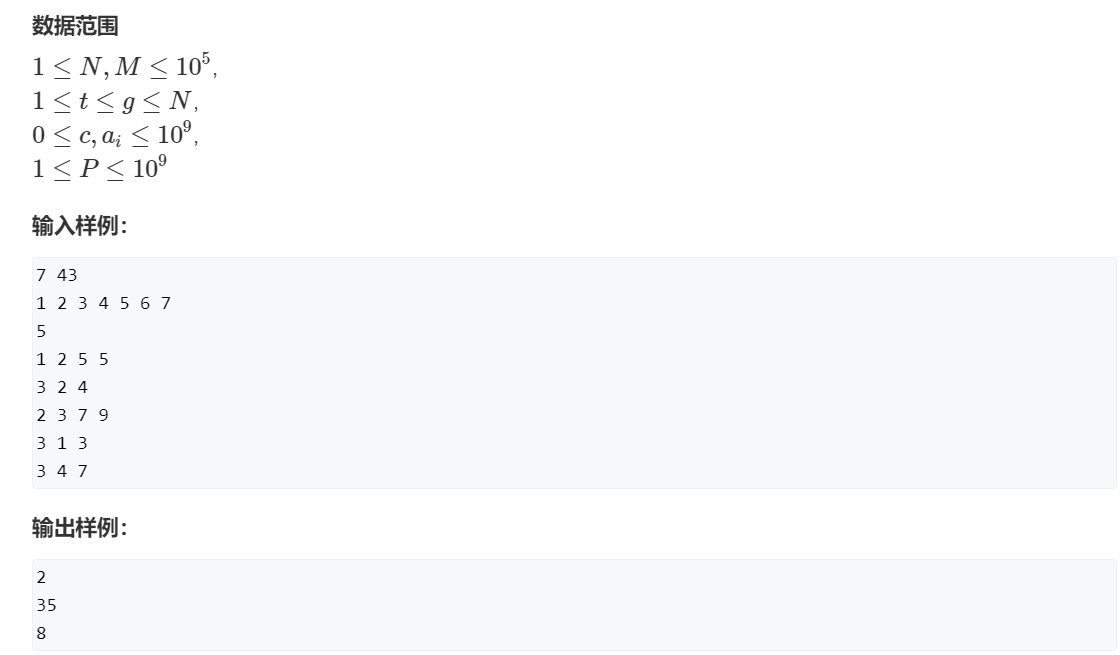
维护序列

题目描述

参考题解

#include <iostream>
#include <cstdio>

using namespace std;

const int N = 1e5+5;

typedef long long LL;

struct Node{
    int l, r;
    int sum;
    int add; //所有lazy标记记录的状态不包括当前节点
    int mul;
}tree[N*4];

int n, mod;

void pushup(int u)
{
    tree[u].sum = (tree[u<<1].sum + tree[u<<1|1].sum)%mod;
}

void eavl(Node &t, int addv, int mulv)
{
    //先乘后加
    t.sum = (t.sum*(LL)mulv + (t.r-t.l+1)*(LL)addv)%mod;
    t.mul = t.mul*(LL)mulv%mod;
    t.add = (t.add*(LL)mulv+addv)%mod;
}

void pushdown(int u)
{
    eavl(tree[u<<1], tree[u].add, tree[u].mul);
    eavl(tree[u<<1|1], tree[u].add, tree[u].mul);
    tree[u].add = 0;
    tree[u].mul = 1;
}


void build(int u, int l, int r)
{
    tree[u] = {l, r, 0, 0, 1};
    if(l == r)
    {
        return ;
    }
    int mid = l+r>>1;
    build(u<<1, l, mid);
    build(u<<1|1, mid+1, r);
    pushup(u);
}

void modify(int u, int L, int R, int addv, int mulv)
{
    if(L <= tree[u].l && tree[u].r <= R)
    {
        //更新当前节点: 先乘后加
        eavl(tree[u], addv, mulv);
        return;
    }
    //需要分裂节点
    pushdown(u); //注意
    int mid = tree[u].l+tree[u].r>>1;
    if(mid >= L)
    {
        modify(u<<1, L, R, addv, mulv);
    }
    if(mid+1 <= R)
    {
        modify(u<<1|1, L, R, addv, mulv);
    }
    pushup(u);
}

int query(int u, int L, int R)
{
    if(L <= tree[u].l && tree[u].r <= R)
    {
        return tree[u].sum;
    }
    pushdown(u); //注意
    int mid = tree[u].l+tree[u].r>>1;
    int sum = 0;
    if(mid >= L)
    {
        sum += query(u<<1, L, R);
        sum %= mod;
    }
    if(mid+1 <= R)
    {
        sum += query(u<<1|1, L, R);
        sum %= mod;
    }
    return sum;
}

int main()
{
    cin >> n >> mod;
    build(1, 1, n);
    for(int i = 1; i <= n; ++ i)
    {
        int tp;
        scanf("%d", &tp);
        modify(1, i, i, tp, 1);
    }
    int m;
    cin >> m;
    while(m --)
    {
        int type, l, r;
        scanf("%d%d%d", &type, &l, &r);
        if(type == 1)
        {
            int c;
            scanf("%d", &c);
            modify(1, l, r, 0, c);
        }
        else if(type == 2)
        {
            int c;
            scanf("%d", &c);
            modify(1, l, r, c, 1);
        }
        else
        {
            printf("%d\n", query(1, l, r));
        }
    }
    return 0;
}