区间DP

DP进阶

1、区间DP

将问题分解成为两两合并的形式

解法：对整个问题设最优值，枚举合并点，将问题分解成为左右两个部分，最后将左右两个部分的最优值进行合并得到原问题的最优值。（类似分治）

例1 最大区间和

给N个数，求数组中连续区间数字和最大值，也可以选空区间和为0。

 

上图所示，选取4-5区间最大值为7

如果dp[i-1]+a[i]比a[i]还要小，就舍弃dp[i-1]

状态：dp[i]表示以第i个数结尾的区间的区间和最大值，dp数组最大值为答案，全为负则为0

状态转移方程：dp[i]=max(a[i],a[i]+dp[i-1])

#include<iostream>
#include<math.h>
using namespace std;
int a[101],dp[101];
int n,maxn;
int main(){
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>a[i];
        dp[i]=max(a[i],a[i]+dp[i-1]);
        maxn=max(dp[i],maxn);
    }
    cout<<maxn;
    return 0;
}

优化：

可以发现在状态方程中，dp[i]只与a[i]和上一个dp[i-1]有关，由此可以降低空间复杂度，只用dp和a来循环。

int N,a,dp,ans;
cin>>N;
for(int i=1;i<=N;i++){
    cin>>a;
    dp=max(a,a+dp);
    ans=max(ans,dp);
}

 

例2 P1880 石子合并

https://www.luogu.com.cn/problem/P1880

分析：（区间dp的分析）

• 假设只有2堆石子，显然只有1种合并方案

• 如果有3堆石子，则有2种合并方案，(1,2),3)和(1,(2,3))

···

 

 

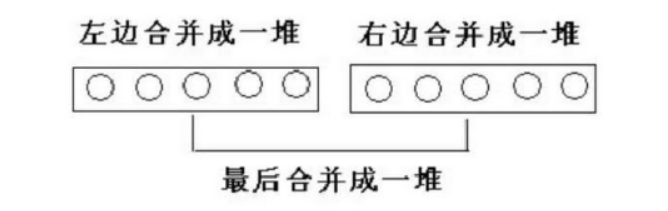
状态：t[i,j]表示从第i堆到第j堆石子数总和

Fmax(i,j)表示将从第i堆石子合并到第j堆石子的最大的划分

Fmin(i,j)表示将从第i堆石子合并到第j堆石子的最小的划分

状态转移方程：

 

 

其中，Fmax[i,i]=0,Fmin[i,i]=0

AC代码：

#include<bits/stdc++.h>
using namespace std;
#define MAXN 0x3f3f3f3f
int N,maxn,minn=MAXN;
int a[105];
int dpmax[405][405],dpmin[405][405],t[405][405];
int main(){
    cin>>N;
    for(int i=1;i<=N;i++){
        cin>>a[i];
        a[i+N]=a[i];
    }
    for(int i=1;i<=N*2;i++){    //因为题目里是一个环，所以要计算到2N
        for(int j=i;j<=N*2;j++){
            t[i][j]=a[j]+t[i][j-1];
        }
    }
    for(int p=1;p<=N-1;p++){    //枚举j-i，并在j-i中枚举k。才能保证递推的正确
        for(int i=1,j=i+p;(j<N*2)&&(i<N*2);i++,j=i+p){
            dpmin[i][j]=MAXN;
            for(int k=i;k<j;k++){
                dpmax[i][j]=max(dpmax[i][k]+dpmax[k+1][j]+t[i][j],dpmax[i][j]);
                dpmin[i][j]=min(dpmin[i][k]+dpmin[k+1][j]+t[i][j],dpmin[i][j]);
            }
        }
    }
    for(int i=1;i<=N;i++){
        maxn=max(maxn,dpmax[i][i+N-1]);
        minn=min(minn,dpmin[i][i+N-1]);
    }
    cout<<minn<<endl<<maxn;
    return 0;
}