OpenMP：实现梯形积分法

 

一、分析什么是梯形积分法

1.分析算法实现思路：

梯形积分法的基本思想是：将x轴上的区间划分为n个等长的子区间。然后计算子区间的和。

2.求出递推公式：

用a和b之间的梯形面积来近似替代a和b之间函数与x轴围成的面积，当a和b之间的区间分的越来越细的时候，近似值就会不断逼近真实值
假设我们把a和b之间的分为n段，则每段距离长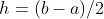
，则之间的任意两个点和之间的面积为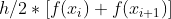
将上述点之间的面积累加求和可以发现，除了两个端点只相加了一次之外，其余的点都被加了两次，因此我们可以得到下面的求和公式：
函数f(x)在[a,b]区间上的积分为：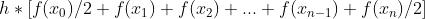

3.写出串行程序：

h = (b - a) / h;
sum = (f(a) + f(b)) / 2;
for (int i = 1; i < n-1; i++){
x_i = a + i * h;
sum += f(x_i);
}
sum = h * sum;

二、OpenMP实现并行化

1.什么是OpenMp：

OpenMP是基于共享内存的编程，不同于MPI，因为是共享内存，所以它不需要将计算结果丢来丢去共享。事实上，我们可以用很少的编译指导语句实现并行，而不需要关心底层的操作。
在OpenMP中，我们常用omp_get_num_threads()函数来获取可用线程个数，用omp_get_thread_num()函数来获得每个线程的ID，为了使用这两个函数，我们需要include <omp.h>。

#pragma omp critical

语句告诉我们各个线程并行执行语句，但当你们执行到critical里面时，要注意有没有其他线程正在里面执行，如果有的话，要等其他线程执行完再进去执行。这样就避免了数据相关的问题，但显而易见，它的执行速度会变低，因为可能存在线程等待的情况。

2.改造程序：梯形积分法OpenMP并行：

#include <stdio.h>
#include <stdlib.h>
#include <omp.h>

double f(double x) {
    return x*x*x + 2*x + 5; 
}
void Trap(double a, double b, int n, double* global_result_p) {
    double h, x, my_result;
    double local_a, local_b;
    int i, local_n;
    int my_rank = omp_get_thread_num();   // 当前线程的ID
    int thread_count = omp_get_num_threads(); // 线程总个数

    h = (b-a)/n;  // h 为每个小梯形的高（底）
    local_n = n/thread_count;  // local_n 为给每个线程分配的梯形数目
    local_a = a + my_rank*local_n*h; // local_a 线程区间的左端点
    local_b = local_a + local_n*h; // local_b 线程区间的右端点
    my_result = (f(local_a) + f(local_b))/2.0; // my_result 对 global_result 贡献的部分和
    for ( i = 1; i <= local_n-1; i++)
    {
        x = local_a + i*h;
        my_result += f(x);
    }
    my_result = my_result*h;

#   pragma omp critical
    *global_result_p += my_result;
    
}

int main(int argc, char* argv[]) {
    double global_result = 0.0;
    double a, b;
    int n;
    int thread_count;

    thread_count = strtol(argv[1], NULL, 10);
    printf("Enter a, b, and n\n");
    scanf("%lf %lf %d", &a, &b, &n);
#   pragma omp parallel num_threads(thread_count)
    Trap(a, b, n, &global_result);

    printf("Thread number is %d.\n", thread_count);
    printf("With n = %d trapezoids, our estimate\n", n);
    printf("of the integral from %f to %f = %.14e.\n", a, b, global_result);
    return 0;
}

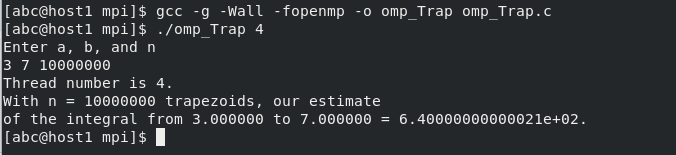
3.运行：梯形积分法OpenMP并行：