常用算法总结
算法面试的准备范围
算法面试的准备范围


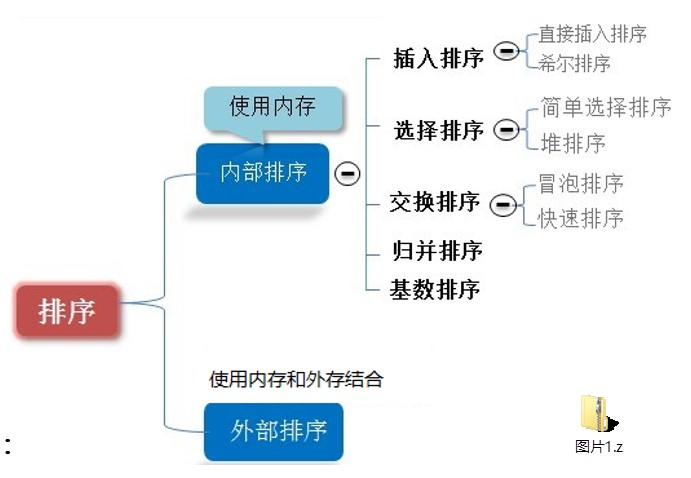
排序算法分类

算法的时间复杂度总结

常见排序算法
冒泡排序

// Java 代码实现
public class BubbleSort implements IArraySort {
@Override
public int[] sort(int[] sourceArray) throws Exception {
// 对 arr 进行拷贝,不改变参数内容
int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
// 外面循环表示 进行了多少轮 即n-1 次循环
for (int i = 1; i < arr.length; i++) {
// 设定一个标记,若为true,则表示此次循环没有进行交换,也就是待排序列已经有序,排序已经完成。
boolean flag = true;
// 每次循环 ,冒泡比较的次数
for (int j = 0; j < arr.length - i; j++) {
if (arr[j] > arr[j + 1]) {
int tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
flag = false;
}
}
if (flag) {
break;
}
}
return arr;
}
}
选择排序

//Java 代码实现
public class SelectionSort implements IArraySort {
@Override
public int[] sort(int[] sourceArray) throws Exception {
int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
// 总共要经过 N-1 轮比较
for (int i = 0; i < arr.length - 1; i++) {
// min 为每轮 假设最小值的下标
int min = i;
// 每轮需要比较的次数 N-i
//每轮 都从i的后一个元素开始比较
for (int j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[min]) {
// 记录目前能找到的最小值元素的索引
min = j;
}
}
// 将找到的最小值和i位置所在的值进行交换
if (i != min) {
int tmp = arr[i];
arr[i] = arr[min];
arr[min] = tmp;
}
}
return arr;
}
}
插入排序
把n个待排序的元素看成为一个有序表和一个无序表,开始时有序表中只包含一个元素,无序表中包含有n-1个元素,排序过程中每次从无序表中取出第一个元素,把它的排序码依次与有序表元素的排序码进行比较,将它插入到有序表中的适当位置,使之成为新的有序表。

//Java 代码实现
public class InsertSort implements IArraySort {
。。
@Override
public int[] sort(int[] sourceArray) throws Exception {
// 对 arr 进行拷贝,不改变参数内容
int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
// 从下标为1的元素开始选择合适的位置插入,因为下标为0的只有一个元素,默认是有序的
for (int i = 1; i < arr.length; i++) {
// 记录要插入的数据
int tmp = arr[i];
// 从已经排序的序列最右边的开始比较,找到比其小的数
int j = i;
//j-1 即带插入元素的前一个元素的下表一定要>=0 ,即j>=1。即j>0
while (j > 0 && tmp < arr[j - 1]) {
// 将j-1 这个位置的元素后移
arr[j] = arr[j - 1];
j--;
}
// 存在比其小的数,插入
if (j != i) {
arr[j] = tmp;
}
}
return arr;
}
}
希尔排序

快速排序

这是采用递归的手段,从数组中 先找到j,把它放到该放的位置,左边小,右边大。 再递归,...
import java.util.*;
public class QuickSort {
// 对arr[l...r]部分进行partition操作
// 返回p, 使得arr[l...p-1] < arr[p] ; arr[p+1...r] > arr[p]
private static int partition(int[] arr, int l, int r){
int v = arr[l];
int j = l; // arr[l+1...j] < v ; arr[j+1...i) > v
// i 表示数组中待遍历的元素
for( int i = l + 1 ; i <= r ; i ++ )
// 如果arrI 大于 v,不用管,直接在后面+1 即可。 如果小,则要变换位置 。
if( arr[i] < v){
j ++;
swap(arr, j, i);
}
swap(arr, l, j);
return j;
}
// 递归使用快速排序,对arr[l...r]的范围进行排序
private static void sort(int[] arr, int l, int r){
if( l >= r )
return;
// 从一堆数组中,找一个元素(第0个),把它放到它该放的位置。返回它的索引
int p = partition(arr, l, r);
sort(arr, l, p-1 );
sort(arr, p+1, r);
}
}
归并排序



import java.text.SimpleDateFormat;
import java.util.Arrays;
import java.util.Date;
public class MergetSort {
public static void main(String[] args) {
int arr[] = { 8, 4, 5, 7, 1, 3, 6, 2 }; //
System.out.println("排序前的时间是=" + date1Str);
int temp[] = new int[arr.length]; //归并排序需要一个额外空间
mergeSort(arr, 0, arr.length - 1, temp);
}
//递归使用 归并排序,将arr[left...right]范围进行排序
public static void mergeSort(int[] arr, int left, int right, int[] temp) {
if(left < right) {
int mid = (left + right) / 2; //中间索引
//向左递归进行分解
mergeSort(arr, left, mid, temp);
//向右递归进行分解
mergeSort(arr, mid + 1, right, temp);
// 此时 ,假设分解成了2部分, 左边一半 有序, 右边一半有序,再进行合并操作
//合并
merge(arr, left, mid, right, temp);
}
}
//合并的方法
/**
*
* @param arr 排序的原始数组
* @param left 左边有序序列的初始索引
* @param mid 中间索引
* @param right 右边索引
* @param temp 做中转的数组
*/
public static void merge(int[] arr, int left, int mid, int right, int[] temp) {
int i = left; // 初始化i, 左边有序序列的初始索引
int j = mid + 1; //初始化j, 右边有序序列的初始索引
int t = 0; // 指向temp数组的当前索引
//(一)
//先把左右两边(有序)的数据按照规则填充到temp数组
//直到左右两边的有序序列,有一边处理完毕为止
while (i <= mid && j <= right) {//继续
//如果左边的有序序列的当前元素,小于等于右边有序序列的当前元素
//即将左边的当前元素,填充到 temp数组
//然后 t++, i++
if(arr[i] <= arr[j]) {
temp[t] = arr[i];
t += 1;
i += 1;
} else { //反之,将右边有序序列的当前元素,填充到temp数组
temp[t] = arr[j];
t += 1;
j += 1;
}
}
//(二)
//把有剩余数据的一边的数据依次全部填充到temp
while( i <= mid) { //左边的有序序列还有剩余的元素,就全部填充到temp
temp[t] = arr[i];
t += 1;
i += 1;
}
while( j <= right) { //右边的有序序列还有剩余的元素,就全部填充到temp
temp[t] = arr[j];
t += 1;
j += 1;
}
//(三)
//将temp数组的元素拷贝到arr
t = 0;
int tempLeft = left; //
while(tempLeft <= right) {
arr[tempLeft] = temp[t];
t += 1;
tempLeft += 1;
}
}
}
排序算法对比

常见查找算法
线性查找
low的一匹,就是根据所以,一个一个去对比

二分查找及其改进

改进,比如 {1,8, 10, 89, 1000, 1000,1234} 当一个有序数组中, 有多个相同的数值时,如何将所有的数值都查找到,比如这里的 1000
//注意:使用二分查找的前提是 该数组是有序的.
public class BinarySearch {
public static void main(String[] args) {
int arr[] = {1, 8, 10, 89, 1000, 1000, 1234};
int resIndex = binarySearch(arr, 0, arr.length - 1, 2);
System.out.println("resIndex=" + resIndex);
}
// 二分查找算法
/**
* @param arr 数组
* @param left 左边的索引
* @param right 右边的索引
* @param findVal 要查找的值
* @return 如果找到就返回下标,如果没有找到,就返回 -1
*/
public static int binarySearch(int[] arr, int left, int right, int findVal) {
// 当 left > right 时,说明递归整个数组,但是没有找到
if (left > right) {
return -1;
}
int mid = (left + right) / 2;
int midVal = arr[mid];
if (findVal > midVal) { // 向 右递归
return binarySearch(arr, mid + 1, right, findVal);
} else if (findVal < midVal) { // 向左递归
return binarySearch(arr, left, mid - 1, findVal);
} else {
return mid;
}
}
//完成一个课后思考题:
/*
* 课后思考题: {1,8, 10, 89, 1000, 1000,1234} 当一个有序数组中,
* 有多个相同的数值时,如何将所有的数值都查找到,比如这里的 1000
*
* 思路分析
* 1. 在找到mid 索引值,不要马上返回
* 2. 向mid 索引值的左边扫描,将所有满足 1000, 的元素的下标,加入到集合ArrayList
* 3. 向mid 索引值的右边扫描,将所有满足 1000, 的元素的下标,加入到集合ArrayList
* 4. 将Arraylist返回
*/
public static List<Integer> binarySearch2(int[] arr, int left, int right, int findVal) {
System.out.println("hello~");
// 当 left > right 时,说明递归整个数组,但是没有找到
if (left > right) {
return new ArrayList<Integer>();
}
int mid = (left + right) / 2;
int midVal = arr[mid];
if (findVal > midVal) { // 向 右递归
return binarySearch2(arr, mid + 1, right, findVal);
} else if (findVal < midVal) { // 向左递归
return binarySearch2(arr, left, mid - 1, findVal);
} else {
// * 思路分析
// * 1. 在找到mid 索引值,不要马上返回
// * 2. 向mid 索引值的左边扫描,将所有满足 1000, 的元素的下标,加入到集合ArrayList
// * 3. 向mid 索引值的右边扫描,将所有满足 1000, 的元素的下标,加入到集合ArrayList
// * 4. 将Arraylist返回
List<Integer> resIndexlist = new ArrayList<Integer>();
//向mid 索引值的左边扫描,将所有满足 1000, 的元素的下标,加入到集合ArrayList
int temp = mid - 1;
while(true) {
if (temp < 0 || arr[temp] != findVal) {//退出
break;
}
//否则,就temp 放入到 resIndexlist
resIndexlist.add(temp);
temp -= 1; //temp左移
}
resIndexlist.add(mid); //
//向mid 索引值的右边扫描,将所有满足 1000, 的元素的下标,加入到集合ArrayList
temp = mid + 1;
while(true) {
if (temp > arr.length - 1 || arr[temp] != findVal) {//退出
break;
}
//否则,就temp 放入到 resIndexlist
resIndexlist.add(temp);
temp += 1; //temp右移
}
return resIndexlist;
}
}
}
插值查找
斐波那契查找

排序算法分类

算法的时间复杂度总结

常见排序算法
冒泡排序

// Java 代码实现
public class BubbleSort implements IArraySort {
@Override
public int[] sort(int[] sourceArray) throws Exception {
// 对 arr 进行拷贝,不改变参数内容
int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
// 外面循环表示 进行了多少轮 即n-1 次循环
for (int i = 1; i < arr.length; i++) {
// 设定一个标记,若为true,则表示此次循环没有进行交换,也就是待排序列已经有序,排序已经完成。
boolean flag = true;
// 每次循环 ,冒泡比较的次数
for (int j = 0; j < arr.length - i; j++) {
if (arr[j] > arr[j + 1]) {
int tmp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = tmp;
flag = false;
}
}
if (flag) {
break;
}
}
return arr;
}
}
选择排序

//Java 代码实现
public class SelectionSort implements IArraySort {
@Override
public int[] sort(int[] sourceArray) throws Exception {
int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
// 总共要经过 N-1 轮比较
for (int i = 0; i < arr.length - 1; i++) {
// min 为每轮 假设最小值的下标
int min = i;
// 每轮需要比较的次数 N-i
//每轮 都从i的后一个元素开始比较
for (int j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[min]) {
// 记录目前能找到的最小值元素的索引
min = j;
}
}
// 将找到的最小值和i位置所在的值进行交换
if (i != min) {
int tmp = arr[i];
arr[i] = arr[min];
arr[min] = tmp;
}
}
return arr;
}
}
插入排序
把n个待排序的元素看成为一个有序表和一个无序表,开始时有序表中只包含一个元素,无序表中包含有n-1个元素,排序过程中每次从无序表中取出第一个元素,把它的排序码依次与有序表元素的排序码进行比较,将它插入到有序表中的适当位置,使之成为新的有序表。

//Java 代码实现
public class InsertSort implements IArraySort {
。。
@Override
public int[] sort(int[] sourceArray) throws Exception {
// 对 arr 进行拷贝,不改变参数内容
int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
// 从下标为1的元素开始选择合适的位置插入,因为下标为0的只有一个元素,默认是有序的
for (int i = 1; i < arr.length; i++) {
// 记录要插入的数据
int tmp = arr[i];
// 从已经排序的序列最右边的开始比较,找到比其小的数
int j = i;
//j-1 即带插入元素的前一个元素的下表一定要>=0 ,即j>=1。即j>0
while (j > 0 && tmp < arr[j - 1]) {
// 将j-1 这个位置的元素后移
arr[j] = arr[j - 1];
j--;
}
// 存在比其小的数,插入
if (j != i) {
arr[j] = tmp;
}
}
return arr;
}
}
希尔排序

快速排序

这是采用递归的手段,从数组中 先找到j,把它放到该放的位置,左边小,右边大。 再递归,...
import java.util.*;
public class QuickSort {
// 对arr[l...r]部分进行partition操作
// 返回p, 使得arr[l...p-1] < arr[p] ; arr[p+1...r] > arr[p]
private static int partition(int[] arr, int l, int r){
int v = arr[l];
int j = l; // arr[l+1...j] < v ; arr[j+1...i) > v
// i 表示数组中待遍历的元素
for( int i = l + 1 ; i <= r ; i ++ )
// 如果arrI 大于 v,不用管,直接在后面+1 即可。 如果小,则要变换位置 。
if( arr[i] < v){
j ++;
swap(arr, j, i);
}
swap(arr, l, j);
return j;
}
// 递归使用快速排序,对arr[l...r]的范围进行排序
private static void sort(int[] arr, int l, int r){
if( l >= r )
return;
// 从一堆数组中,找一个元素(第0个),把它放到它该放的位置。返回它的索引
int p = partition(arr, l, r);
sort(arr, l, p-1 );
sort(arr, p+1, r);
}
}
归并排序



import java.text.SimpleDateFormat;
import java.util.Arrays;
import java.util.Date;
public class MergetSort {
public static void main(String[] args) {
int arr[] = { 8, 4, 5, 7, 1, 3, 6, 2 }; //
System.out.println("排序前的时间是=" + date1Str);
int temp[] = new int[arr.length]; //归并排序需要一个额外空间
mergeSort(arr, 0, arr.length - 1, temp);
}
//递归使用 归并排序,将arr[left...right]范围进行排序
public static void mergeSort(int[] arr, int left, int right, int[] temp) {
if(left < right) {
int mid = (left + right) / 2; //中间索引
//向左递归进行分解
mergeSort(arr, left, mid, temp);
//向右递归进行分解
mergeSort(arr, mid + 1, right, temp);
// 此时 ,假设分解成了2部分, 左边一半 有序, 右边一半有序,再进行合并操作
//合并
merge(arr, left, mid, right, temp);
}
}
//合并的方法
/**
*
* @param arr 排序的原始数组
* @param left 左边有序序列的初始索引
* @param mid 中间索引
* @param right 右边索引
* @param temp 做中转的数组
*/
public static void merge(int[] arr, int left, int mid, int right, int[] temp) {
int i = left; // 初始化i, 左边有序序列的初始索引
int j = mid + 1; //初始化j, 右边有序序列的初始索引
int t = 0; // 指向temp数组的当前索引
//(一)
//先把左右两边(有序)的数据按照规则填充到temp数组
//直到左右两边的有序序列,有一边处理完毕为止
while (i <= mid && j <= right) {//继续
//如果左边的有序序列的当前元素,小于等于右边有序序列的当前元素
//即将左边的当前元素,填充到 temp数组
//然后 t++, i++
if(arr[i] <= arr[j]) {
temp[t] = arr[i];
t += 1;
i += 1;
} else { //反之,将右边有序序列的当前元素,填充到temp数组
temp[t] = arr[j];
t += 1;
j += 1;
}
}
//(二)
//把有剩余数据的一边的数据依次全部填充到temp
while( i <= mid) { //左边的有序序列还有剩余的元素,就全部填充到temp
temp[t] = arr[i];
t += 1;
i += 1;
}
while( j <= right) { //右边的有序序列还有剩余的元素,就全部填充到temp
temp[t] = arr[j];
t += 1;
j += 1;
}
//(三)
//将temp数组的元素拷贝到arr
t = 0;
int tempLeft = left; //
while(tempLeft <= right) {
arr[tempLeft] = temp[t];
t += 1;
tempLeft += 1;
}
}
}
排序算法对比

常见查找算法
线性查找
low的一匹,就是根据所以,一个一个去对比

二分查找及其改进

改进,比如 {1,8, 10, 89, 1000, 1000,1234} 当一个有序数组中, 有多个相同的数值时,如何将所有的数值都查找到,比如这里的 1000
//注意:使用二分查找的前提是 该数组是有序的.
public class BinarySearch {
public static void main(String[] args) {
int arr[] = {1, 8, 10, 89, 1000, 1000, 1234};
int resIndex = binarySearch(arr, 0, arr.length - 1, 2);
System.out.println("resIndex=" + resIndex);
}
// 二分查找算法
/**
* @param arr 数组
* @param left 左边的索引
* @param right 右边的索引
* @param findVal 要查找的值
* @return 如果找到就返回下标,如果没有找到,就返回 -1
*/
public static int binarySearch(int[] arr, int left, int right, int findVal) {
// 当 left > right 时,说明递归整个数组,但是没有找到
if (left > right) {
return -1;
}
int mid = (left + right) / 2;
int midVal = arr[mid];
if (findVal > midVal) { // 向 右递归
return binarySearch(arr, mid + 1, right, findVal);
} else if (findVal < midVal) { // 向左递归
return binarySearch(arr, left, mid - 1, findVal);
} else {
return mid;
}
}
//完成一个课后思考题:
/*
* 课后思考题: {1,8, 10, 89, 1000, 1000,1234} 当一个有序数组中,
* 有多个相同的数值时,如何将所有的数值都查找到,比如这里的 1000
*
* 思路分析
* 1. 在找到mid 索引值,不要马上返回
* 2. 向mid 索引值的左边扫描,将所有满足 1000, 的元素的下标,加入到集合ArrayList
* 3. 向mid 索引值的右边扫描,将所有满足 1000, 的元素的下标,加入到集合ArrayList
* 4. 将Arraylist返回
*/
public static List<Integer> binarySearch2(int[] arr, int left, int right, int findVal) {
System.out.println("hello~");
// 当 left > right 时,说明递归整个数组,但是没有找到
if (left > right) {
return new ArrayList<Integer>();
}
int mid = (left + right) / 2;
int midVal = arr[mid];
if (findVal > midVal) { // 向 右递归
return binarySearch2(arr, mid + 1, right, findVal);
} else if (findVal < midVal) { // 向左递归
return binarySearch2(arr, left, mid - 1, findVal);
} else {
// * 思路分析
// * 1. 在找到mid 索引值,不要马上返回
// * 2. 向mid 索引值的左边扫描,将所有满足 1000, 的元素的下标,加入到集合ArrayList
// * 3. 向mid 索引值的右边扫描,将所有满足 1000, 的元素的下标,加入到集合ArrayList
// * 4. 将Arraylist返回
List<Integer> resIndexlist = new ArrayList<Integer>();
//向mid 索引值的左边扫描,将所有满足 1000, 的元素的下标,加入到集合ArrayList
int temp = mid - 1;
while(true) {
if (temp < 0 || arr[temp] != findVal) {//退出
break;
}
//否则,就temp 放入到 resIndexlist
resIndexlist.add(temp);
temp -= 1; //temp左移
}
resIndexlist.add(mid); //
//向mid 索引值的右边扫描,将所有满足 1000, 的元素的下标,加入到集合ArrayList
temp = mid + 1;
while(true) {
if (temp > arr.length - 1 || arr[temp] != findVal) {//退出
break;
}
//否则,就temp 放入到 resIndexlist
resIndexlist.add(temp);
temp += 1; //temp右移
}
return resIndexlist;
}
}
}
插值查找



 浙公网安备 33010602011771号
浙公网安备 33010602011771号