2025.10.24D 开会 题解
我要造福人类!!!
大抽象题,非常佩服某位场切本题的大佬。
考虑我们可以按照字符串长度分成 50 组考虑,对于长度相同的字符串,将它合并即可。记 \(num_{i,j}=\sum\limits_{l_k=i}[s_{k,j}=O]\)。
显然有一个只能拿 20pts 的暴力做法,即只计算循环节。但由于循环节太巨了存不下,考虑退而求其次,选择一个大部分数的循环节 \(M=2^4\times 3^2\times 5\times 7=5040\)。除了 \(A=\{11,13,17,19,22,23,25,26,27,29,31,32,33,34,37,38,39,41,43,44,46,47,49,50\}\) 集合内的数以外,其他都能整除这个循环节?
这个循环节有什么性质呢?设 \(x\in A\),则 \(\dfrac{x}{\gcd(M,x)}\) 为质数。所以我们可以将这个长度为 \(M\) 的循环节扩展成一个 \(\operatorname{lcm}(x,M)\) 的循环节,然后再压缩成一个长为 \(M\) 的循环节。由于此时循环节的每个位置可能代表实际循环节不同的位置,所以人数可能不同,因此需要在循环节的每个位置都建一个数组 \(tg_{i,j}\),记录 \(i\) 位置有 \(j\) 个人的方案数。同时,我们需要一个辅助数组 \(tmp_{i,j}\),表示在扩展后循环节上第 \(i\) 个位置有 \(j\) 个人的方案数,则有计算公式:
大致如下图:
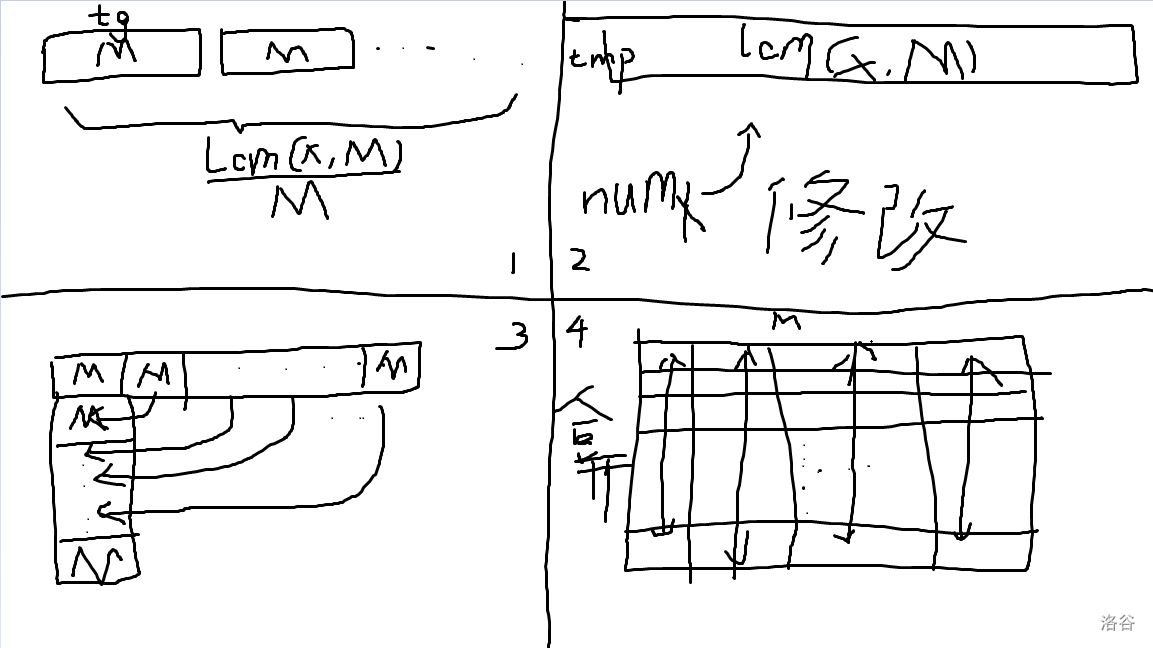
实际上理论来说是需要乘一些东西的,不过由于都乘了,而 \(\operatorname{lcm}\limits_{i=1}^{50}i|50!\),所以可以当作都没乘。同时上面的 \(tmp\) 数组大小也可以优化为 \(nM\)。
这样的话,\(27,29,31,32,37,41,43,47,49\) 的问题就都解决了。但是我们会发现,\(11,22,33,44\),\(13,26,39\),\(17,34\),\(19,38\),\(23,46\),\(25,50\) 之间依然存在冲突。究其原因,在于其 \(\dfrac{x}{\gcd(x,M)}\) 存在相同情况。对于这种情况,以 \(11\) 一组为例,我们可以将它们统一改成 \(132\)(也就是它们的最小公倍数),这样就只需要修改一次,冲突就不存在了。其他的同理。
在得到 \(tg\) 之后就好办了,具体见代码。
时间复杂度 \(O(Mn\max (l))\)。不过好像有神秘方法可以将 \(M\) 改为 \(2^4\times 3^2\times 5=720\),但是不会。但现在(2025.10.26)会了。考虑质数的本质实际上是 \(\gcd=1\)。那么我们就没有必要纠结于 \(\dfrac{x}{\gcd(M,x)}\) 是否是一个质数了。所以我们可以将 \(7\) 从 \(M\) 中取出,同时相应的将 \(7,14,21,28,35,42,49\) 全部归到 \(2940\),就可以优化时间复杂度了。按照这个思路,我们可以将 \(5,3\) 甚至 \(2\) 拆出,但是从 \(5\) 开始 \(\operatorname{lcm}_{5|i}i\) 就已经大于 \(10^4\) 了,还不如不优化,所以可以停止了。
//5040版
#include<bits/stdc++.h>
using namespace std;
const int N=55,M=5040,K=505,p=1e9+7;string s;
int n,num[K][K],vs[K],tg[M][K],tmp[M][K],ans[K],sum;
inline int qpow(int x,int y){
int re=1;
while(y){
if(y&1) re=1ll*re*x%p;
x=1ll*x*x%p,y>>=1;
}return re;
}inline int md(int x){if(x>=p) x-=p;return x;}
signed main(){
freopen("meeting.in","r",stdin);
freopen("meeting.out","w",stdout);
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0),cin>>n;
for(int i=0;i<M;i++) tg[i][0]=1;
for(int i=1,m;i<=n;i++){
cin>>m>>s;string t=s;int ls=m;
if(m%11==0) while(m<132) s+=t,m+=ls;
else if(m%13==0) while(m<78) s+=t,m+=ls;
else if(m%17==0) while(m<34) s+=t,m+=ls;
else if(m%19==0) while(m<38) s+=t,m+=ls;
else if(m%23==0) while(m<46) s+=t,m+=ls;
else if(m%25==0) while(m<50) s+=t,m+=ls;
s=" "+s;for(int j=1;j<=m;j++)
num[m][j%m]+=(s[j]=='O'),vs[m]|=(s[j]=='O');
}for(int i=1;i<=150;i++) if(vs[i]){
int lc=M*i/__gcd(i,M);
for(int j=0,cc=0;j<lc;j++,cc=j%M) for(int k=num[i][j%i];k<=n;k++)
tmp[cc][k]=md(tmp[cc][k]+tg[cc][k-num[i][j%i]]);
for(int j=0;j<M;j++) for(int k=0;k<=n;k++) tg[j][k]=tmp[j][k],tmp[j][k]=0;
}for(int i=0;i<M;i++) for(int j=0;j<=n;j++)
ans[j]=md(ans[j]+tg[i][j]),sum=md(sum+tg[i][j]);
sum=qpow(sum,p-2);for(int i=1;i<=50;i++) sum=1ll*sum*i%p;
for(int i=1;i<=n;i++) cout<<1ll*ans[i]*sum%p<<"\n";
return 0;
}
//720版
#include<bits/stdc++.h>
using namespace std;
const int N=3005,M=720,K=505,p=1e9+7;string s;
int n,num[N][N],vs[N],tg[M][K],tmp[M][K],ans[K],sum;
inline int qpow(int x,int y){
int re=1;
while(y){
if(y&1) re=1ll*re*x%p;
x=1ll*x*x%p,y>>=1;
}return re;
}inline int md(int x){if(x>=p) x-=p;return x;}
signed main(){
freopen("meeting.in","r",stdin);
freopen("meeting.out","w",stdout);
ios::sync_with_stdio(0);
cin.tie(0),cout.tie(0),cin>>n;
for(int i=0;i<M;i++) tg[i][0]=1;
for(int i=1,m;i<=n;i++){
cin>>m>>s;string t=s;int cc=m;
if(m%7==0) while(m<2940) s+=t,m+=cc;
else if(m%11==0) while(m<132) s+=t,m+=cc;
else if(m%13==0) while(m<78) s+=t,m+=cc;
else if(m%17==0) while(m<34) s+=t,m+=cc;
else if(m%19==0) while(m<38) s+=t,m+=cc;
else if(m%23==0) while(m<46) s+=t,m+=cc;
else if(m%25==0) while(m<50) s+=t,m+=cc;
s=" "+s;for(int j=1;j<=m;j++)
num[m][j%m]+=(s[j]=='O'),vs[m]|=(s[j]=='O');
}for(int i=1;i<=2940;i++) if(vs[i]){
int lc=M*i/__gcd(i,M);
for(int j=0,cc=0;j<lc;j++,cc=j%M) for(int k=num[i][j%i];k<=n;k++)
tmp[cc][k]=md(tmp[cc][k]+tg[cc][k-num[i][j%i]]);
for(int j=0;j<M;j++) for(int k=0;k<=n;k++) tg[j][k]=tmp[j][k],tmp[j][k]=0;
}for(int i=0;i<M;i++) for(int j=0;j<=n;j++)
ans[j]=md(ans[j]+tg[i][j]),sum=md(sum+tg[i][j]);
sum=qpow(sum,p-2);for(int i=1;i<=50;i++) sum=1ll*sum*i%p;
for(int i=1;i<=n;i++) cout<<1ll*ans[i]*sum%p<<"\n";
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号