编辑距离

题目

思路解析

1.要了解思路需要看下图:

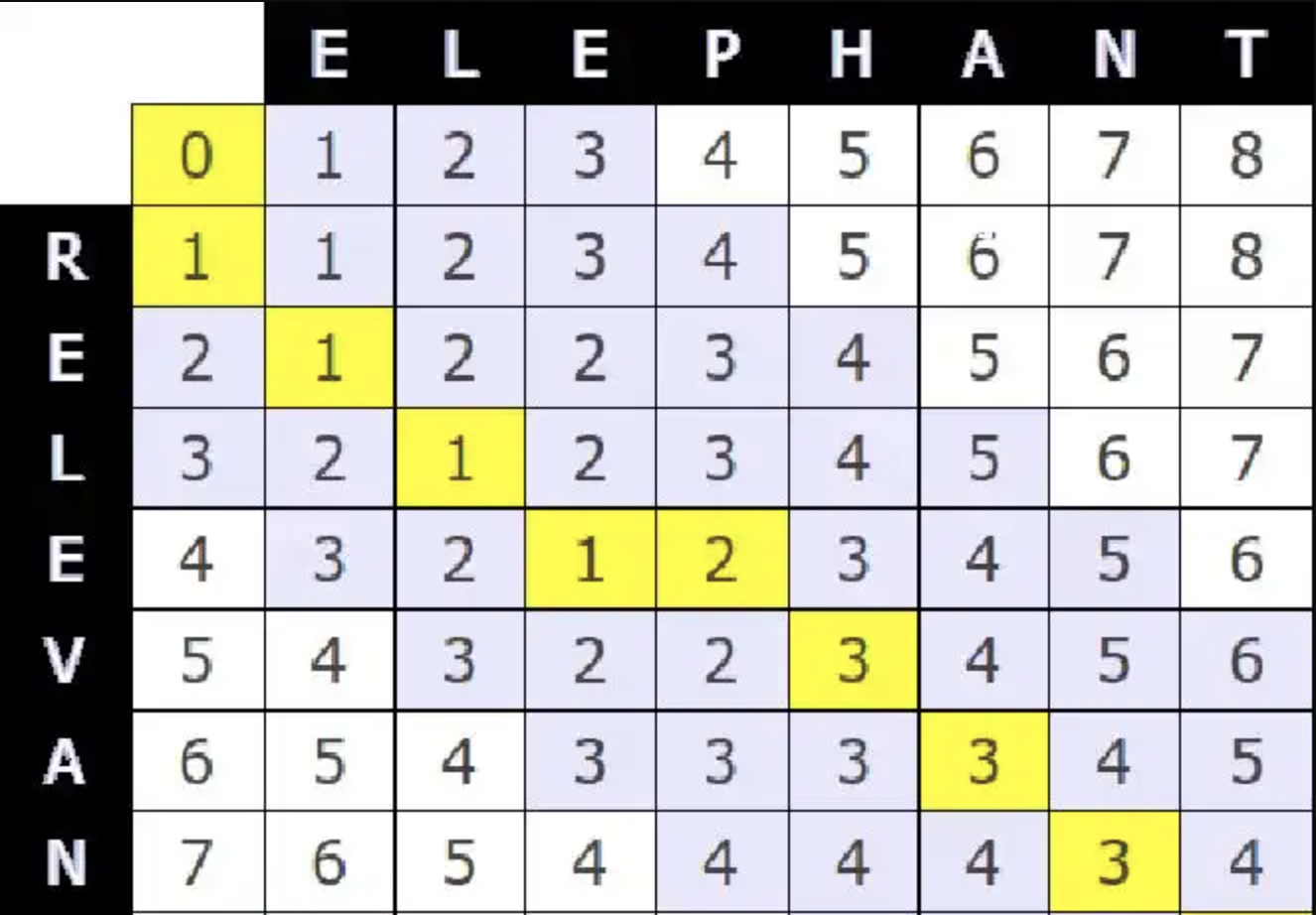
这里面充分展示了,删除,插入和替换的做法的次数.如第一行和第一列,分别都代表着空字符串转换成上边和左边的字符串的步数,

因为是空字符串,所以只能是插入的方式,所以步数是不断递增的

如果字符串是rel那么就应该是

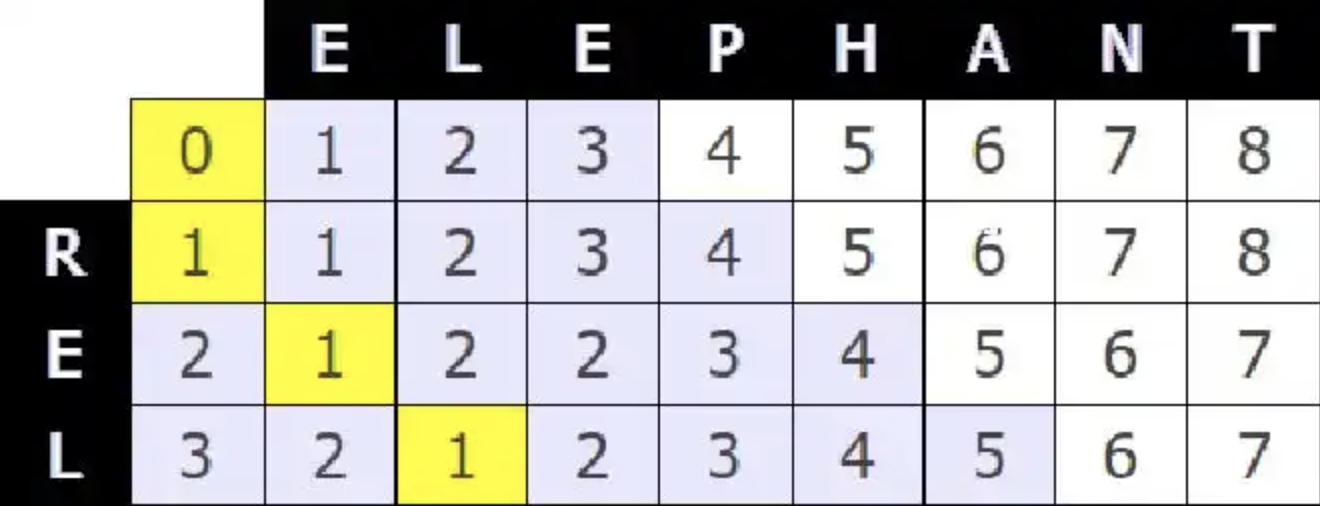
 应为当字符串是r的时候,对于空的位置,需要的是删除,所以操作是1,对于e的位置的是替换(这是延续上一步操作进行+1的,也就是0+1)

 应为当字符串是e的时候,对于空的位置,需要的是删除,所以操作是2[因为需要延续 r 时候操作],对于e的位置的是一致的,所以可以不进行操作,则需要对之前的进行继承就是 [i-1][j-1] 的位置

当时左边第三个字符 L 的时候,对于上边的第二个也是一样的,故也是继承之前的位置, 至此 REL 转为 EL便都结束了,其中需要的就是删除R [这是对于REL 来说的 ,对于 EL 来说应该是插入]

代码展示

private static int min(int a,int b,int c){
    return Math.min(a,Math.min(b,c));
}

public static int minDistance(String word1, String word2) {
    int l1 = word1.length();
    int l2 = word2.length();

    int[][] dp = new int[l1+1][l2+1];
    for (int i = 0; i <= l2; i++){
        dp[0][i] = i;
    }

    for (int i = 0; i <= l1; i++){
        dp[i][0] = i;
    }

    for (int i = 1; i <= l1; i++){
        for (int j = 1; j <= l2; j++){
            if (word1.charAt(i-1) == word2.charAt(j-1)){
                // 如果相同则代表不需要进行额外操作,直接延续两个字符比对的上一步的结果
                dp[i][j] = dp[i-1][j-1];
            }else {
                // 如果当前字符不同，
                // 则当前单元格的值等于左上角单元格的值加上1，
                // 或者等于左侧单元格的值加1（删除操作），
                // 或者等于上侧单元格的值加1（插入操作），
                // 取这三种情况的最小值
                // dp[i-1][j] #删除
                // dp[i][j-1] #插入
                // dp[i-1][j-1] #替换
                dp[i][j] = min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1])+1;
            }
        }
    }

//        System.out.println(Arrays.deepToString(dp));
    return dp[l1][l2];
}

 

关联说明