934. 最短的桥

题目：

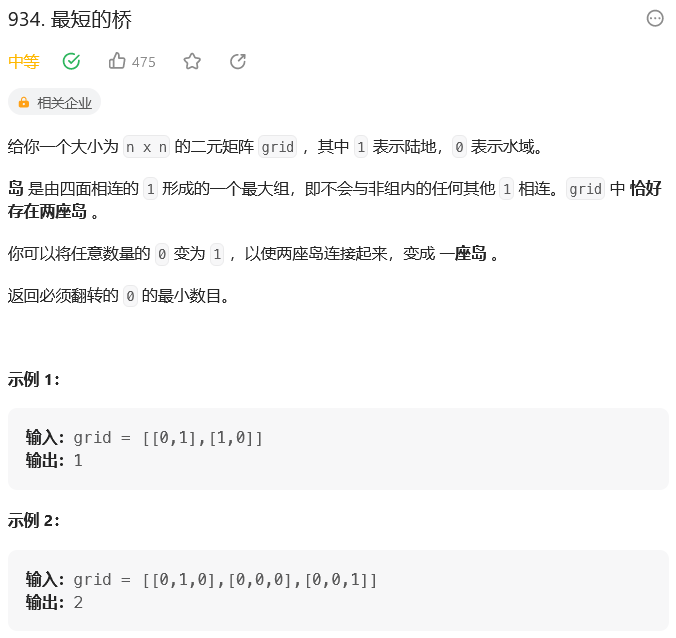
思路：

【1】利用深度优先搜索求出其中的一座岛，然后利用广度优先搜索来找到两座岛的最短距离

我们通过遍历找到数组 grid 中的 1 后进行深度优先搜索，此时可以得到第一座岛的位置集合，记为 island，并将其位置全部标记为 −1。
随后我们从 island 中的所有位置开始进行广度优先搜索，当它们到达了任意的 1 时，即表示搜索到了第二个岛，搜索的层数就是答案

 

代码展示：

//时间6 ms 击败 93.52%
//内存43 MB 击败 27.46%
//时间复杂度：O(n^2)，其中 n 表示 grid 的行数，grid 的行数与列数相等。
//我们只需遍历一遍矩阵即可完成访问两个不同的岛。
//空间复杂度：O(n^2)。其中 n 表示 grid 的行数，grid 的行数与列数相等。
//grid 中每个岛含有的元素最多为 n^2 个，广度优先搜索时队列中最多有 n^2 个元素，因此空间复杂度为 O(n^2)。
class Solution {
    public int shortestBridge(int[][] grid) {
        int n = grid.length;
        int[][] dirs = {{-1, 0}, {1, 0}, {0, 1}, {0, -1}};

        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] == 1) {
                    Queue<int[]> queue = new ArrayDeque<int[]>();
                    dfs(i, j, grid, queue);
                    int step = 0;
                    while (!queue.isEmpty()) {
                        int sz = queue.size();
                        for (int k = 0; k < sz; k++) {
                            int[] cell = queue.poll();
                            int x = cell[0], y = cell[1];
                            for (int d = 0; d < 4; d++) {
                                int nx = x + dirs[d][0];
                                int ny = y + dirs[d][1];
                                if (nx >= 0 && ny >= 0 && nx < n && ny < n) {
                                    if (grid[nx][ny] == 0) {
                                        queue.offer(new int[]{nx, ny});
                                        grid[nx][ny] = -1;
                                    } else if (grid[nx][ny] == 1) {
                                        return step;
                                    }
                                }
                            }
                        }
                        step++;
                    }
                }
            }
        }
        return 0;
    }

    public void dfs(int x, int y, int[][] grid, Queue<int[]> queue) {
        if (x < 0 || y < 0 || x >= grid.length || y >= grid[0].length || grid[x][y] != 1) {
            return;
        }
        queue.offer(new int[]{x, y});
        grid[x][y] = -1;
        dfs(x - 1, y, grid, queue);
        dfs(x + 1, y, grid, queue);
        dfs(x, y - 1, grid, queue);
        dfs(x, y + 1, grid, queue);
    }
}


//时间5 ms 击败 98.70%
//内存42.8 MB 击败 47.15%
class Solution {
    public int shortestBridge(int[][] grid) {
        Deque<int[]>edges=new LinkedList<>();//记录不是岛屿的位置
        //先利用bfs对整个网格进行标记，并将标记过的岛屿记为2 bfs广搜
        A:
        for(int i=0;i<grid.length;i++){
            for(int j=0;j<grid[0].length;j++){
                if(grid[i][j]==1){
                    bfs(grid,i,j,edges);
                    break A;
                }
            }
        }
        //判断最短路径
        int ans=0;//循环次数最短的几位最短路径
        while(panduan(grid,edges))ans++;//对不是岛屿的位置进行搜索找到最近标记过的岛屿位置
        return ans;
    }
    public boolean panduan(int[][]grid,Deque<int[]>edges){
        int length=edges.size();
        for(int i=0;i<length;i++){
            //
            int []point=edges.poll();
            int x=point[0],y=point[1];
            if(x>0){
                if(grid[x-1][y]==0){
                    grid[x-1][y]=2;
                    edges.add(new int[]{x-1,y});
                }else if(grid[x-1][y]==1){
                    return false;
                }
            }
            if(x<grid.length-1){
                if(grid[x+1][y]==0){
                    grid[x+1][y]=2;
                    edges.add(new int[]{x+1,y});
                }else if(grid[x+1][y]==1){
                    return false;
                }
            }
            if(y>0){
                if(grid[x][y-1]==0){
                    grid[x][y-1]=2;
                    edges.add(new int[]{x,y-1});
                }else if(grid[x][y-1]==1){
                    return false;
                }
            }
            if(y<grid.length-1){
                if(grid[x][y+1]==0){
                    grid[x][y+1]=2;
                    edges.add(new int[]{x,y+1});
                }else if(grid[x][y+1]==1){
                    return false;
                }
            }
        }
        return true;
    }
    public void bfs(int [][]grid,int x,int y, Deque<int[]>edges){
        grid[x][y]=2;//对我们搜索过的点进行标记
        boolean ed=false;
        //对是1的不停的bfs知道搜索到周围不在有1的进入到else将此次位置记录到edges中
        if(x>0&&grid[x-1][y]==1)bfs(grid,x-1,y,edges);
        else ed=true;
        if(x<grid.length-1&&grid[x+1][y]==1)bfs(grid,x+1,y,edges);
         else ed=true;
        if(y>0&&grid[x][y-1]==1)bfs(grid,x,y-1,edges);
         else ed=true;
        if(y<grid.length-1&&grid[x][y+1]==1)bfs(grid,x,y+1,edges);
         else ed=true;
         if(ed)edges.add(new int[]{x,y});//将为0的店添加进队列内，等待判断最短路径
    }
}