剑指 Offer II 010. 和为 k 的子数组（560. 和为 K 的子数组）

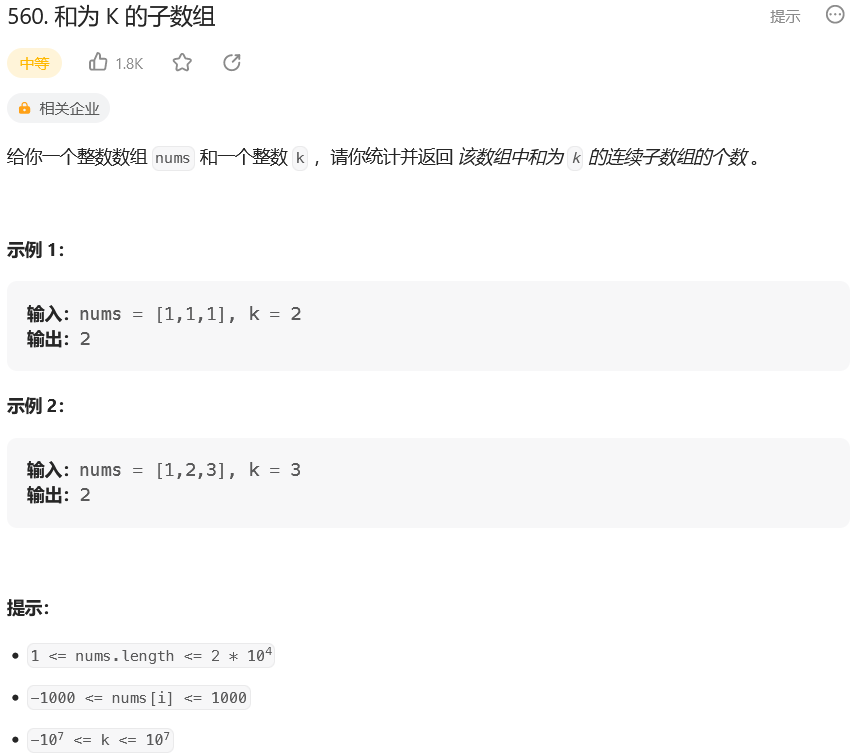
题目：

 

思路：

【1】暴力破解，双循环遍历列举；

【2】前缀和 + 哈希表优化

这种解法是依据题目中的 连续子数组 这个条件
假设 b位置到a位置 的汇总和是符合条件的（b > a）
那么必然有 （ 0-b的汇总和） - （0-a的汇总和）= k
依据这种我们只需要知道差值的汇总和有多少个那么该位置就存在多少种可能，组成连续子数组

 

代码展示：

前缀和 + 哈希表优化的方式：

//时间21 ms击败82.45%
//内存44 MB击败82.20%
//时间复杂度：O(n)，其中 n 为数组的长度。
//空间复杂度：O(n)，其中 n 为数组的长度。
class Solution {
    public int subarraySum(int[] nums, int k) {
        int count = 0, pre = 0;
        HashMap < Integer, Integer > mp = new HashMap < > ();
        mp.put(0, 1);
        for (int i = 0; i < nums.length; i++) {
            pre += nums[i];
            if (mp.containsKey(pre - k)) {
                count += mp.get(pre - k);
            }
            mp.put(pre, mp.getOrDefault(pre, 0) + 1);
        }
        return count;
    }
}

 

暴力破解的方式：

//时间1947 ms击败5.5%
//内存45 MB击败61.37%
//时间复杂度：O(n^2)，其中 n 为数组的长度。
//空间复杂度：O(1)。
class Solution {
    public int subarraySum(int[] nums, int k) {
        int count = 0;
        for (int start = 0; start < nums.length; ++start) {
            int sum = 0;
            for (int end = start; end >= 0; --end) {
                sum += nums[end];
                if (sum == k) {
                    count++;
                }
            }
        }
        return count;
    }
}