剑指 Offer 19. 正则表达式匹配（10. 正则表达式匹配）

题目：

 

 

 

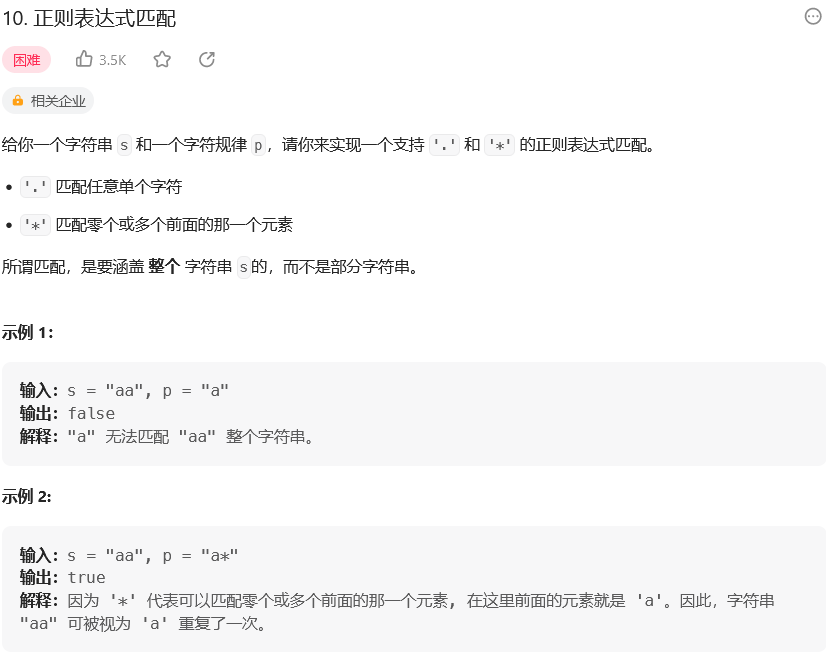
思路：

【1】动态规划

 

【2】递归的方式

代码展示：

递归的方式（但是性能不佳）：

//时间93 ms击败5.3%
//内存41.6 MB击败6.94%
class Solution {
    public boolean isMatch(String s, String p) {
        // 如果字符串长度为0，需要检测下正则串
        if (s.length() == 0) {
            // 如果正则串长度为奇数，必定不匹配，比如 "."、"ab*",必须是 a*b*这种形式，*在奇数位上
            if (p.length() % 2 != 0) return false;
            int i = 1;
            while (i < p.length()) {
                if (p.charAt(i) != '*') return false;
                i += 2;
            }
            return true;
        }
        // 如果字符串长度不为0，但是正则串没了，return false
        if (p.length() == 0) return false;
        // c1 和 c2 分别是两个串的当前位，c3是正则串当前位的后一位，如果存在的话，就更新一下
        char c1 = s.charAt(0), c2 = p.charAt(0), c3 = 'a';
        if (p.length() > 1) {
            c3 = p.charAt(1);
        }
        // 和dp一样，后一位分为是 '*' 和不是 '*' 两种情况
        if (c3 != '*') {
            // 如果该位字符一样，或是正则串该位是 '.',也就是能匹配任意字符，就可以往后走
            if (c1 == c2 || c2 == '.') {
                return isMatch(s.substring(1), p.substring(1));
            } else {
                // 否则不匹配
                return false;
            }
        } else {
            // 如果该位字符一样，或是正则串该位是 '.'，和dp一样，有看和不看两种情况
            if (c1 == c2 || c2 == '.') {
                return isMatch(s.substring(1), p) || isMatch(s, p.substring(2));
            } else {
                // 不一样，那么正则串这两位就废了，直接往后走
                return isMatch(s, p.substring(2));
            }
        }
    }
}

 

动态规划的方式：

//时间1 ms击败100%
//内存40 MB击败71.87%
//时间复杂度：O(mn)，其中 m 和 n 分别是字符串 s 和 p 的长度。
//我们需要计算出所有的状态，并且每个状态在进行转移时的时间复杂度为 O(1)。
//空间复杂度：O(mn)，即为存储所有状态使用的空间。
class Solution {
    public boolean isMatch(String s, String p) {
        int m = s.length() + 1, n = p.length() + 1;
        boolean[][] dp = new boolean[m][n];
        //代表两个空字符串能够匹配
        dp[0][0] = true;

        // 初始化首行
        // 这一行是为了特殊处理，当字符串为空串时，是否能和正则表达式匹配
        // 首行 s 为空字符串，因此当 p 的偶数位为 * 时才能够匹配（即让 p 的奇数位出现 0 次，保持 p 是空字符串）。
        // 因此，循环遍历字符串 p ，步长为 2（即只看偶数位）
        for(int j = 2; j < n; j += 2){
            dp[0][j] = dp[0][j - 2] && p.charAt(j - 1) == '*';
        }

        // 状态转移
        for(int i = 1; i < m; i++) {
            for(int j = 1; j < n; j++) {
                if(p.charAt(j - 1) == '*') {
                    if(dp[i][j - 2]) dp[i][j] = true;
                    // 让字符 p[j - 2] 多出现 1 次时，能否匹配；
                    else if(dp[i - 1][j] && s.charAt(i - 1) == p.charAt(j - 2)) dp[i][j] = true;
                    // 让字符 '.' 多出现 1 次时，能否匹配；
                    else if(dp[i - 1][j] && p.charAt(j - 2) == '.') dp[i][j] = true;
                } else {
                    // 即让字符 p[j - 1] 多出现一次时，能否匹配；
                    if(dp[i - 1][j - 1] && s.charAt(i - 1) == p.charAt(j - 1)) dp[i][j] = true;
                    //将字符 . 看作字符 s[i - 1] 时，能否匹配；
                    else if(dp[i - 1][j - 1] && p.charAt(j - 1) == '.') dp[i][j] = true;
                }
            }
        }

        return dp[m - 1][n - 1];
    }
}

代码简化一下：
//时间1 ms击败100%
//内存40.1 MB击败60.18%
class Solution {

    public boolean isMatch(String s, String p) {

        int m = s.length() + 1, n = p.length() + 1;
        boolean[][] dp = new boolean[m][n];
        dp[0][0] = true;
        for(int j = 2; j < n; j += 2) dp[0][j] = dp[0][j - 2] && p.charAt(j - 1) == '*';

        for(int i = 1; i < m; i++) {
            for(int j = 1; j < n; j++) {
                dp[i][j] = p.charAt(j - 1) == '*' ?
                    dp[i][j - 2] || dp[i - 1][j] && (s.charAt(i - 1) == p.charAt(j - 2) || p.charAt(j - 2) == '.') :
                    dp[i - 1][j - 1] && (p.charAt(j - 1) == '.' || s.charAt(i - 1) == p.charAt(j - 1));

            }

        }

        return dp[m - 1][n - 1];

    }

}