【论文笔记】Exploiting Support Vector Machine Algorithm to Break the Secret Key(开题报告使用)

题目：Exploiting Support Vector Machine Algorithm to Break the Secret Key/利用支持向量机算法破解密钥

作者：Shourong HOU, Yujie ZHOU, Hongming LIU, Nianhao ZHU

来源：RADIOENGINEERING（4区）, VOL. 27, NO. 1, APRIL 2018 

标签：Power analysis, support vector machine, synthetic minority oversampling technique, Hamming Weight class

摘要：模板攻击（TA）和支持向量机（SVM）是侧信道攻击（SCA）的两种有效方法。几乎所有关于SCA中SVM的研究都假定所需的能量迹是足够的，这也意味着属于每个类的能量迹的数量是相等的。事实上，在真实的攻击场景中，由于各种限制，可能没有足够的能量迹。更具体地说，S-Box输出的汉明权重导致9个二项式分布类，与均匀分布类相比，这显著降低了SVM的性能。本文首先详细探讨了类别的分布对SVM性能的影响。此外，我们还进行了合成少数过采样技术（SMOTE），以解决由二项式分布类引起的问题。通过使用SMOTE，在测试阶段提高了SVM的成功率，并且SVM需要较少的功率跟踪来恢复密钥。此外，选择TA作为比较。与在非限制场景中被视为常识的情况相反，我们的结果表明，具有适当参数的SVM可以显著优于TA。

1.简介

2.背景

2.1分析攻击

2.2了解SVM

3.方法

　　数据：为了确保结果的再现性，我们使用了一个公开的数据集。DPA竞赛v4（DPACv4.1）[24]提供了掩蔽AES软件实现的10w个功率跟踪。由于掩码值在[16]中是已知的，我们可以直接将该数据集转换为未受保护的场景。我们选择了4000（DS0）和8000（DS1）个随机功率迹线，以对所有实验进行公平比较。而且，我们只探索了如何更有效地恢复密钥，而忽略了掩码恢复阶段。

　　我们的实验方法如下：
　　在给定测试集的情况下，有三分之二被用作学习集，剩下的三分之一被保留为测试集。通过使用10倍交叉验证，将学习集分为训练集和验证集。所有折叠的验证集用于参数调整阶段。在测试阶段，使用最佳参数（在所有验证折叠上具有最高平均精度的参数）来训练最终的SVM模型。此外，在密钥恢复阶段通过最大似然估计获得正确的密钥。

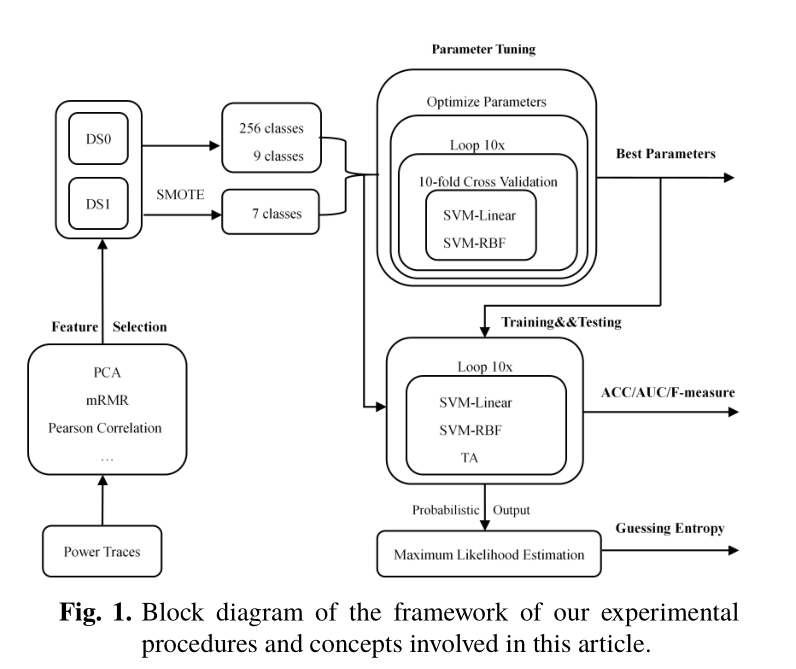
　　图1说明了本文中涉及的实验过程和概念的框架。SMOTE用于在执行功能选择后补偿二项式分布式硬件类。参数调整阶段为训练和测试阶段找到最佳参数。每个实验在循环块中重复十次。测试结果以ACC/AveP/F测量的形式给出。猜测属性用于评估剩余钥匙的数量。

 

 

 

3.1特征选择

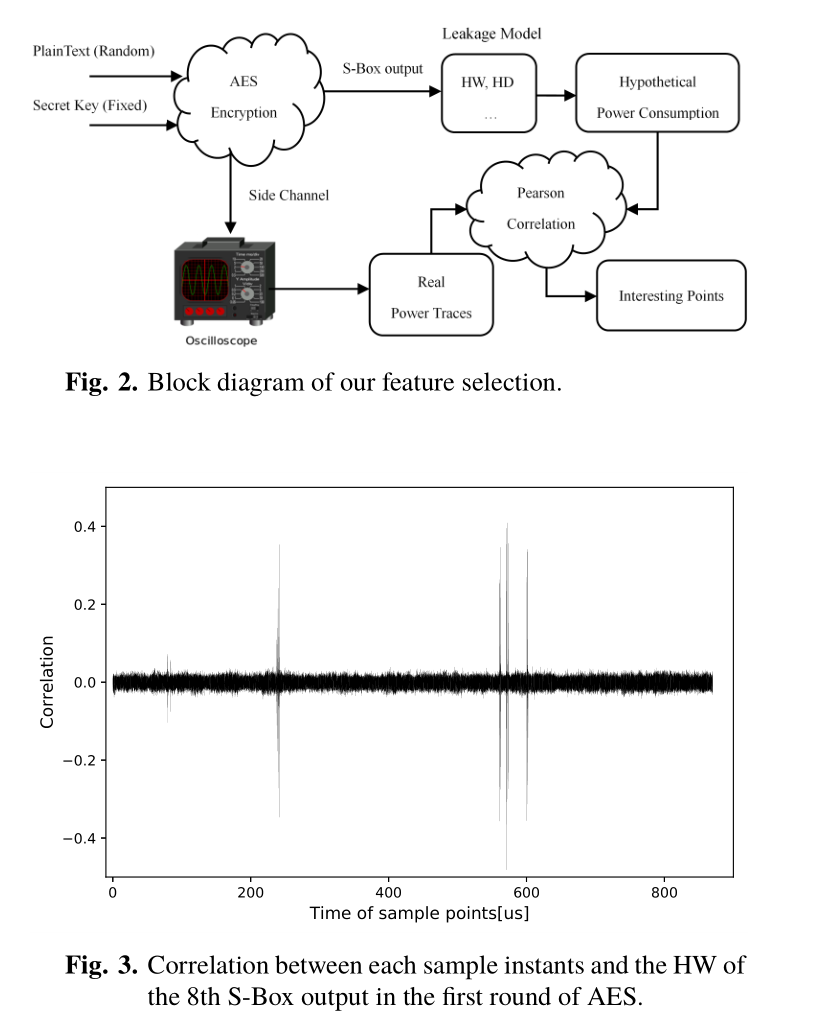
　　我们的数据集中在AES第一轮密钥的所有字节（0到15）上。尽管它是一个软件实现，但最泄漏的操作不是寄存器读取或写入，而是第一轮AES的SBox操作。如图2所示，HW模型用于描述S-Box输出的假设功耗。S-Box输出的HW值，即HW（Sbox[ti⊕ ki]），i＝0,1...，15被选择为SVM分类器的标签。这里，ti表示随机明文的第i个字节，ki表示固定密钥的第i字节，Sbox[·]是替换操作。因此，SVM分类器的标签值对应于从0到8的HW值。在这种情况下，属于每个HW类的功率迹线的数量服从二项式分布。
　　根据文章[16]，兴趣点是从16个S盒中提取的。我们计算了功率迹线的每个采样瞬间和S-Box输出的HW之间的皮尔逊相关系数，以定位感兴趣的点。
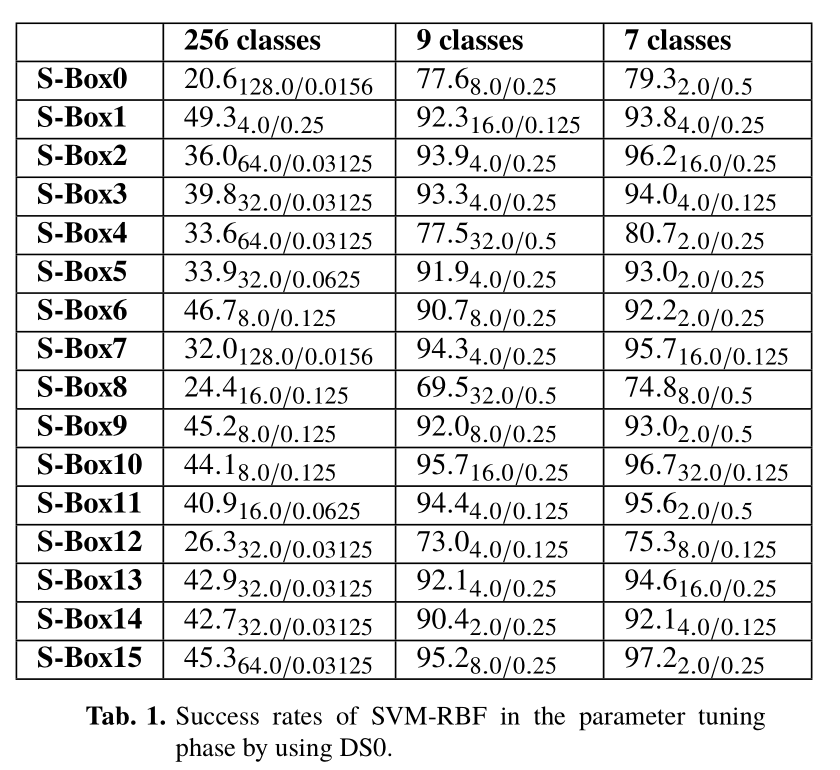
此外，32个相关度最高的样本瞬间被选为感兴趣点。如图3所示，对于第八个S-Box，大多数样本瞬间没有明显的功率泄漏。由于空间不足，我们省略了剩余S-Box的详细信息。在这里，我们仅使用皮尔逊相关法进行特征选择。此外，许多信号预处理技术也可用于在PA攻击中选择感兴趣的点，例如最小冗余最大相关性（mRMR）[25]和主成分分析（PCA）[26]等。

 

 

 

3.2 SMOTE

4.实验和结果

　　LIBSVM（支持向量机库）[30]被用作进行攻击的框架。所有实验均在华硕笔记本电脑上进行，该笔记本电脑采用2.50GHz Intel Core（TM）i5-7200U、16GB 2133MHz DDR4（Windows10 x64）。攻击持续了大约12周，没有考虑创建两个数据集的时间。

4.1参数调整阶段

　　在参数调整阶段，没有一种有效的学习方法来覆盖所有攻击场景。

　　根据论文[31]，我们选择了0.01至256的惩罚参数C，步长为2，ε（终止标准的容差）从0.01至0.25，步长0.05，（6）中的超参数γ从0.001至32，步长2。这里我们给出了参数范围，但省略了调整细节。一个开源的python工具箱，即不平衡学习[32]，被用来生成合成动力轨迹。[4000/8000]

 

 

 

 

 

 

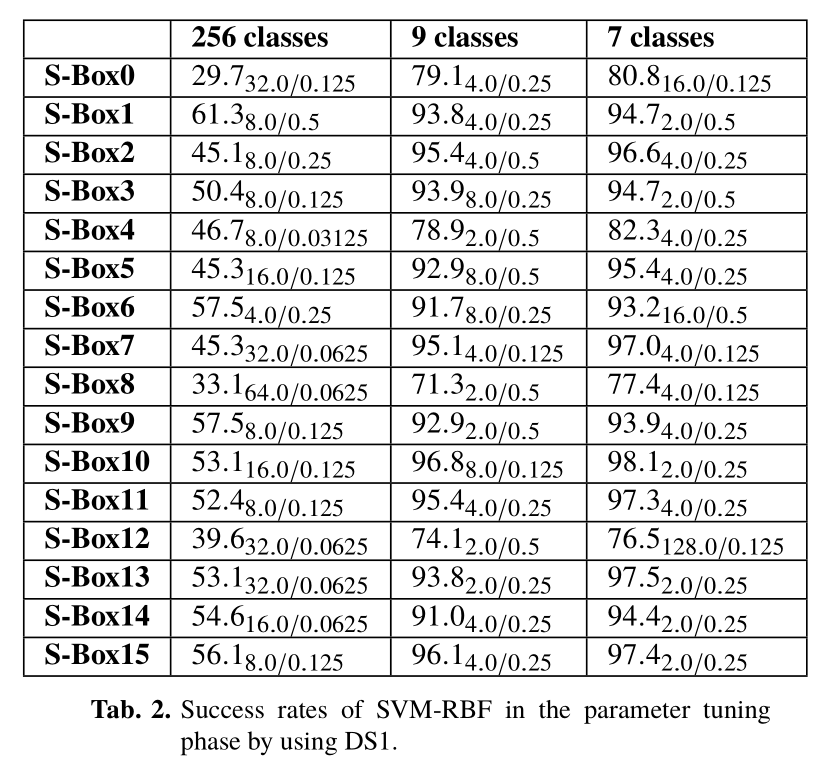
 　　在Tab.1和2，以ACC C/γ形式给出了所有S-Box的SVM-RBF的成功率。ACC的所有值以百分比形式给出，我们提供了达到这些值的参数组合惩罚参数C和超参数γ）。对于SVM-RBF，7个均匀分布类的成功率显著高于9个二项式类。这证明了分析轨迹的分布会影响SVM-RBF的性能。当数据集大小从DS0扩展到DS1时，9个二项式分布类的成功率提高了不到1.5%。令人兴奋的是，使用DS0的7个硬件类的成功率基本上等同于使用DS1的9个二项式类。换句话说，我们的方法在不增加配置跟踪数的情况下提高了SVMRBF的性能，这是PA攻击的一个有趣方面。

　　对于SVM-RBF，256个类的成功率明显低于7和9个类。这可以解释为这样一个事实，即分析跟踪的数量不足以训练好的参数来对256个类进行分类。然而，当考虑随机分类时，9个类有1/9的概率成功猜测，而256个类场景中有1/256的概率随机命中。显然，256节课的成功率高于随机猜测。甚至可以通过更详尽的参数调整阶段进一步改进结果，这需要更多的分析跟踪和更长的调整时间。然而，参数调整的复杂性使得很难对SVM的性能给出一些理论解释。此外，攻击方法的高复杂性使得所研究的算法在某些安全评估场景中没有吸引力。

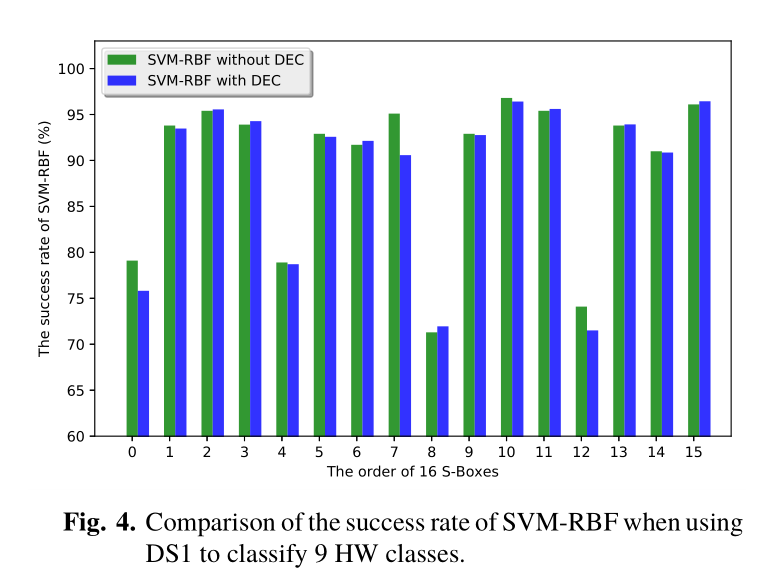
　　我们还使用SVM-RBF和DEC来解决数据不平衡引起的问题。图4给出了使用DS1对9个二项式分布式硬件类进行分类时，SVM-RBF与DEC的成功率。与使用相同成本相比，具有DEC的SVM-RBF的性能具有几乎没有改进，对于一些S-Box来说甚至更糟。原因可能是我们在第3.2节中描述的设置惩罚参数的策略不合适。然而，惩罚参数需要迭代计算，这在这个问题中很难设置。因此，在后续实验中，我们没有报告使用DEC方法的SVM结果。

4.2测试结果

　　在本节中，我们只报告了使用DS0和DS1时的SVM线性、SVM-RBF（具有最佳参数组合）和TA的结果。我们在独立测试集上进行了实验，以验证SVM和TA在分类7、9和256类时的性能。请注意，对于SVM和TA，我们使用了相同的数据集和相同的兴趣点。为了使实验结果准确，每个实验重复十次，然后将他们的平均分数作为最终结果。
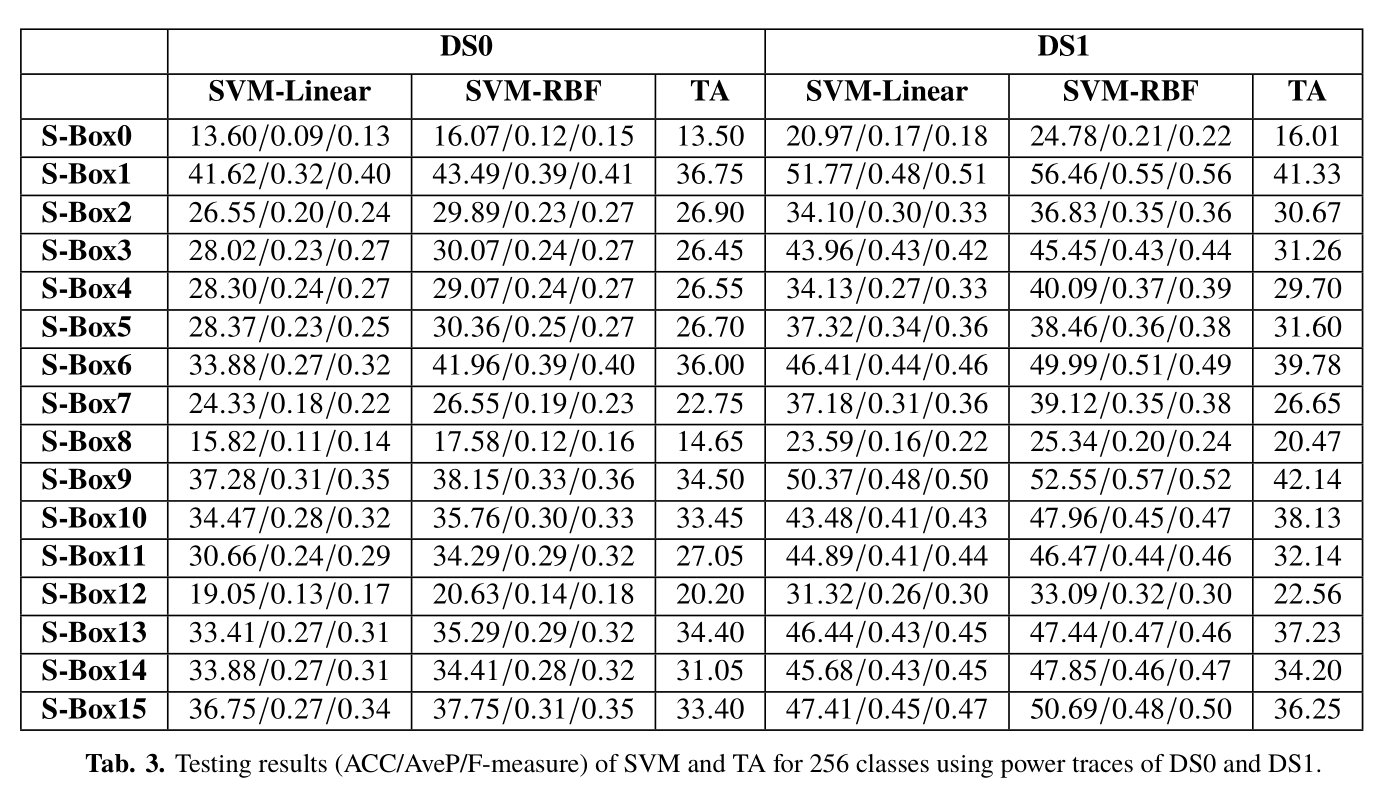
　　测试结果以SVM线性和SVM-RBF的ACC/AveP/F度量的形式给出，而对于TA，我们只给出了成功率。这里，F度量（F1分数）为准确度和召回率的调和平均值，其中准确度是真阳性与预测阳性的比率，而召回率是真阳性和实际阳性的比率[33]。接收机工作特性曲线通常用于表示具有均匀分布类的二进制分类问题的结果。然而，当处理高度倾斜的数据集时，精度召回曲线提供了关于学习算法性能的更多信息[34]。平均精度（AveP）定义为精度召回曲线下的面积。在选项卡中。3、4和5，ACC的所有值均以百分比表示，而AveP和F测量值在[0，1]范围内。值越高，结果越好。
　　正如预期的那样，由于SVM的泛化，SVM-RBF在参数调整阶段的成功率高于测试阶段的结果。对于256个类，SVM RBF的成功率通常降低3%至10%，在最坏的情况下，成功率从39.8%降至30.07%（见S-Box3，DS0，表3）。我们可以看到，对于16个S-Box，由于功耗泄漏信息的不同，SVM的成功率明显不同。当数据集大小从DS0扩展到DS1时，SVM的成功率提高了10%以上
适用于大多数S-Box。也就是说，数据集大小越大，成功率越高。原因是SVM的性能由其参数决定，数据集大小对参数优化至关重要。此外，SVM-RBF的成功率为1%∼ 当使用表3中的DS1时，比SVM Linear高6%
来自选项卡。4和5，我们可以看到，7个均匀分布类的测试结果比9个二项式类的测试效果要好得多。特别是，对于S-Box0、2、5、8、11和14，7个均匀分布类的成功率至少比9个二项式类高3%。对于SVM和TA，RADIOENGINEERING，第27卷，第1期，2018年4月295日，使用DS0的7个均匀分配类成功率高于使用DS1的9个二项式类，这是令人惊讶的结果。通常，随着轮廓轨迹数量的增加，SVM的性能得到了提高。
在这种情况下，SMOTE用于补偿现有学习集的分布。然而，SVM的成功率高于在训练阶段使用更多轮廓跟踪的成功率，这是因为对少数类使用了合成功率跟踪。这表明SVM的性能取决于属于每个类的轮廓跟踪数的分布。此外，核函数在提高SVM性能方面发挥着重要作用。SVM-RBF在分类7和9类时的成功率高于SVM-Linear。此外，使用DS0的SVM-RBF的成功率高于使用DS1的SVM线性。（6）中的超参数γ为SVM-RBF提供了更大的灵活性。不可避免地，SVM-RBF在参数调整阶段也需要更多的时间来找到最佳分离超平面。
尽管成功率给人的印象是SMOTE提高了SVM的性能，但AveP和F-measure可以从一个新的角度分析测试结果。9个HW类的平均值分布在0.68和0.95之间，而7个类的平均数分布在0.76和0.99之间，我们发现，当区分HW类0（或8）和另一类时，SVM分类器将所有实例处理为具有更多分析痕迹的类。自然，将所有实例分类为一个类不会成功，因为这不会泄露任何有关密钥的信息。表中256个统一分布类的平均值介于0.09和0.57之间。显著低于表中7、9级。这是因为在分类256个类时，分析跟踪的数量不足以训练高精度分类器。通常，ACC值越高，F测量值越高。
此外，F度量略低于ACC。因此，由于篇幅不足，我们不详细讨论F度量。
我们还使用了标准TA方法来比较在相同攻击场景下的成功率。从信息理论的角度来看，TA被认为是最强大的攻击技术，它假设每条轨迹的采样点遵循多元高斯分布。如选项卡所示。当使用DS0和DS1对7、9和256类进行分类时，TA的成功率明显低于SVM。与SVM相比，当轮廓轨迹不足以揭示关键相关泄漏信息时，TA的数值不稳定性突出。此外，随着分析迹线数量的增加，TA的成功率没有显著提高。然而，7个均匀分布类的TA成功率高于9个二项式类。简言之，我们的测试结果表明，使用SMOTE来补偿硬件类的分布对于TA也是有效的。此外，SVM（特别是SVMRBF）在正确使用时可以显著优于经典TA。
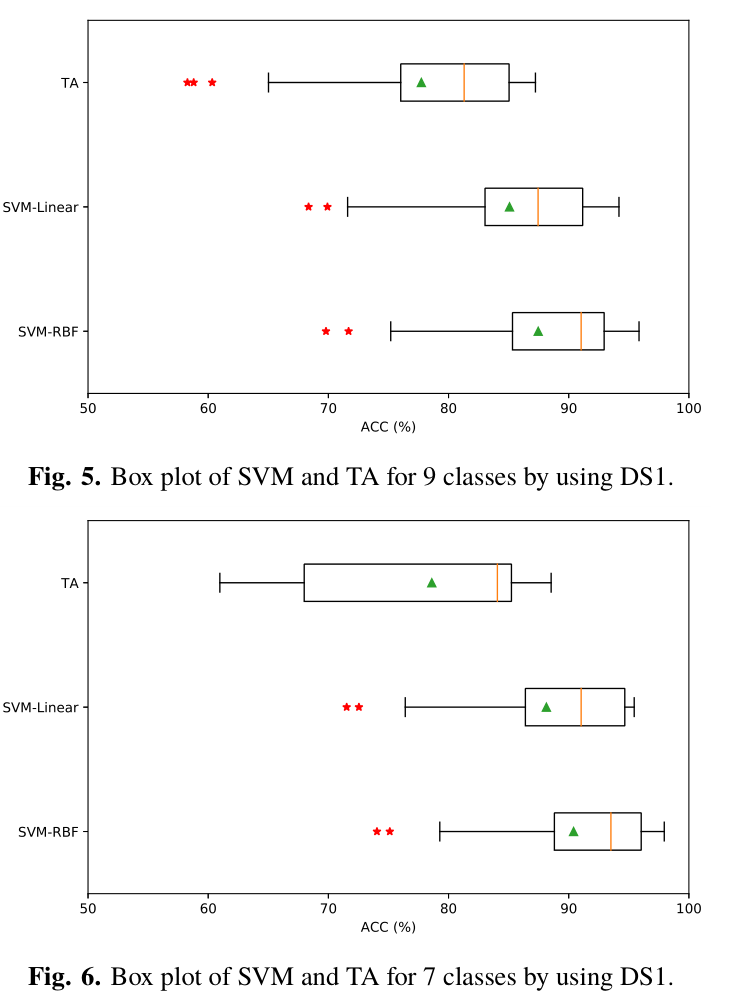
为了使我们的实验更有说服力，我们的攻击被执行了数百次，然后我们给出了成功率的统计结果。图5和6给出了一些方框图，总结了使用DS1对7类和9类进行分类时SVM和TA的成功率。在每个方框图中，中心条对应于中位数（第二个四分位数），绿色三角形代表平均值。盒子的底部和顶部始终是第一和第三个四分位数，胡须是最大/最小值，不包括异常值。当该值大于上/下四分位数的3 2倍时，视为异常值。与我们的假设一致，SMOTE可以有效地解决由数据不平衡引起的问题，这提高了SVM和TA的性能。此外，SVM（特别是SVM RBF）的成功率比TA更高、更集中。

 

 

5.结论

　　如上一节所述，PA攻击被认为是机器学习中的分类问题。SVM和TA创建特征（模板）来表征训练集的功率轨迹，然后计算这些特征与测试集的新轨迹之间的相似性。最终，结果提供了一定的概率。通常，TA假设功率迹线的采样点由一组有限正态分布近似。然而，ML算法假设样本点服从独立且相同的分布，但不限于特定的分布。因此，通过分析相同的兴趣点，SVM可以比TA提取更多关于秘密密钥的信息。
　　本文讨论了属于每个类的简档轨迹分布对支持向量机在PA攻击中性能的影响。SVM算法在不考虑轮廓轨迹分布的情况下优化了总体精度，而轮廓轨迹在高度倾斜的数据集上表现不佳。在对二项式分布式硬件类进行分类时，使用SMOTE来弥补这一不足。结果表明，在测试阶段，对于SVM和TA，7个均匀分布类的成功率高于9个二项式类。此外，具有适当参数的SVM的性能优于TA。当使用DS1对7个类进行分类时，SVM-RBF平均需要少于4个功率跟踪来恢复密钥。进一步分析表明，SMOTE在攻击有效性和效率方面显著提高了SVM的性能。

References