方差分析(Anova)
1.单因素方差分析：
单因素方差分析：只有一个因素A对实验指标有影响，假设因素A有r个水平，分别在第i个水平下进行多次独立的观察，所得到的实验指标数据如下：
A1：N(μ1,σ2) X11 X12 ... X1n1
A2：N(μ2,σ2) X21 X22 ... X2n2
Ar：N(μr,σ2) Xr1 Xr2 ... Xrnr
注意：每个水平的观测次数不一定一样
各总体间相互独立，因此有下面的模型：
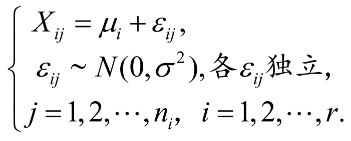
Xij就是第i个水平的第j个观测值，μi就是第i个水平的理论均值，εi显示随机误差（误差服从正态分布）
分析因素A对于实验指标是否有显著影响，可以看因素A不同水平的均值是否有显著差异，因此有如下假设：
原假设：H0:μ1=μ2=...μr
备选假设 H1：既是均值不全相等
Xij有偏差，要不就是由于不同水平的均值不同，又或者是随机误差的存在，因此全部Xij之间的差异的公式如下：
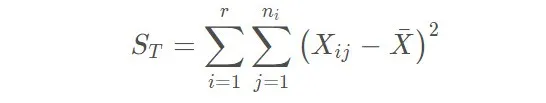
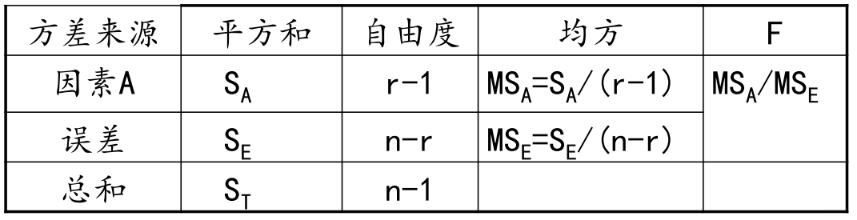
上面这个叫总偏差平方和
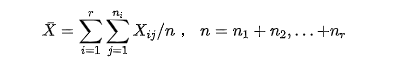
有A因素引起的 差异叫效应平方和SA （反应的是在因素A的不同水平下，样本均值和总体数据均值差异的平方和），随机误差引起的差异，叫做误差平方和SE （反应是在因素A的各个取值下，每组观察数据与这组数据均值的平方误差之和，反应的是随机误差的大小）
首先计算误差平方和 ，这样个体之间的差异的每个水平的均值没有关系，因此有如下：
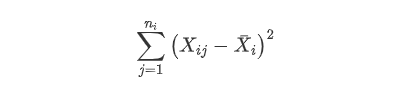
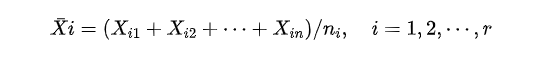
综合上述表达，得到：
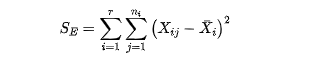
总偏差平方和减去误差平方和，得到
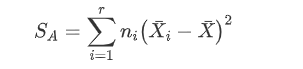
SE如果除以σ2则会符合自由度为ni-1的卡方分布
当H0为真的时候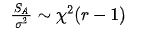
，但是我们不知道σ2，因此为了抵消这个未知量，我们构造的检验统计量为：
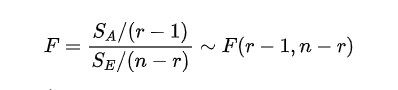
我们最终只会关系p值，如果p>0.05则接受原假设，否则拒绝原假设
例子：
import pandas as pd import numpy as np from scipy import stats from statsmodels.formula.api import ols from statsmodels.stats.anova import anova_lm # 这是那四个水平的索赔额的观测值 A1 = [1.6, 1.61, 1.65, 1.68, 1.7, 1.7, 1.78] A2 = [1.5, 1.64, 1.4, 1.7, 1.75] A3 = [1.6, 1.55, 1.6, 1.62, 1.64, 1.60, 1.74, 1.8] A4 = [1.51, 1.52, 1.53, 1.57, 1.64, 1.6] data = [A1, A2, A3, A4] # 方差的齐性检验 w, p = stats.levene(*data) if p < 0.05: print('方差齐性假设不成立') # 成立之后， 就可以进行单因素方差分析 f, p = stats.f_oneway(*data) print(f, p) # stats.f_oneway函数就可以直接算出检验假设的f值和p值
为什么要做方差记性检验：方差齐性检验是方差分析的重要前提，是方差可加性原则应用的一个条件
方差的齐性检验,如果p<0.05则拒绝原假设，即是方差不齐性
如果手动去计算：
#首先将数据改成DataFrame形式 values = A1.copy() groups = [] for i in range(1, len(data)): values.extend(data[i]) #extend() 函数用于在列表末尾一次性追加另一个序列中的多个值 for i, j in zip(range(4), data): groups.extend(np.repeat('A'+str(i+1), len(j)).tolist()) df = pd.DataFrame({'values': values, 'groups': groups}) #单因素分析 from statsmodels.formula.api import ols from statsmodels.stats.anova import anova_lm anova_res = anova_lm(ols('values~C(groups)', df).fit()) anova_res.columns = ['自由度', '平方和', '均方', 'F值', 'P值'] anova_res.index = ['因素A', '误差'] anova_res # 这种情况下看p值 >0.05 所以接受H0
2.双因素方差分析：
双因素方差分析和多因素方差分析在原理上是一致的，
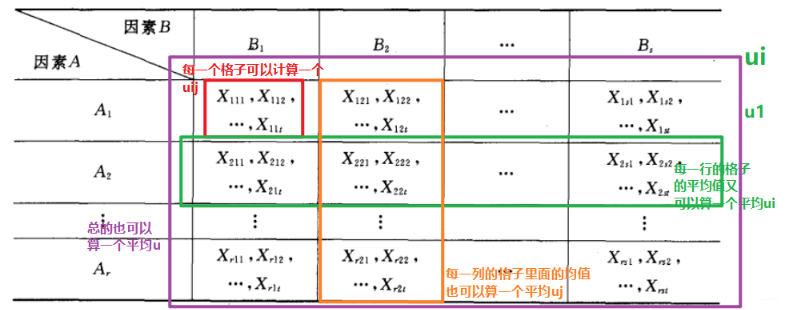
双因素方差分析就是在因素A,B作用下试验的指标，因素A有r个水平，因素B有s个水平，在A,B的不同水平下得到的试验结果如下：
并设有条件
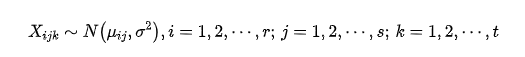
Xijk独立，数学模型如下：
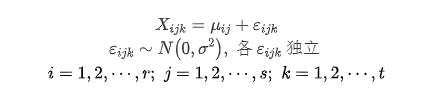
每一个格子都有一个平均值，每一行每一列也有平均值，这里先定义均值：
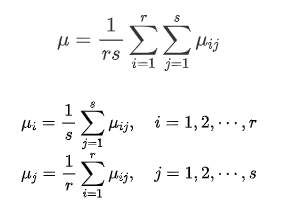
μ是总的均值，再定义两个公式：
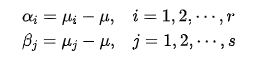
αi为水平Ai上的效应，βj为水平Bj的效应 ，很显然
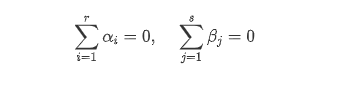
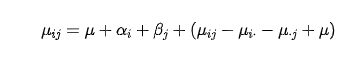
将其代入到前面的公式里面，得到;
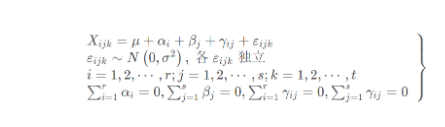
这个模型就会得到三个假设检验问题
因素A对于实验结果是否带来了显著效果
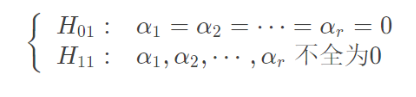
因素B对于实验结果是否带来了显著效果
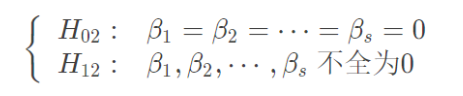
两者组合是否带来了显著效果
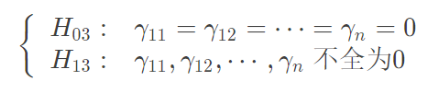
因素A的i水平和因素B的j水平的平均值;
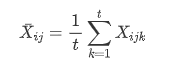
因素A的i水平上的平均值：
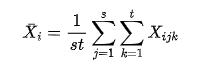
因素B的j水平均值：
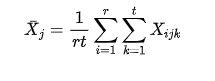
总的均值：
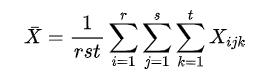
总偏差平方和：
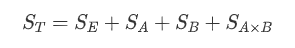
其中SE是误差平方和，SA和SB分别是因素A和B的效应平方和，SAxB是A和B的组合效应平方和
ST的自由度是rst-1，SE的自由度是rs(t-1)，SA的自由度是r-1，SB自由度是s-1
当H01为真时：
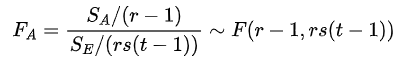
这时候取显著水平α，得到的拒绝域为：
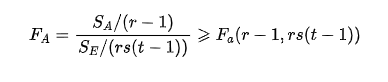
同理H02拒绝域为：
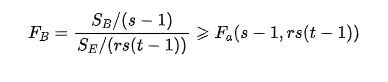
H03的拒绝域为：
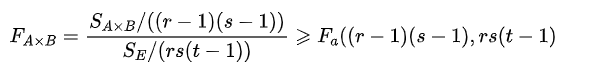
导入双因素分析使用到的包：
import pandas as pd import numpy as np from scipy import stats from statsmodels.formula.api import ols from statsmodels.stats.anova import anova_lm # 这三个交互效果的可视化画图 from statsmodels.graphics.api import interaction_plot import matplotlib.pyplot as plt from pylab import mpl # 显示中文 # 这个看某个因素各个水平之间的差异 from statsmodels.stats.multicomp import pairwise_tukeyhsd
2.1无交互作用的情况：即是对每一个组合因素只进行一次独立实验，每一格只有一个值，称为无重复实验
下面进行双因素方差分析，简要流程是，先用pandas库的DataFrame数据结构来构造输入数据格式。然后用statsmodels库中的ols函数得到最小二乘线性回归模型。最后用statsmodels库中的anova_lm函数进行方差分析
#导入数据 dic_t2=[{'广告':'A1','价格':'B1','销量':276},{'广告':'A1','价格':'B2','销量':352}, {'广告':'A1','价格':'B3','销量':178},{'广告':'A1','价格':'B4','销量':295}, {'广告':'A1','价格':'B5','销量':273},{'广告':'A2','价格':'B1','销量':114}, {'广告':'A2','价格':'B2','销量':176},{'广告':'A2','价格':'B3','销量':102}, {'广告':'A2','价格':'B4','销量':155},{'广告':'A2','价格':'B5','销量':128}, {'广告':'A3','价格':'B1','销量':364},{'广告':'A3','价格':'B2','销量':547}, {'广告':'A3','价格':'B3','销量':288},{'广告':'A3','价格':'B4','销量':392}, {'广告':'A3','价格':'B5','销量':378}] df_t2=pd.DataFrame(dic_t2,columns=['广告','价格','销量'])
进行方差分析
# 方差分析 price_lm = ols('销量~C(广告)+C(价格)', data=df_t2).fit() table = sm.stats.anova_lm(price_lm, typ=2)
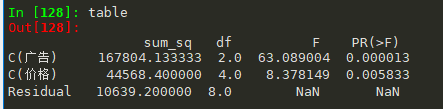
即是不同价格和广告都会对销量有显著差异
fig = interaction_plot(df_t2['广告'],df_t2['价格'], df_t2['销量'], ylabel='销量', xlabel='广告')
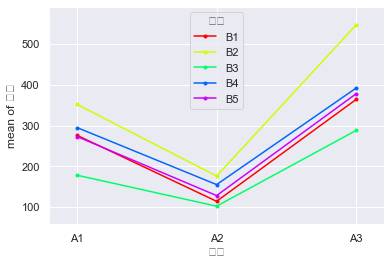
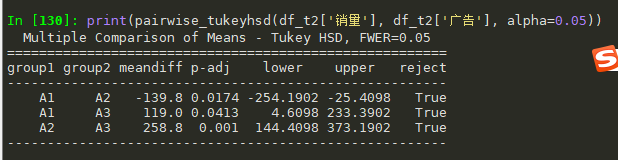
# 广告与销量的影响 print(pairwise_tukeyhsd(df_t2['销量'], df_t2['广告'], alpha=0.05)) # 第一个必须是销量， 也就是我们的指标
2.2有交互作用的情况：
即是每个格子有不止一个值，也称为重复试验
#先构造数据 dic_t3=[{'燃料':'A1','推进器':'B1','射程':58.2},{'燃料':'A1','推进器':'B1','射程':52.6}, {'燃料':'A1','推进器':'B2','射程':56.2},{'燃料':'A1','推进器':'B2','射程':41.2}, {'燃料':'A1','推进器':'B3','射程':65.3},{'燃料':'A1','推进器':'B3','射程':60.8}, {'燃料':'A2','推进器':'B1','射程':49.1},{'燃料':'A2','推进器':'B1','射程':42.8}, {'燃料':'A2','推进器':'B2','射程':54.1},{'燃料':'A2','推进器':'B2','射程':50.5}, {'燃料':'A2','推进器':'B3','射程':51.6},{'燃料':'A2','推进器':'B3','射程':48.4}, {'燃料':'A3','推进器':'B1','射程':60.1},{'燃料':'A3','推进器':'B1','射程':58.3}, {'燃料':'A3','推进器':'B2','射程':70.9},{'燃料':'A3','推进器':'B2','射程':73.2}, {'燃料':'A3','推进器':'B3','射程':39.2},{'燃料':'A3','推进器':'B3','射程':40.7}, {'燃料':'A4','推进器':'B1','射程':75.8},{'燃料':'A4','推进器':'B1','射程':71.5}, {'燃料':'A4','推进器':'B2','射程':58.2},{'燃料':'A4','推进器':'B2','射程':51.0}, {'燃料':'A4','推进器':'B3','射程':48.7},{'燃料':'A4','推进器':'B3','射程':41.4},] df_t3=pd.DataFrame(dic_t3,columns=['燃料','推进器','射程'])
#方差分析 moore_lm = ols('射程~燃料+推进器+燃料:推进器', data=df_t3).fit() table = sm.stats.anova_lm(moore_lm, typ=1)
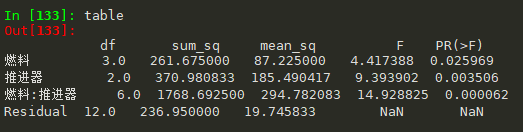
fig = interaction_plot(df_t3['燃料'],df_t3['推进器'], df_t3['射程'], ylabel='射程', xlabel='燃料')
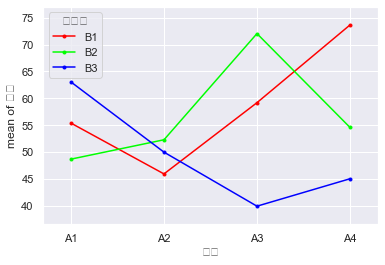
从这个图里面可以看出， (A4, B1)和(A3, B2)组合的进程最好
print(pairwise_tukeyhsd(df_t3['射程'], df_t3['燃料']))
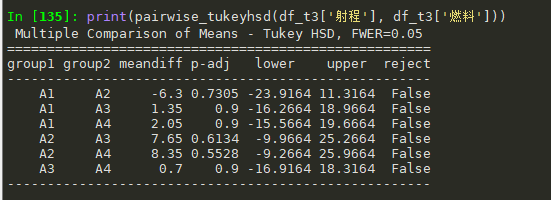
都是False， 说明A因素各个水平之间无显著差异
print(pairwise_tukeyhsd(df_t3['射程'], df_t3['推进器']))
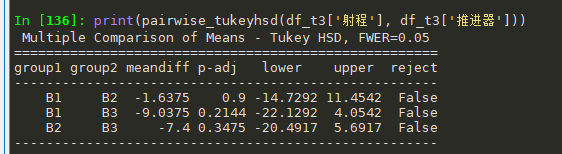
B也没有差异
